
- •Математика
- •Пересечение множеств
- •Вычитание множеств
- •Свойства операций над множествами
- •Число элементов в объединении конечных множеств и в дополнении к подмножеству
- •Контрольные вопросы:
- •Способы задания декартова произведения двух множеств
- •Основные свойства декартова произведения.
- •Раздел II. Элементы комбинаторики
- •Контрольные вопросы:
- •Контрольные вопросы:
- •Перестановки без повторений
- •Бином Ньютона
- •Свойства сочетаний. Треугольник Паскаля.
- •1. Правило симметрии:
- •Раздел III. Математические утверждения и их структура
- •Контрольные вопросы:
- •Отношения между понятиями
- •Способы определения понятий
- •Требования к определению понятий
- •Контрольные вопросы:
- •Высказывания и операции над ними
- •Операции над высказываниями
- •Отрицание высказываний
- •Законы отрицания:
- •Конъюнкция двух высказываний
- •Импликация высказываний
- •Закон контрапозиции
- •Эквиваленция двух высказываний
- •Обращение предиката в высказывание
- •Операции над предикатами
- •Отрицание высказываний, содержащих кванторы
- •Отношение логического следования и равносильности на множестве предложений
- •Строение теоремы. Виды теорем
- •Закон контрапозиции. Теоремы
- •Умозаключения. Анализ рассуждений. Простейшие правила вывода
- •Простейшие схемы дедуктивных умозаключений
- •Способы установления истинности умозаключения
- •Индуктивные умозаключения
- •Раздел IV. Соответствия
- •Контрольные вопросы:
- •Полный образ и полный прообраз
- •Способы задания соответствий
- •Типы соответствий
- •Отображения
- •Виды отображений
- •Отношения
- •Свойства отношений на множестве
Свойства операций над множествами
Операции объединения, пересечения, разности множеств обладают следующими свойствами:
1.
Коммутативность объединения: А![]() В
= В
В
= В![]() А
А
пересечения:
A![]() B
= В
B
= В![]() А
А
2.
Ассоциативность объединения: (А![]() В)
В)
![]() С
= А
С
= А![]() (В
(В
![]() С)
С)
пересечения:
(A![]() B)
B)
![]() С
= A
С
= A![]() (B
(B![]() С)
С)
3. Дистрибутивность объединения относительно пересечения:
А![]() (B
(B![]() С)
= (А
С)
= (А В)
В)
![]() (А
(А![]() С)
С)
или
(A![]() B)
B)
![]() С
= (А
С
= (А![]() С)
С)
![]() (В
(В![]() С)
С)
пересечения относительно объединения:
A![]() (В
(В
![]() С)
= (A
С)
= (A![]() B)
B)
![]() (А
(А![]() С)
С)
или
(А![]() В)
В)
![]() С
= (A
С
= (A![]() С)
С)
![]() (B
(B![]() С)
С)
4.
Идемпотентность объединения: А![]() А=
А
А=
А
пересечения:
A![]() А
= А
А
= А
5.
Поглощения объединения: А![]() J
= J
и А
J
= J
и А![]() Ø
= А
Ø
= А
пересечения:
A![]() J
= А
и А
J
= А
и А Ø
= Ø
Ø
= Ø
6.
Если А![]() В,
то А
В,
то А![]() В
= В и A
В
= В и A![]() B
= А
B
= А
7.
А![]() (А
(А![]() В)
= А
и A
В)
= А
и A![]() (А
(А![]() В)
= А
В)
= А
8.
Законы де Моргана: (А В)
В)![]() =
A
=
A![]()
![]() B
B![]()
(A![]() B)
B)![]() = A
= A![]()
![]() В
В![]()
9.
![]()
![]()
10.
Закон двойного отрицания:
![]()
11.
![]() J
J
![]() Ø
Ø
12.
![]() .
.
Законы
алгебры множеств по отношению к операциям
пересечения и объединения подчиняются
принципу
двойственности:
если в любом верном тождестве знаки
пересечения заменить знаками объединения,
а все знаки объединения заменить знаками
пересечения (![]() ),
знак универсального множества заменить
знаком пустого множества, а знак пустого
– знаком универсального множества
),
знак универсального множества заменить
знаком пустого множества, а знак пустого
– знаком универсального множества
![]() Ø,
то получим также верное равенство.
Ø,
то получим также верное равенство.
Например,
![]() - верное равенство. Тогда в силу принципа
двойственности
- верное равенство. Тогда в силу принципа
двойственности
![]() Ø
– также верное равенство.
Ø
– также верное равенство.
Доказательство некоторых свойств операций объединения и пересечения прямо следует из их определения, доказательство других свойств также можно провести.
Самостоятельно рассмотреть понятие пересечения, объединения «п» множеств.
Число элементов в объединении конечных множеств и в дополнении к подмножеству
Пусть
А
и В
– два непустых конечных множества.
Число элементов во множестве будем
обозначать
![]() или
или
![]() .
Например, если А
=
{a;b;c;d},
В
=
{m;n},
то
.
Например, если А
=
{a;b;c;d},
В
=
{m;n},
то
![]() = 4, а
= 4, а
![]() = 2.
= 2.
Теорема: Число элементов в объединении двух конечных множеств равно сумме чисел элементов в каждом из них, уменьшенной на число элементов в их пересечении.
![]()
![]()
Доказательство:
Обозначим
число элементов во множестве
![]() буквой
буквой
![]() ,
а во множестве
,
а во множестве
![]() буквой
буквой
![]() ,
т.е.
,
т.е.
![]() .
.
1 B A

![]() Ø.
Тогда
Ø.
Тогда
![]() и формула примет вид:
и формула примет вид:
![]() .
.
![]()
Штриховкой
на диаграмме показано
![]() .
Очевидно, что
.
Очевидно, что
![]() .
.
A B


2)
Пусть
![]() Ø.
Ø.
![]()
![]()
![]() на
диаграмме показано двойной штриховкой.
Так как множества
А
и
В –
конечные множества и
на
диаграмме показано двойной штриховкой.
Так как множества
А
и
В –
конечные множества и
![]() Ø,
то
Ø,
то
![]() также множество конечное. Пусть n(
также множество конечное. Пусть n(![]() )= c,
)= c,
![]() .
.
Очевидно,
что
![]() состоит из трех
попарно непересекающихся
подмножеств:
состоит из трех
попарно непересекающихся
подмножеств:
![]() (на диаграмме показано двойной штриховкой),
(на диаграмме показано двойной штриховкой),
![]() (на
диаграмме показано горизонтальной
штриховкой),
(на
диаграмме показано горизонтальной
штриховкой),
![]() (на диаграмме показано вертикальной
штриховкой). Тогда
(на диаграмме показано вертикальной
штриховкой). Тогда
![]() =
=
![]() +
+
![]() +
+
![]() (смотри случай 1).
(смотри случай 1).
Пусть
![]() =
=![]() ,
,
![]() =
=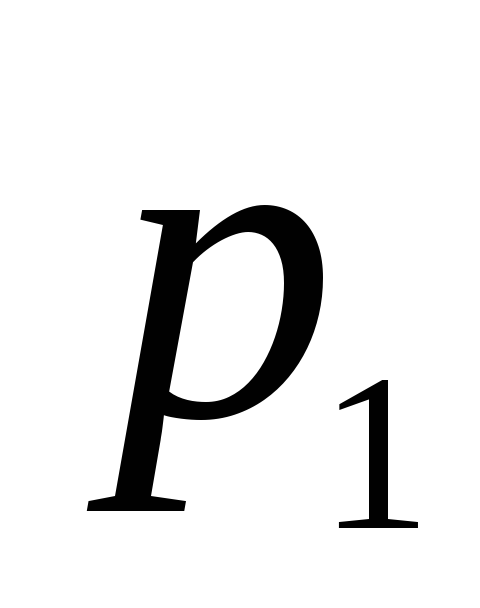 .
Тогда
.
Тогда
![]() =
=
![]() +c+
+c+![]() =(
=(![]() +c)+
+c)+ =
(
=
( +c)+
+c)+ +c
- c
= (
+c
- c
= (![]() +c)+(
+c)+(![]() +c)
– c
= m
+ p
– c
=
+c)
– c
= m
+ p
– c
=
![]() .
.
Теорема: Число элементов в объединении трех конечных множеств А, В, С, равно:
![]() Доказательство:
Доказательство:
В
основе доказательства лежит свойство
ассоциативности операции объединения
множеств:
![]() А также тот факт, что равные множества
состоят из одних и тех же элементов.
Тогда
А также тот факт, что равные множества
состоят из одних и тех же элементов.
Тогда
![]() .
Доказать сам-но.
.
Доказать сам-но.
Теорема: Пусть даны конечные множества А и В. И пусть В – собственное подмножество множества А. Тогда n(A \ B) = n(A)-n(B).
Доказательство
Пусть
даны множества А
и
В,
где
![]() .
Тогда
.
Тогда
![]() ,
и
,
и
![]() Ø.
Тогда
Ø.
Тогда
![]() .
Отсюда
.
Отсюда
![]() .
.
Так
как
![]() ,
то
,
то
![]() ,
где
,
где
![]() .
.
Лекция № 6. ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ.
