ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Факультет прикладной математики и информационных технологий Кафедра высшей математики

С.Л.Рычков

ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

Учебное пособие

Специальность 1003.00 — «Электроснабжение»

Киров 2006

УДК 517.2

Рецензент:

д.ф.-м.н., проф. каф. ММЭ Шатров А.В.

Элементы теории функций комплексного переменного. Учебное пособие: спец. 1003.00/ С.Л.Рычков. — Киров, 2006. — 111 с.

Приводятся теоретические сведения, необходимые для понимания сущности методов ТФКП, применяемых в прикладных электротехнических дисциплинах.

Авторская редакция.

c Рычков Сергей Леонидович, 2006.

c Вятский государственный университет, 2006.

Оглавление

1 Лекция 1		7
1.1	Основные определения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	7
1.2	Последовательности комплексных чисел. Бесконечно удаленная точка. . . . . .	8

1.3Предел функции комплексной переменной. . . . . . . . . . . . . . . . . . . . . . 10

1.4Непрерывность функций комплексной переменной. . . . . . . . . . . . . . . . . 10

1.5Аналитические функции. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

2 Лекция 2

15

2.1Интеграл от функции комплексного переменного. . . . . . . . . . . . . . . . . . 15

2.2 Свойства интеграла. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

2.3Теорема Коши. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

2.4Неопределенный интеграл. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

2.5 Интеграл Коши. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

2.6Производные аналитической функции. . . . . . . . . . . . . . . . . . . . . . . . . 22

3 Лекция 3

25

3.1Ряды с комплексными членами. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25

3.2Функциональные ряды. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

3.3Свойства равномерно сходящихся рядов. . . . . . . . . . . . . . . . . . . . . . . 27

3.4Степенные ряды. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

3.5Ряд Тейлора. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

3.6Единственность определения аналитической функции. . . . . . . . . . . . . . . 32

4 Лекция 4

35

4.1Аналитическое продолжение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35

4.1.1Продолжение с действительной оси. . . . . . . . . . . . . . . . . . . . . . 35

4.1.2Продолжение соотношений. . . . . . . . . . . . . . . . . . . . . . . . . . . 36

4.1.3Аналитическое продолжение через границу. . . . . . . . . . . . . . . . . . 38

4.1.4Аналитическое продолжение при помощи степенных рядов. . . . . . . . 38

4.2Правильные и особые точки аналитической функции. . . . . . . . . . . . . . . . 40

4.3Понятия римановой поверхности и полной аналитической функции. . . . . . . 41

5 Лекция 5

43

5.1Ряд Лорана. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43

5.2Классификация изолированных особых точек. . . . . . . . . . . . . . . . . . . . 45

5.2.1Устранимая особая точка. . . . . . . . . . . . . . . . . . . . . . . . . . . . 46

5.2.2Полюс порядка m. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46

5.2.3Существенно особая точка. . . . . . . . . . . . . . . . . . . . . . . . . . . 47

3

5.3 Бесконечно удаленная точка как изолированная особая точка . . . . . . . . . .	48
6 Лекция 6	51

6.1Вычет аналитической функциив изолированной особой точке. . . . . . . . . . . 51

6.2Основная теорема теории вычетов. . . . . . . . . . . . . . . . . . . . . . . . . . . 52

6.3Вычисление определенных интеграловс помощью вычетов. . . . . . . . . . . . . 54

2π

6.3.1 Интегралы вида R(cos ϕ, sin ϕ) dϕ. . . . . . . . . . . . . . . . . . . . . . 54

0

∞

6.3.2Интегралы вида f (x) dx. . . . . . . . . . . . . . . . . . . . . . . . . . . 55

	−∞
6.3.3 Интегралы вида	∞	57
	ei axf (x) dx. . . . . . . . . . . . . . . . . . . . . . . . .
	−∞
7 Лекция 7		61
7.1 Преобразование Лапласа. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		61

7.2Изображения элементарных функций. . . . . . . . . . . . . . . . . . . . . . . . . 62

7.3Свойства преобразования Лапласа. . . . . . . . . . . . . . . . . . . . . . . . . . . 63

7.3.1 Свойство линейности. . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . 63

7.3.2Теорема подобия. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64

7.3.3Теорема запаздывания. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64

7.3.4Теорема смещения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65

7.3.5Дифференцирование оригинала. . . . . . . . . . . . . . . . . . . . . . . . 65

7.3.6Интегрирование оригинала. . . . . . . . . . . . . . . . . . . . . . . . . . . 66

7.3.7Дифференцирование изображения. . . . . . . . . . . . . . . . . . . . . . . 66

7.3.8Интегрирование изображения. . . . . . . . . . . . . . . . . . . . . . . . . 67

7.3.9Изображение свертки. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67

7.3.10Интеграл Дюамеля. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68

8 Лекция 8

71

8.1Обратное преобразование Лапласа. . . . . . . . . . . . . . . . . . . . . . . . . . . 71

9 Лекция 9

77

9.1Операционное исчисление. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77

9.2Сводка формул для преобразования Лапласа. . . . . . . . . . . . . . . . . . . . 78

9.3Примеры применения операторного метода . . . . . . . . . . . . . . . . . . . . . 80

A Элементарные функции.		87
A.1	Линейная функция. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	87
A.2	Обратно-пропорциональная зависимость. . . . . . . . . . . . . . . . . . . . . . .	87
A.3	Степенная функция. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	88
A.4	Показательная функция. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	92
A.5	Логарифмическая функция. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	94
A.6	Степенная функция общего вида. . . . . . . . . . . . . . . . . . . . . . . . . . . .	97
A.7	Тригонометрические и гиперболические функции. . . . . . . . . . . . . . . . . .	97
A.8	Обратные тригонометрические и гиперболические функции. . . . . . . . . . . .	108

4

В учебном пособии рассмотрена теория функций комплексного переменного в минимальном объеме, необходимом для осознанного освоения методов теории электрических цепей и понимания теоретических основ операционного исчисления.

По данному разделу математики есть много прекрасных учебников и пособий, однако, как показывает опыт, малодоступность некоторых изданий и довольно значительный объем изложенного препятствует усвоению материала студентами. С другой стороны, недостаток аудиторного времени не позволяет достаточно глубоко рассмотреть эти вопросы на лекциях. Настоящим предпринята попытка преодолеть названные трудности.

Пособие является в основном компендиумом из приведенной в списке литературы и может рассматриваться как расширенный конспект лекций, читаемых студентам электротехнического факультета Вятского государственного университета.

5

6

Лекция 1

1.1Основные определения.

Пусть мы имеем комплексные числа z = x + i y; z C . Как нам известно, все множество комплексных чисел может быть представлено точками комплексной плоскости Z .

Перенесем на плоскость Z понятия, определенные нами для плоскости двух действительных переменных — x и y; напомним некоторые из них.

Назовем δ-окрестностью точки z0 внутренность круга радиуса δ с центром в точке z0, определяемую неравенством: |z − z0| < δ.

Областью D называем множество точек плоскости, обладающее свойствами открытости и связности. Граничной точкой области называем точку, в любой окрестности которой находятся как точки D, так и не принадлежащие D. Граница области — совокупность всех граничных точек области D. Область D с присоединенной границей ее называется замкнутой областью D. Также будем различать односвязные и многосвязные области.

Определение 1.1 Говорят, что на множестве M плоскости Z задана функция w = f (z), если указан закон, по которому z M ставится в соответствие одна или несколько точек w комплексной плоскости W.

В первом случае функция f (z) называется однозначной, во втором — многозначной.

Множество M называется множеством определения функции f (z), а совокупность N всех значений w = f (z) называется множеством изменения (значений) функции f (z).

Наиболее важен случай, когда и M, и N представляют собой области комплексных плоскостей Z и W соответственно.

Обычно полагают z = x+i y, а w = u+i v, где x = Re z, y = Im z, u = Re w, v = Im w (Re z и Im z обозначают действительную и мнимую части комплексного числа z соответственно),

тогда	v = v(x, y)	(1.1)
w = f (z)
	u = u(x, y)

таким образом, задание одной функции комплексного переменного эквивалентно заданию двух функций двух действительных переменных.

Наличие четырех действительных переменных в комплексной функции одного комплексного переменного затрудняет наглядное графическое представление такой зависимости. Нельзя изобразить нечто простое и подобное графику функции одного действительного переменного. Есть несколько путей решения этой проблемы. Возможно построение по отдельности рельефов u = u(x, y) и v = v(x, y) как функций двух действительных переменных x и y, но чаще строят рельефы |f (z)| и arg f (z) как функций от x и y. Обычно рельеф изображается линиями уровня на плоскости XY , возможно и представление его в виде трехмерного образа.

7

С другой стороны, связь четырех действительных переменных выражается зависимостью между двумя комплексными переменными. Именно поэтому теория функций комплексного переменного облегчает решение многих задач математического анализа и прикладных дисциплин.

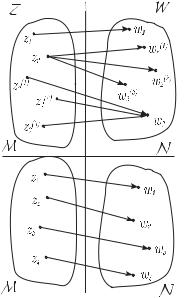
Возможно также представить функцию w = f (z) как отображение множества M комплексной плоскости Z на множество N комплексной плоскости W, как это иллюстрируется рисунком 1.1.

								f
				w = f (z), z M, w N : z → w.
				Если w = f (z) — однозначна на M и разным значени-
				ям z1 и z2 всегда соответствуют разные значения w1
				и w2, то это взаимно-однозначное отображение, ина-
				че называемое однолистным (смысл такого определе-
				ния станет понятен в дальнейшем), функция w = f (z)
				также называется тогда однолистной. Такой случай
				представлен в нижней части рисунка 1.1.
				Пусть w = f (z) — однолистная,
				f	, но можно задать обратное отображение:
				ϕ
				M −→ N
				M ←− N, тогда z = ϕ(w) — обратная функция , если
				w ≡ f (ϕ(w)).
				Приведем простой пример: пусть w = f (z) = az + b,
				где a и b — комплексные константы и a = 0, очевид-
				но, w — однозначная функция от z, но и z = ϕ(w) =
				= (w−b)/a — однозначна, так что f (z) — однолистная
				функция. Приведенные w = f (z) и z = ϕ(w) являют-
				ся парой взаимно-обратных линейных функций.
				Итак, нами установлено:						w = f (z)
		Рис. 1.1:		w = f (z) — однолистная						z = ϕ(w)
	— однозначные функции.									(1.2)
	Пусть w = f (z) отображает из			f		в		, а t	= g(w) отображает из
			Z	M −→ N			W				W
	g
	N −→ P	в T , тогда t = h(z) = g(f (z)) — называется сложной функцией, составленной из

функций f и g, или суперпозицией данных отображений.

1.2Последовательности комплексных чисел. Бесконечно удаленная точка.

Рассмотрим последовательность комплексных чисел или точек на комплексной плоскости:

zn = xn + i yn.

Задание последовательности {zn} эквивалентно заданию двух последовательностей действительных чисел: {xn} и {yn}.

Определение 1.2 Пределом последовательности {zn} называется комплексное число z, если для любого положительного числа ε найдется такое натуральное N , что для любого члена последовательности с номером n > N будет справедливо неравенство:

|z − zn| < ε.	(1.3)
Иначе говоря, nlim zn = z, если ε > 0 N : n > N	= |z − zn| < ε.
→∞

8

Рис. 1.2:

Очевидно также следующее:		n→∞ xn = x	(1.4)
nlim zn = z = x + i y
		lim
→∞		nlim yn = y
		→∞

Определение 1.3 Последовательность {zn} называется ограниченной, если на плоскости Z найдется круг конечного радиуса, внутри которого лежат все точки последовательно-

сти, то есть, если M > 0 : n = |zn| < M.

Последовательность {zn} называется неограниченно нарастающей в противном случае, то есть, если R > 0 N : n > N = |zn| > R.

Для единообразия формулировок вводится понятие бесконечно удаленной точки: z = ∞,

тогда для неограниченно нарастающей последовательности lim zn = ∞, а также можно записывать z −→ ∞. n→∞

Аргумент бесконечно удаленной точки не определен.

Определение 1.4 Полной комплексной плоскостью называется совокупность обычной комплексной плоскости и бесконечно удаленной точки.

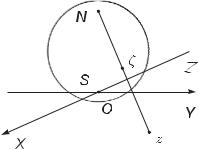
Можно дать такую геометрическую интерпретацию сказанному. Установим на комплексной плоскости Z сферу южным полюсом в точку (0,0), соединим произвольную точку плоскости z = 0 с север-

ным полюсом сферы отрезком прямой, как это показано на рисунке 1.2. Этот отрезок пересекает сферу в единственной точке ζ, которая будет являться об-

разом точки z или ее стереографической проекцией. Если сейчас устремить точку z в любом направлении

в сторону от точки z = 0, то ее стереографическая проекция ζ будет приближаться к северному полюсу сферы, который и является образом бесконечно удаленной точки. Ясно, что вся сфера целиком отображает полную комплексную плоскость.

Отметим следующие алгебраические свойства: Пусть {zn} −→ ∞, тогда {1/zn} −→ 0,

наоборот, если {ζn} −→ 0 и ζn = 0, то {1/ζn} −→ ∞. Величина ζn в таком случае называется бесконечно малой.

Условно это обозначается следующим образом (подразумевая соответствующие последо-

вательности):
1		= 0	1		= ∞
			и			(1.5)
	∞			0
z · ∞ = ∞			(если z = 0)			(1.6)
z/∞ = 0			(если z = ∞)			(1.7)
z + ∞ = ∞.						(1.8)

9

z→z0

1.3Предел функции комплексной переменной.

Пусть задана однозначная функция w = f (z) в окрестности точки z0 = x0 + i y0, кроме, возможно, как в самой точке z0.

Определение 1.5 Говорят, что существует предел lim f (z), если независимо от способа

			z→z0			lim v(x, y) = v
			lim u(x, y) = u		0			,
стремления x −→ x0 и y −→ y0 существуют пределы x→x0						и x→x0	0
при этом полагают			y→y0			y→y0
lim		+ i v0	= w0.				(1.9)
	f (z) = u0
z→z0
Иначе:
lim				= |f (z) − w0| < ε.
z z0 f (z) ε > 0 δ > 0 : 0 < |z − z0| < δ
→

Из такого определения и свойств пределов функций действительной переменной вытекают

следующие свойства:

lim (f

±

g) =

lim f

lim g;

lim (f

·

g) = lim f

lim g;

→

→

→

→

→

→

z z0

z z0

± z z0

z z0

z z0

· z z0

f

lim f

lim

=

z→z0

(g = 0,

lim

lim

z

→

z0

g

g

z z0 g = 0).

→

z→z0

В приведенных формулах подразумевается существование всех входящих в них пределов.

1.4Непрерывность функций комплексной переменной.

Определение 1.6 Однозначная функция w = f (z) называется непрерывной в z = z0, если она определена в самой z0 и некоторой ее окрестности и lim f (z) = f (z0).

Очевидно:
		u(x, y)			— непрерывны
f (z)— непрерывна в z0 = x0 + i y0		v(x, y)			в (x0, y0)	(1.10)
Отсюда следуют аналоги свойств непрерывных функций действительной переменной:
f (z) и g(z) — непрерывны = f (z) ± g(z);	f (z) · g(z);		f (z)		(g(z) = 0) — непрерывны.
			g(z)

Если f (z) непрерывна на замкнутом ограниченном множестве M (т.е. множестве, которое может поместиться в круге конечного радиуса R), тогда аналогично функциям действительной переменной:

1)она ограничена, т.е. |f (z)| < K, где K > 0 — некоторое конечное действительное число;

2)z1 и z2 M : z M = |f (z1)| |f (z)| и |f (z2)| |f (z)|, т.е.

|f (z)| достигает на M своего минимального и максимального значений; 3) f (z) — равномерно непрерывна на M , т.е.

ε > 0 δ > 0 : |z1 − z2| < δ = |f (z1) − f (z2)| < ε для z1 и z2 M.

Теорема 1.1 Если f (z) непрерывна в области D плоскости Z и взаимно-однозначно отображает D на множество в плоскости W, то — тоже область, и обратная функция z = ϕ(w) непрерывна в .

Данная теорема принимается без доказательства.

10