30.Координаты центров тяжести однородных тел

Для однородного тела вес любой его части пропорционален объему этой части: всего тела пропорционален объему V этого тела, т. е. где у — вес единицы объема.Подставив эти значения в формулы (59), заметим, что во всех суммах у как общий множитель выносится за скобки и сокращается с у в знаменателе.

В результате из формул (59) получим:

Как видно, положение центра тяжести однородного тела зависит только от его геометрической формы, а от величины у не зависит. По этой причине точку С, координаты которой определяются формулами (60), называют центром тяжести объема V.

Путем аналогичных рассуждений легко найти, что если тело представляет собой однородную плоскую и тонкую пластину, то для нее

(61)

где L — площадь всей пластины; — площади ее частей.

Точку, координаты которой определяются формулами (61), называют центром тяжести площади 

Точно так же получаются формулы для координат центра тяжести линии:

где L — длина всей линии; — длины ее частей.

По формулам (62) можно находить центры тяжести изделий из тонкой проволоки постоянного сечения.

Таким образом, центр тяжести однородного тела определяется, как центр тяжести соответствующего объема, площади или линии.

31.Момент количества движения системы материальных точек (кинетический момент)

Рассмотрим вектор количества движения материальной точки системы. Выберем в нашей инерциальной системе произвольный полюс А и определим момент вектора относительно этого полюса так же, как мы делали выше для сил:

(15)где — радиус-вектор, проведенный из полюса А к материальной точке.

Вектор называется моментом количества движения точки относительно полюса А. Главным моментом количества движения системы материальных точек относительно полюса А или кинетическим моментом системы относительно этого полюса называется вектор

Общности ради предположим теперь, что полюс А сам движется относительно той же самой инерциальной системы отсчета, по отношению к которой рассматривается движение системы материальных точек.

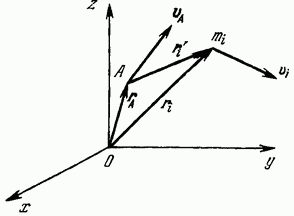Рис. III.2.Пусть — скорость полюса в некоторый момент. Обозначим далее через радиус-вектор из начала координат инерциальной системы отсчета к полюсу А, через — радиус-вектор из начала координат к точке системы, а через — радиус-вектор к этой же точке системы, отложенный из движущегося полюса А (рис. III.2); тогда

Дифференцируя это тождество, находим

По определению

Дифференцирование по t дает

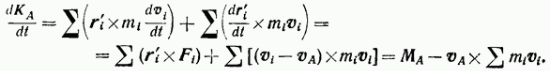
Но и ; используя эти равенства и меняя порядок сомножителей в векторном произведении, окончательно получаем

В частном случае, когда полюс А неподвижен относительно рассматриваемой инерциальной системы или совпадает с центром инерции С, векторное произведение в правой части выражения (17) равно нулю ипроизводная равна

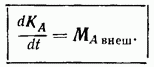Таким образом, мы доказали теорему об изменении кинетического момента:

Производная от кинетического момента системы материальных точек (относительно неподвижного полюса) равна главному моменту внешних сил, приложенных к точкам системы, относительно этого же полюса.

Для замкнутых систем выполняется условие так как на материальные точки замкнутой системы не действуют внешние силы. Поэтому при движении замкнутой системы материальных точек ее кинетический момент относительно любого неподвижного полюса не меняется. Это утверждение называется законом сохранения кинетического момента.

Если система не замкнута, но относительно какого-либо полюса , то из формулы (18) следует, что

(19)

Главный момент не зависит от выбора полюса только тогда, когда главный вектор . Поэтому у незамкнутых систем во время движения для любого полюса А, если одновременно выполнены два условия: для некоторого фиксированного полюса В и, кроме того, .

Разумеется, аналогичные утверждения верны и для проекций вектора на ось. Проектируя равенство (18) на произвольную неподвижную ось , получаем(20)

где — кинетический момент относительно оси , а — главный момент внешних сил относительно той же оси.

32. Закон сохранения импульса

Из теоремы об изменении количества движения системы следует, что в отсутствие внешних сил (замкнутая система), а также при равенстве суммы всех внешних сил нулю выполняется и. Иначе говоря, справедливо соотношение

Таким образом, следует вывод:

Если сумма всех внешних сил, действующих на систему, равна нулю, то количество движения (импульс) системы есть величина постоянная.

Данное утверждение составляет содержание закона сохранения количества движения системы^[2][3].

Возможны случаи, когда сумма внешних сил нулю не равна, но равна нулю её проекция на какое-либо направление. Тогда равно нулю и изменение проекции количества движения системы на это направление, т. е., как говорят, сохраняется количество движения в этом направлении.

33.Потенциальная энергия — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в полеконсервативных сил. Зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении^[1]. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы^[2]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

Единицей измерения энергии в Международной системе единиц (СИ) является джоуль.

Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.

Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными (потенциальными).

Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.

Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.

Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.

Потенциальная энергия тела в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

где —масса тела, —ускорение свободного падения, — высота положенияцентра масс тела над произвольно выбранным нулевым уровнем.