24.Теорема об изменении кинетической энергии

Кинетическая энергия механической системы — это сумма кинетических энергий всех ее материальных точек:

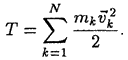
Вычислим дифференциал от выражения кинетической энергии и выполним некоторые простые преобразования:

Опуская промежуточные значения и применяя ранее введенный для обозначения элементарной работы символ , запишем:

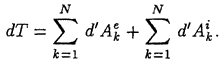
Итак, дифференциал кинетической энергии механической системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на точки системы. В этом и состоит содержание теоремы об изменении кинетической энергии.

Заметим, что сумма работ внутренних сил системы в общем случае не равна нулю. Она обращается в нуль только в некоторых частных случаях: когда системой служит абсолютно твердое тело; система абсолютно твердых тел, взаимодействующих при помощи не-деформируемых элементов (идеальных шарниров, абсолютно твердых стержней, нерастяжимых нитей и т.п.). По этой причине теорема об изменении кинетической энергии является единственной из общих теорем динамики, которая учитывает эффект действия внутренних сил.

Можно интересоваться изменением кинетической энергии не за бесконечно малый промежуток времени, как это делается выше, а за некоторый конечный промежуток времени . Тогда при помощи интегрирования можно получить:

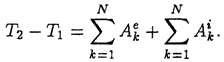
Здесь — значения кинетической энергии соответственно в моменты времени— суммы полных работ внешних и внутренних сил за рассматриваемый промежуток времени.

Полученное равенство выражает теорему об изменении кинетической энергии в конечной (интегральной) форме, которая может быть сформулирована так: изменение кинетической энергии при переходе механической системы из одного положения в другое равно сумме полных работ всех внешних и внутренних сил.

25.Уравнения равновесия плоской системы сил

 

Для равновесия произвольной плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы сумма проекций всех сил на каждую из двух прямоугольных осей, расположенных в плоскости действия сил, были равны нулю и сумма алгебраических моментов сил относительно любой точки, расположенной в плоскости действия сил, также была равна нулю:

 

                          (3.4)

 

Равенства (3.4) представляют так называемую основную форму условий равновесия при действии на тело плоской системы сил. Условия равновесия тела под действием плоской системы сил могут быть представлены еще в двух других формах.

Вторая форма условий равновесия:

 

                      (3.5)

 

т. е. должны быть равны нулю суммы моментов сил относительно любых двух точек А, В, расположенных в плоскости действия сил, и сумма проекций всех этих сил на ось х (при этом ось х не должна быть перпендикулярна прямой АВ).

Третья форма условий равновесия:

 

                   (3.6)

 

т. е. должны быть равны нулю суммы алгебраических моментов всех сил относительно любых трех точек А, В, С (эти точки расположены в плоскости действия сил и не лежат на одной прямой).

Если на объект действует плоская система параллельных сил, условия равновесия выражаются двумя формами уравнений равновесия:

                                  (3.7)

или

                            (3.8)

 

В формулах (3.7) ось у следует выбирать параллельно силам, центр А выбирается произвольно. В формулах (3.8) отрезок АВ не должен быть параллелен силам.

Направления осей координат х и у следует выбирать так, чтобы они были перпендикулярны неизвестным силам.

За центр моментов следует выбирать точку пересечения двух неизвестных сил или точку на линии действия неизвестной силы. 

Рациональный выбор формы уравнений равновесия, направления осей координат и центров моментов позволяет составлять такие уравнения равновесия, каждое из которых содержит по одной неизвестной.     Решение такой системы уравнений сопровождается минимумом вычислений.

 

26.ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ)

В некоторых задачах в качестве динамической характеристики движения точки вместо самого вектораколичества движения рассматривают его момент относительно некоторого центра или оси.

Эти моменты определяются так же, как и моменты силы (см. § 8, 14 и 28).

Таким образом, моментом количества движения точки относительно некоторого центра О называется векторная величина то определяемая равенством

где — радиус-вектор движущейся точки, проведенный из центра О.

При этом вектор направлен перпендикулярно плоскости, проходящей через и центр (рис. 224; для сравнения на нем показан и вектор ).

Момент количества движения точки относительно какой-нибудь оси проходящей через центр О, будет равенпроекции вектора на эту ось:

где — угол между вектором и осью Oz.

Теорема моментов устанавливает, как изменяется со временем вектор . Чтобы доказать ее, продифференцируем по времени выражение (35). Получим

Но как векторное произведение двух параллельных векторов, , где при действии нескольких сил . Следовательно,

В результате мы доказали следующую теорему моментов относительно центра: производная по времени от момента количества движения точки, взятого относительно какого-нибудь неподвижного центра, равна моменту действующей на точку силы относительно того же центра.

Сравнивая уравнения (37) и (32), видим, что моменты векторов и F связаны такой же зависимостью, какой связаны сами векторы 

Если спроектировать обе части равенства (37) на какую-нибудь ось проходящую через центр О, то, учтя соотношение (36), получим

Это равенство выражает теорему моментов относительно оси.

Из уравнения (37) следует, что если то , т. е. если момент действующей силы относительно некоторого центра равен нулю, то момент количества движения точки относительно этого центра есть величина постоянная. Такой результат имеет место в практически важном случае движения под действием центральной силы (см. § 86).

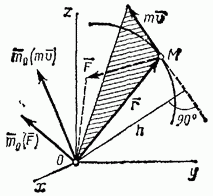Рис. 224

Рис. 225