Основное уравнение динамики

1.

F= ma

, или в векторной форме

2.	→ F = m → a

Единица СИ силы:

3.	[F]= нютон(Н)= кг · м с^2

Сила, определение

Силой в один ньютон называется такая сила, которая сообщает телу массой 1 (кг) ускорение 1 (м/с²).

44. Уравнениями Лагранжа второго рода называют дифференциальные уравнения движения механической системы, получаемые при применении лагранжева формализма.

Вид уравнений[править | править вики-текст]

Если голономная механическая система описывается лагранжианом (— обобщённые координаты, t — время, точкой обозначено дифференцированиепо времени) и в системе действуют только потенциальные силы, то уравнения Лагранжа второго рода имеют вид

где i = 1, 2, … n (n — число степеней свободы механической системы). Лагранжиан представляет собой разность кинетической и потенциальной энергий системы.

Если в системе действуют непотенциальные силы (например, силы трения), уравнения Лагранжа второго рода имеют вид

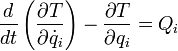
где — кинетическая энергия системы,  — обобщённая сила.

Вывод уравнений[править | править вики-текст]

Уравнения Лагранжа в механике получаются из законов динамики Эйлера (баланса количества движения и момента количества движения) при определенных ограничениях на систему (в ней должны присутствовать лишь идеальные голономные связи). Для других случаев получаются модификации уравнений Лагранжа. Отметим, что это частный (хотя и очень важный) случай механических систем.

Если для рассматриваемой системы применим принцип наименьшего действия, то вывод можно провести иначе. В лагранжевой механике вывод уравнений Лагранжа происходит на основе принципа наименьшего действия. Механическая система может быть описана некой функцией , называемой лагранжианом. Лагранжиан - это разность кинетической и потенциальной энергий системы. Принцип наименьшего действия гласит, что функционал

называемый действием принимает минимальное значение на траектории системы (здесь t₁ и t₂ — начальный и конечный моменты времени). Заметим, что необходимо доказать применимость принципа наименьшего действия к рассматриваемой системе: далеко не все физические системы ему подчиняются. Применяя к функционалу действию стандартную схему оптимизации, получаем для него уравнения Лагранжа — Эйлера, которые и называются уравнениями Лагранжа второго рода для механической системы.

Вывод уравнений для системы с одной обобщенной координатой и скоростью

Изменение действия при переходе из состояния в 

Разлагая эту разность по степеням

Варьируя это выражение, получаем:

Первое слагаемое заменяется по формуле Ньютона-Лейбница. Второе интегрируем по частям замечая что 

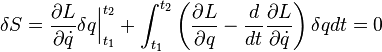
Первое слагаемое равно нулю исходя из самой первой формулы вывода. Второе слагаемое может быть равно нулю только если подынтегральное выражение равно нулю. Оно и является искомым уравнением Лагранжа: