28.Различные случаи определения положения мгновенного центра скоростей

Из предыдущего пункта видно, что вычисление скоростей при плоскопараллельном движении сильно упрощается, если положение мгновенного центра скоростей известно. Общий способ определения его положения рассмотрен выше. Ниже приводятся характерные частные случаи, когда положение мгновенного центра скоростей (сокращенно ) легко определяется.

1. Одна цилиндрическая поверхность катится без скольжения по другой цилиндрической поверхности (или плоскости), остающейся неподвижной. находится в точке соприкосновения плоских фигур подвижной и неподвижной поверхностей (рис. 104, а, б). Если при этом известна скорость какой-либо точки подвижного цилиндра, то это позволяет определить также направление вращения и величину угловой скорости (по формуле ).

2. Известны скорость одной точки тела (по величине и направлению) и направление скорости другой точки (штриховые линии на рис. 105).

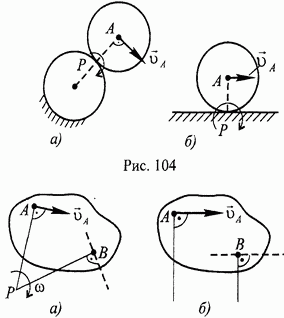
Рис. 105.

2.1. Направления скоростей не параллельны (рис. 105, а). Тогда находится в точке пересечения перпендикуляров, восставленных в этих точках к направлениям скоростей. Основанием к такому построению служит свойство 1) распределения скоростей в плоской фигуре (см. с. 110).

2.2. Направления скоростей параллельны (рис. 105, б). В этом случае указанные перпендикуляры не пересекаются, и не существует.

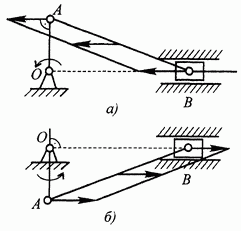
Рис. 106. Рис. 107.

Можно показать, что в этом случае угловая скорость тела равна нулю, а скорости всех его точек геометрически равны. Мы имеем так называемый случай мгновенного поступательного движения. В состоянии мгновенного поступательного движения, например, оказывается шатун АВ кривошипно-ползунного механизма каждый раз, когда кривошип ОА перпендикулярен направляющей ползуна В (рис. 106, а, б).

3. Известны скорости концов некоторого отрезка АВ плоской фигуры; направления скоростей перпендикулярны к этому отрезку. находится построением, показанным на рис. 107, а, б, вытекающим из свойства 2) распределения скоростей плоской фигуры (см. с. 110).

29.Теорема о движении центра масс Пусть все силы системы поделены на внешние и внутренние. Тогда дифференциальные уравнения движения системы запишутся в виде

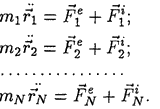
Почленно сложим левые и правые части уравнений:

По свойству внутренних сил последнее слагаемое в этом равенстве равно нулю. Левая часть равенства равна произведению массы системы на ускорение ее центра масс, т. е.

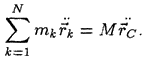
В этом легко убедиться, дифференцируя дважды по времени выражение для радиуса-вектора центра масс

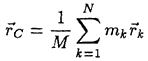
и разрешая результат относительно суммы 

В итоге равенство принимает вид

или, в проекциях на неподвижные координатные оси:

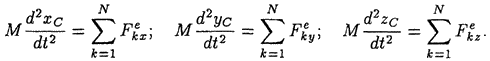
Получены дифференциальные уравнения, определяющие движение центра масс механической системы. Они выражают следующее правило, получившее название теоремы о движении центра масс механической системы:центр масс механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к точкам системы.