
- •6Способы определения координат центра тяжести
- •7Момент относительно точки
- •8Ускорение любой точки тела при плоском движении равно геометрической сумме ускорения полюса и ускорения во вращении точки относительно полюса.
- •9Пара сил, момент пары. Свойства пар сил.
- •11Мгновенный центр скоростей (мцс). Способы нахождения.
- •12Условия равновесия системы сходящихся сил
- •13Равновесие при наличии трения скольжения
- •14Основная теорема статики
- •15Поступательное движение твердого тела
- •23. Закон сохранения механической энергии
- •24.Теорема об изменении кинетической энергии
- •25.Уравнения равновесия плоской системы сил
- •27.Связи и их реакции
- •Основные типы связей и их реакции
- •6. Подвижная шарнирная опора. Реакция направлена перпендикулярно плоскости опоры (плоскости катания) (рис. 14, а, б).
- •28.Различные случаи определения положения мгновенного центра скоростей
- •29.Теорема о движении центра масс Пусть все силы системы поделены на внешние и внутренние. Тогда дифференциальные уравнения движения системы запишутся в виде
- •30.Координаты центров тяжести однородных тел
- •31.Момент количества движения системы материальных точек (кинетический момент)
- •34.Вынужденные колебания. Резонанс
- •37Глава 3. Параллельные силы и пары сил
- •Теорема Гюйгенса — Штейнера[править | править вики-текст]
- •Осевые моменты инерции некоторых тел[править | править вики-текст]
- •Основное уравнение динамики
- •Сила, определение
- •Вид уравнений[править | править вики-текст]
- •Вывод уравнений[править | править вики-текст]
37Глава 3. Параллельные силы и пары сил
3.1.
Сложение и разложение параллельных сил
Пусть
на тело действуют две параллельные
направленные в одну сторону
силы ![]() приложенные
в точках А и В.
приложенные
в точках А и В.
Согласно
1-й и 2-й аксиомам статики перейдем
отданной системы параллельных сил к
эквивалентной системе сходящихся сил ![]() .
(рис.
22
.
(рис.
22 ![]() )
)
Для
этого приложим в точка А и В две
уравновешивающие силы ![]() направленные
вдоль прямой АВ и сложим их с силами
направленные
вдоль прямой АВ и сложим их с силами![]() по
правилу параллелограмма. Полученные
силы
по
правилу параллелограмма. Полученные
силы![]() перенесем
в точку О, где пересекаются их линии
действия и разложим на первоначальные
составляющие. Силы
перенесем
в точку О, где пересекаются их линии
действия и разложим на первоначальные
составляющие. Силы![]() отбросим
(по 2-й аксиоме статики) и останутся две
направленные по одной прямой силы
отбросим
(по 2-й аксиоме статики) и останутся две
направленные по одной прямой силы![]() .
Эти силы переносим в точку С и заменяем
равнодействующей
.
Эти силы переносим в точку С и заменяем
равнодействующей![]() модуль
которой равен:
модуль
которой равен:
![]()
Для
определения положения точки С рассмотрим
треугольники ОаК, ОАС, ОСВ, Оbm. Из подобия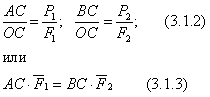
т.к. ![]() .
Далее учитывая свойства пропорций,
уравнение (3.1.1) и то, что
.
Далее учитывая свойства пропорций,
уравнение (3.1.1) и то, что
BC+AC=ABполучаем![]()
Рассмотрим случай сложения параллельных сдал направленных в разные стороны.
Пусть ![]() .
(рис.
23
.
(рис.
23 ![]() )
)
Выберем
на продолжении прямой АВ точку С и
приложим к ней уравновешенные
силы ![]() которые
параллельны
которые
параллельны![]() .
Положение точки С и модули сил выберем
таким образом, чтобы удовлетворялись
соотношения
.
Положение точки С и модули сил выберем
таким образом, чтобы удовлетворялись
соотношения

Складываем
силы ![]() и
и![]() ,
согласно (3.1.1) и (3.1.4), получим их
равнодействующую
,
согласно (3.1.1) и (3.1.4), получим их
равнодействующую![]() равную
по модулю
равную
по модулю![]() ,
то есть модулю
,
то есть модулю![]() и
приложенную в точке А. То есть
силы
и
приложенную в точке А. То есть
силы![]() и
и![]() оказались
уравновешенными и их можно отбросить.
оказались
уравновешенными и их можно отбросить.
В
итоге силы ![]() заменяются
одной силой
заменяются
одной силой![]() ,
которая и является их равнодействующей.
Точка приложения С равнодействующей и
ее модуль определяются формулами
(3.1.5), (3.1.6).
,
которая и является их равнодействующей.
Точка приложения С равнодействующей и
ее модуль определяются формулами
(3.1.5), (3.1.6).
С помощью формул (3.1.1.) - (3.1.6) можно решать задачу о разложении силы на две ей параллельные. Задача будет определенной при задании дополнительных условий.
3.2.
Пара сил. Момент пары
Система
двух равных по модулю, параллельных и
противоположно направленных
сил ![]() и
и![]() называется
парой сил.Система не находится в
равновесии, но и не имеет
равнодействующей.Плоскость, проходящая
через линии действия сил называют
плоскостью действия пары (рис.
24
называется
парой сил.Система не находится в
равновесии, но и не имеет
равнодействующей.Плоскость, проходящая
через линии действия сил называют
плоскостью действия пары (рис.
24 ![]() ).Расстояние
d между линиями действия сил пары называют
плечом пары.Действие пары сил на твердое
тело сводится к вращательному эффекту
и зависит от:
).Расстояние
d между линиями действия сил пары называют
плечом пары.Действие пары сил на твердое
тело сводится к вращательному эффекту
и зависит от:
1) модуля F и длины плеча d;
2) положения плоскости пары;
3) направления поворота в этой плоскости.
Для характеристики этого вращательного эффекта вводится понятие момент пары.
Моментом пары называется величина, равная взятому с соответствующим знаком произведению модуля одной из сил пары на ее плечо.
![]()
Момент пары условимся считать положительным (+), если пара стремится повернуть тело против хода часовой стрелки, и отрицательным (-) - когда по ходу часовой стрелки.
Обозначение
момента пары m или М без индекса имеет
свой смысл, так как момент пары нельзя
смешивать с моментом силы относительно
центра и этот центр указывается в индексе
(например: ![]() ).
Момент же пары определяется только
силами и плечом.
).
Момент же пары определяется только
силами и плечом.
Действие пары сил, как уже указывалось выше, характеризуется тремя условиями. При характеристике пар необходимо задавать все три значения. Но мы знаем, что вектор-нормаль к плоскости задает значения второго и третьего условия. Если мы теперь пронормируем вектор-нормаль значением момента пары, то все три условия будут выполнены. Эти соображения и позволили рассматривать момент пары как вектор.
Будем
изображать момент пары вектором ![]() или
или![]() ,
модуль которого равен модулю момента
пары, и который направлен перпендикулярно
плоскости действия пары, в ту сторону
откуда поворот пары виден происходящим
против хода часовой стрелки (рис.
25
,
модуль которого равен модулю момента
пары, и который направлен перпендикулярно
плоскости действия пары, в ту сторону
откуда поворот пары виден происходящим
против хода часовой стрелки (рис.
25 ![]() ).
).
Если рассматривать только пары лежащие в одной плоскости, то вместо вектора момента пары, можно стрелкой указывать только направлением поворота.
Вектор ![]() на
рис. 25 условно изображен выходящим из
точек В и D, однако он может изображаться
выходящим из середины АВ или CD или из
произвольной точки плоскости действия
пары, так как
на
рис. 25 условно изображен выходящим из
точек В и D, однако он может изображаться
выходящим из середины АВ или CD или из
произвольной точки плоскости действия
пары, так как
![]()
3.3.
Сложение пар. Условия равновесия пар
Рассмотрим первоначально систему пар лежащих в одной плоскости.
Теорема: Система пар, лежащих в одной плоскости, эквивалентна одной паре, лежащей в той же плоскости и имеющей момент, равный алгебраической сумме моментов слагаемых пар.
Пусть
на тело действуют три пары сил с
моментами ![]() (рис.
26
(рис.
26 ![]() )
)
Используя
теорему об эквивалентности пар, заменяем
эти пары эквивалентными другими парами ![]() ,
имеющими общее плечо d и такие же моменты
,
имеющими общее плечо d и такие же моменты
![]()
Сложив отдельно силы получим:
![]()
Вся
система заменится одной парой ![]() с
моментом
с
моментом
![]()
Обобщая эту формулу на n-пар получим:
![]()
Для равновесия плоской системы пар необходимо и достаточно, чтобы алгебраическая сумма моментов этих пар была равна нулю:
![]()
При сложении пар в пространстве достаточно будет рассмотреть две пары.
Теорема: Любая система пар, действующая на твердое тело, эквивалентна одной паре с моментом, равным геометрической сумме моментов слагаемых пар.
![]()
Итак,
пусть даны две пары с моментами m1 и m2,
лежащие в плоскостях I и II (рис.
27 ![]() )
)
Складываем силы в точках А и В:
![]()
и
убеждаемся, что пары ![]() заменяются
одной парой
заменяются
одной парой![]() .
Найдем момент
.
Найдем момент![]() этой
пары
этой
пары

Если
на тело действует л пар с моментами ![]() ,
то:
,
то:
![]()
Геометрически
вектор ![]() -
это замыкающий вектор силового
многоугольника.
-
это замыкающий вектор силового
многоугольника.
Если
векторы ![]() лежат
в разных плоскостях, то можно ввести
систему координат Oxyz и находить
лежат
в разных плоскостях, то можно ввести
систему координат Oxyz и находить![]() аналитически:
аналитически:
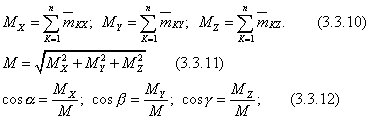
Условия равновесия твердого тела под действием пространственной системы пар, запишутся:
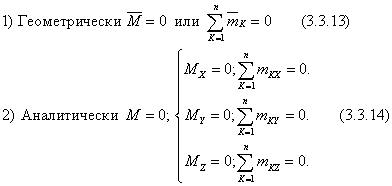
38. Из второго закона динамики материальной точки
![]() ,
(1.1)получается следующие дифференциальные
уравнения:
,
(1.1)получается следующие дифференциальные
уравнения:
- дифференциальные уравнения движения точки на плоскости
![]() ,
,
![]() ,
(1.2)- дифференциальное уравнение движения
точки по прямой
,
(1.2)- дифференциальное уравнение движения
точки по прямой
![]() ,
(1.3)
,
(1.3)
где ![]() ,
,![]() -
проекции ускорения
-
проекции ускорения![]() на
оси декартовых координат.
на
оси декартовых координат.
Первой называется задача, в которой заданы масса точки и закон ее движения в декартовых или естественных осях. Необходимо определить модуль и направление силы, действующей на точку.
Для решения следует выполнить следующие операции:
- построить расчетную схему, на которой в соответствии с условием задачи изобразить систему осей координат, нарисовать траекторию точки и отметить на траектории то положение точки, для которого требуется найти действующую силу. Эту силу следует представить составляющими на выбранные ос координат;
- по заданному движению материальной точки определить проекции ее ускорения на принятые оси координат;
- составить дифференциальные уравнения движения точки в форме (1.2) или (1.3). Из полученных уравнений определить проекции искомой силы, а затем ее модуль и направляющие косинусы.
Рассмотрим пример выполнения теста 1.
«Материальная
точка М массой ![]() кг
движется в горизонтальной плоскости
согласно уравнениям
кг
движется в горизонтальной плоскости
согласно уравнениям![]() ,
,![]() ,
где
,
где![]() -
в метрах,
-
в метрах,![]() -
в секундах. Определить силу
-
в секундах. Определить силу![]() ,
действующую на точку в момент
,
действующую на точку в момент![]() с.».
с.».
Решение
Строится
расчетная схема. В соответствии с
условием задачи принимается декартовая
система координат. Из заданных уравнений
движения следует, что траекторией точки
является парабола ![]() .
Она изображена на рисунке 1.1.
.
Она изображена на рисунке 1.1.
Положение
точки в момент ![]() с.
определяется координатами:
с.
определяется координатами:
![]() м;
м; ![]() м.
м.
М1 (0,5; -0,5).
Искомую
силу представим составляющими ![]() и
и![]() .
.
Вычислим проекции ускорения точки на оси координат
![]() ,
, ![]() .
.
Для
заданного момента ![]() с.
имеем
с.
имеем
![]() м/с2,
м/с2, ![]() м/с2.
м/с2.
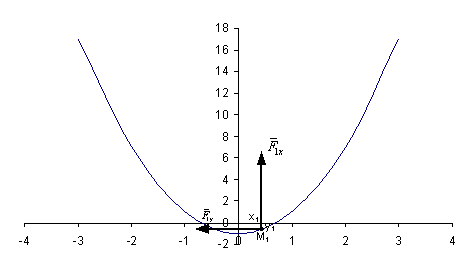 Рисунок
1.1 – траектория точки
Рисунок
1.1 – траектория точки
Из дифференциальных уравнений (1.2) находим
![]() Н,
Н, ![]() Н.
Н.
Затем определяем модуль силы
![]() Н.
Н.
и направляющие ее косинусы
![]() ,
, ![]() .
.
39. Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величинаJa, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
![]() ,где:
,где:
mi — масса i-й точки,
ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, какмасса тела является мерой его инертности в поступательном движении.
![]() ,
,
где:
dm = ρ dV — масса малого элемента объёма тела dV,
ρ — плотность,
r — расстояние от элемента dV до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
![]()
