Свойства непрерывных функций

1. Сумма и произведение непрерывных функций есть непрерывная функция.

2. Частное непрерывных функций есть непрерывная функция для всех точек в которых знаменатель отличен от нуля.

3. Функция непрерывная на отрезке: а ) ограничена; б) достигает на этом отрезке своих неибольшего и наименьшего значений; в) принимает на отрезке любое из промежуточных между своими наимельшим и наибольшем значение.

4. Если и- непрерывны функции, то их композиция - сложная (стоставнаяяя0 функция- также непрерывна на соответствующем отрезке.

Последнее свойство может быть объяснено (и доказано) с помощью определения непреывности в точке, переписанного в следующей форме:

Из перечисленных свойств следует, что непрерывнымси являются функции

, ,,и подобные.

Производные фоункции

Пусть переменная х например, (аргумент функции), имевшая некое начальное значение х₀, приняла значения х. Разность х – х₀ назовем приращением переменной (аргумента) ч в точке х₀ обозначив его ∆ х. Итак, по определению

∆ х = х – х₀.

Если функция у = f (х) определена как при х = х₀, так и при х = х₀ + ∆ х, то разность f (х₀ + ∆ х) - f (х) ≡ ∆ у называют приращение функции у = f (х) в точке х = х₀, которое отвечает приращению аргумента на ∆ х. Заметим, что как ∆ х, так и ∆ у могут быть как положительными, так и отрицательными величинами. Нетрудно увидеть, что если у = f (х) непрерывна в точке х₀, то при ∆ х → 0 соответствующее ∆ у также стремится к нулю. Поэтому уверждение это принимается как второе определение непрерывности. Можно предположить, что величины ∆ у = f (х₀ + ∆ х) – f (х) взятые для разных непрерывных в точке х₀ функций и по “разному” вслед за ∆ х (“быстрее” или “медленее”), стремясь к нулю, несут в себе некую информацию о поведении функци в точке х₀. Для выявления этой информации рассмотрим переменную величину и вычмслим ее предел при ∆ х → 0, обозвав этот предел производной функции. Итак

Производной от функций у = f (х) в точке х₀ называют предел к которому стремится приращение функции к приращению аргумента, когда последний стремится к нулю.

О

бозначив проиводную одним из общепринятых символов у'(х);f' (х); ;, по определению имеем:

Отметим три самых важных “смысла” производной функций, имеющих некую физическую или геометрическую “суть”.

1. Пусть замкнутый интервал [a¸x] обозначает кусок метериального неоднородного по массе, достаточно (чтобы пренебречь толщиной) тонкого стержны - “отрезка [a¸b] (рис. 3), а m (х) - масса этого куска (очевидно, m (а) = 0). Тогда величина

согласно известному физическому определению выражает плотность массы этого неоднородного стержны в точке.

2. Пусть t – время, а S (t) - зависимостьпути прямолинейного движения от времени (S (0=). Тогда физически очевидно, что

выражает мгновенную скорость этого прямолинейного движения в данный момент времени.

3. Рассмотрим график (γ) функции у = f (х) и определим касательную к этому графику (и вообще кривой) как предельное положение секущей (М₀, М), кодга М “бежит” к М₀ по (γ), если такое “положение” существует и не зависит от “стороны” на (γ) по которой М бежит М₀ (см. рис.).

Тогда, считая М имеет абсциссу х₀ + ∆ х, и устремляя ∆ х к 0 (следи за рис. 4) имеем:

; .

Итак, из определения следует, что величина это угловой коэффициент касательной (р) к графику (γ) в точке М₀. Отсюда уравнение этой касательной можно записать так:

Пример. Написать уравнения касательных к графику функции у = х²

а) в точке с абсциссой х = 3; б) в произвольной ее точке х₀.

Итак, f (3) = 3², f (3+∆х)=(3+∆х)². Тогда по определению

Таким обоазом, к = 6 и уравнение искомой касательной - у – 9 = 6 (х-3).

б) по определению

Таким образом, уравнение касательной к графику у = х² в общем виде

у – х₀² = 2 х₀ · (х – х₀).

По ходу решений примера сы выяснили, что производная функции х² в любой фиксированной точке х (“без нолика”) равна 2х. Точно также можно показать, что (х³)' = 3 х² и т.д.

Это наводит на мысль о том, что производная любой функций - это некая вполне определенная для нее функция. Поэтому, чтобы для вычисления производных - “по научному - дифференцирования” - не прибегать каждый раз к определению - вычислению “скучных” пределов вполне естественно составить список - таблицу производных самых распространённых - элементарных функций. Для примера:

1.

.

2.

Перед тем как продолжить составление таблицы, приведем несколько общих правил дифференцирования. Прежде всего из свойств пределов легко следует, что если - дифференцируемые функции, а С - константа, то

1. ;

2. ;

3. ;

4. ;

5. .

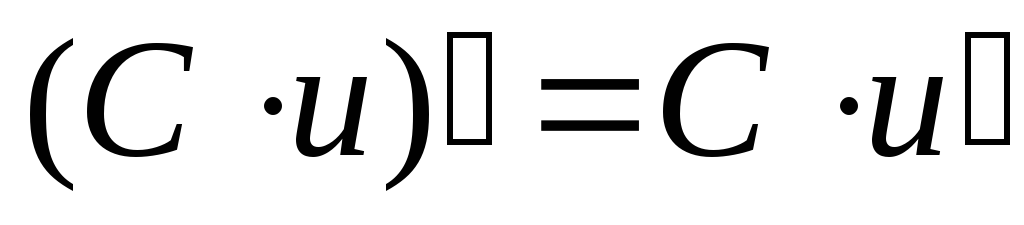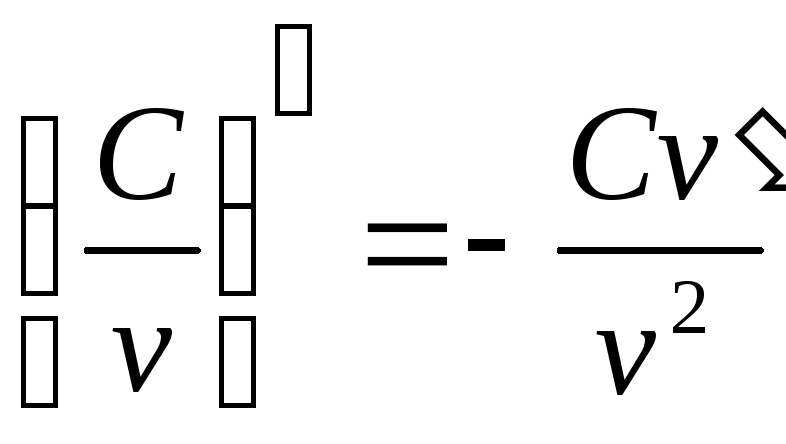Это, так сказать, «арифметические» правила дифференцирования. Однако правилом наиважнейшим, позволяющим превратить дифференцирование в алгебраическое действие - «исчисление», а некотором смысле схожее, например, с операцией умножения десятичных чисел «столбиком» является