Дифференциал функции.

Переобзовем приращение независимой переменной х дифференциалом этой переменной, обозначив его как dx, то есть для независимой переменной по определению будем считать

Теперь

Назовём дифференциалом функции у=f(х) выражение

Обозначив его символом dy или df (х) по определению будем иметь

Последняя формула называется «формой» «первого» дифференциала. Забегая вперед приведём и объясним «архиважнейшее» свойство дифференциала - так называемую инвариантность (неизменность) его формы. Итак

Форма дифференциалане зависит(инвариантна) от того, является лихнезависимой переменной, или же этах- зависимая переменная - функция.

Действительно, пусть , то есть у - сложная функция «от t» По определению дифференциала имеем. Но

.

Поэтому

,

то есть опять имеет ту же форму.

Однако «суть» (а не форма) дифференциала в этих двух случаях разная. Чтобы это объяснить выясним сначала геометрический смысл дифференциала и некоторые другие его свойства. Из приведенного ниже рисунка видно, что дифференциал является частью приращения ∆у. Можно показать, что dy, есть главная и линейная часть ∆у. Главная в том смысле, что разность ∆у – dy есть величина бесконечно малая высшего, что ∆х порядка малости, а линейная в смысле линейности своей зависимости от ∆х.

Можно сказать также, что дифференциал есть (смотри рисунок) соответствующее приращение ординаты касательной. Теперь объяснима и разница в сути и значении дифференциальной формы при независимом и зависимом аргументе. В первом случае dx есть все приращение ∆х. С помощью определения легко доказываются и

Арифметические свойства дифференциала

1. ; 2. ; 3..

Определим теперь

Производные и дифференциалы высших порядков.

По определению - вторая производная;- третья производная и вообще- n – ая производна функции.

Примеры

1.

2.

;

; ...

Точно также по определению

; - второй дифференциал; - третий дифференциал и вообще - n – ый дифференциал функции. Можно

показать, что

Примеры:

1. ,

2. .

Приложения производных к исследованию функций.

В

ажнейшей теоремой, на которой базируется почти все методы исследования функций, являетсятеорема Лангранжа: Если функция f (ч) непрерывна на отрезке (а, b) и дифференцируема во всех внутренних его точках, то найдется такая точка, что

Геометрически (рис. 6) теорема утверждает, что на соответствующем интервала найдется точкатакая, что угловой коэффициент касательной к графику в точкеравен угловому коэффициенту секущей, проходящей через точкии.

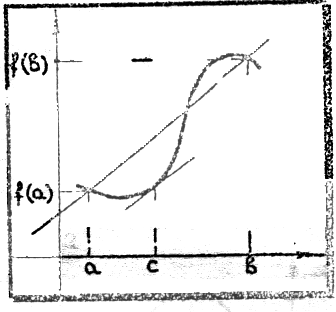
Другими словами, для «куска» графика описанной в теореме функции, найдется касательная, параллельная секущей, которая проходит через граничные точки этого куска. Из этой теоремы в частности следует замечательное правило раскрытия неопределенностей типа -так называемой правило маркиза Лопиталя [L'Hôpital]: Если функции f(x) и g(x) дифференцируемы в точке а и некоторой её окрестности f(а) = g(а) = 0, а f'(а) и g'(а) не равны нулю одновременно то .

Замечания: Можно показать, что 1. Правило применимо и для раскрытия неопределенности типа ; 2. Еслиf'(а) = g'(а) = 0 или ∞, а f''(а) и g''(а) существует и не равны нулю одновременно, то .

Пример:

Спомощью теоремы Лангранжа можно доказать и достачныц признак монотонности функции:

Если на интервале (а, b) тоf(x) возрастает (убывает) на этом интервале.

Следует отметить, что знако постоянство производной является и необходимым признаком монотонности. А уже из этих признаков можно вывести:

а) необходимый признак существования экстремума

Для того чтобы точка х₀ была точкой максимума (минимума), необходимо, чтобы f'(x₀) либо была равна нулю, либо не существовала. Такие точки х₀, в которых f'(x₀) = 0 или не существуют называют критическими.

б) достаточный признак существования экстремума:

Если (см. рис.) при переходе через критическую точку х₀ производная f'(x) функции меняет знак, то эта точка - точка экстремума. Если, при этом, f'(x) меняет знак с «+» на «- « , то х₀ - точка максимума, а если с «-« на «+», то точка х₀ - точка минимума.

И наконец, приведем еще один признак, использующий понятие производной. Это

Достаточный признак выпуклости (вогнутости) графику функции «над» интервалом (а, b).

Если на интервале (а, b) производная f''(x)>0 то график f(x) вогнут, а если f''(x)< 0, то график является выпуклым «над» этим интервалом.

Полная схема исследования функции может теперь выглядеть следующим образом:

Схема полного исследования функции

1. Область определения интервала знакопостоянства.

2. Асимптоты.

3. Четность, периодичность.

4. Интервалы монотонности, экстремумы.

5. Выпуклость, вогнутость.

6. График функции (с выше найденными контрольными точками).

2. Пример: Исследовать и построить график функции

.

1. .

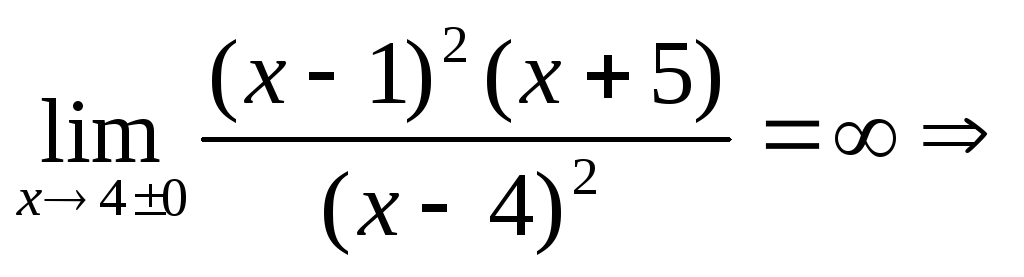2. а) х = 4 - вертикальная асимптота;

б) ,

в) у = х + 8 - наклонная асимптота,

3. = - значит данная функция «общего вида».

4. 

Приравнивая производную к нулю и выяснив её знаки на образовавшихся интервалах постоянства, получаем таблицу:

х	-∞, - 2	-2	-2, 1	1	1, 4	4	4, 13	13	13, ∞
у'	+	0	-	0	+	не сущ.	-	0	+
у	возр.	0,75	убыв.	0	возр.	не сущ.	убыв.	32	возр.
						асс.

5. - точка перегиба.

6. График функции изображен на рисунке.