
- •Волжская государственная академия водного транспорта
- •Основные понятия из линейной алгебры и дифференциального исчисления.
- •В. Даль «Толковый словарь…» матричная азбука Основные определения и обозначения
- •Действия с матрицами
- •Определители матриц.
- •Таким образом, по определению для любого натурального n имеем
- •Свойства определителей
- •Обратная матрица
- •Ранг матрицы.
- •Решение систем
- •I. Метод обратной матрицы.
- •II. Правило Крамера.
- •III. Метод Гаусса
- •Векторная азбука Основные определение и обозначения
- •Линейные действия с векторами.
- •Базис и координаты.
- •Система координат «точечного» пространства.
- •Задача о делении отрезка в данном отношении.
- •Правило вычисления векторного произведения
- •Основные приложения векторного произведения
- •Смешанное произведение векторов.
- •Азы аналитической геометрии. Уравнения прямой на плоскости.
- •Угол между прямыми.
- •Расстояние от точки до прямой.
- •Уравнения плоскости в пространстве.
- •Расстояние от точки до плоскости.
- •Уравнение прямой в пространстве.
- •Параметрические уравнения прямой –
- •Канонические уравнения прямой
- •Расстояние от точки до прямой
- •Замечания о взаимном расположении.
- •Кривые второго порядка.
- •Азбука дифференциального исчисления. Переменные величины.
- •Предел переменной
- •«Монотонная и ограниченная последовательность имеет предел»
- •Характеристический признак существования предела.
- •Сравнение бесконечно малых переменных величин.
- •Характеристическое свойство бесконечно малых
- •Непрерывность.
- •Асимптоты функции
- •Свойства непрерывных функций
- •Производные фоункции
- •Правило дифференцирования сложной функции
- •Дифференциал функции.
- •Арифметические свойства дифференциала
- •Производные и дифференциалы высших порядков.
- •Приложения производных к исследованию функций.
- •Азы дифференциального исчисления функции нескольких переменных. Основные определения
- •Производные функции многих переменных.
- •Дифференцирование неявных функций
- •Дифференциал функции двух переменных. Касательная плоскость и нормаль к поверхности.
- •Старшие производные
- •Экстремумы функций двух переменных.
- •Векторная функция скалярного аргумента
- •Задания к контрольной работе № 1
- •Задания на контрольную работу № 2
- •Литература
Векторная функция скалярного аргумента
Назвем
вектор - функцией скалярного аргумента
правило по которому каждому значению
числовой (скалярной) переменной t
ставится в соответствие единственный
и четко определенный радиус вектор
![]() (см. рис.), записывая э
(см. рис.), записывая э то
так:
то
так:![]()
Ясно,
что для того, чтобы задать вектор
![]() ,
достаточно задать три «скалярные»
функции - координаты:
,
достаточно задать три «скалярные»
функции - координаты:![]() ,
то есть
,
то есть
![]() =
(
=
(![]() ).
).
Естественно
вектор
![]() называют приращением вектор - функции
называют приращением вектор - функции![]() .
Вектор
.
Вектор
![]()
Называют производной вектор – функции скалярного аргумента.
Из свойств пределов и операций с координатами вектора следует, что
![]() =
(
=
(![]() ).
).
К ривая
(траектория), которую описывает конец
М радиус - вектор
ривая
(траектория), которую описывает конец
М радиус - вектор![]() ,
называется годографом вектор -
функции. Тогда, если трактовать t как
время (а годограф - как траекторию
движения), то вектор
,
называется годографом вектор -
функции. Тогда, если трактовать t как
время (а годограф - как траекторию
движения), то вектор![]() ,
очевидно, выражает вектор скорости
движения «материализовавшейся» точки
М вдоль соответствующего годографа.
,
очевидно, выражает вектор скорости
движения «материализовавшейся» точки
М вдоль соответствующего годографа.
Геометрически,
и это следует из определения вектор
![]() направлен по касательной к годографу,
почему каноническое уравнение
касательной прямой к годографу
(«пространственной» кривой) с
произвольной точкой касания можно
записать в виде.
направлен по касательной к годографу,
почему каноническое уравнение
касательной прямой к годографу
(«пространственной» кривой) с
произвольной точкой касания можно
записать в виде.
![]() .
.
Рассмотрим
«плоскую» вектор - функцию
![]() = (
= (![]() ).
).
Тогда
уравнения

которое
определяют своеобразную зависимость
«у от х» через «общий» аргумент t
называют параметрическими уравнениями
плоской кривой или уравнениями функции
«у от х» «заданной параметрически».
Естественно, и в этом случае можно
говорить о производной «от у по х»,
то есть о
![]() .
Можно показать, что она также является
функцией заданной параметрически и
определяется уравнениями
.
Можно показать, что она также является
функцией заданной параметрически и
определяется уравнениями

. (*)
Последнее уравнение здесь (в правой части - выражение «от t») и определяет параметрическую зависимость «у' от х». Эти же последние уравнения определяют и «методику» нахождения «старших» производных (второй, третьей и т.д.) от функции заданной параметрически. Нужно рассматривать каждую «предыдущую» производную, как «новую», параметрически заданную функцию, и записывать для нее соответствующие уравнения (*) как для «первой» производной.
Пример:
 ;
;
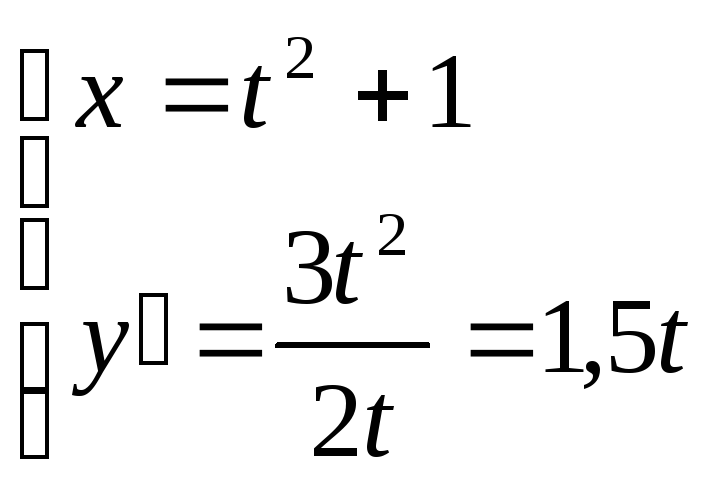 ;
; ;
; ;
.....
;
.....
Задания к контрольной работе № 1
1. Решить систему тремя способами: а) с помощью обратной матрицы, б) по правило Крамера, в) с помощью процедуры Гаусса.
1)
 2)
2)
3)
 4)
4)
5)
 6)
6)
7)
 8)
8)
9)
 10)
10)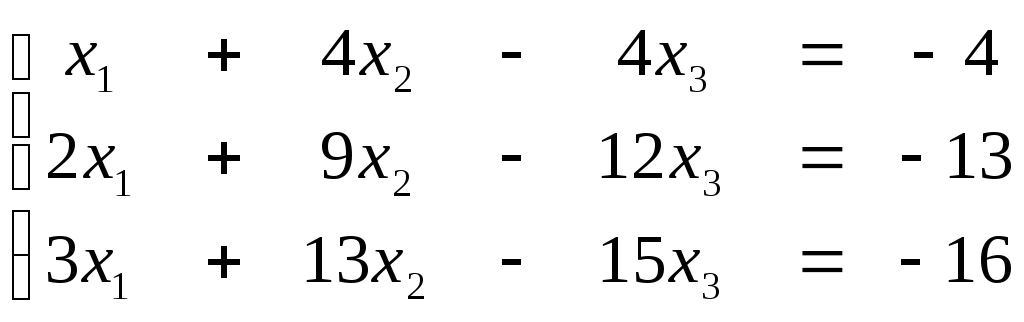
11)
 12)
12)
13)
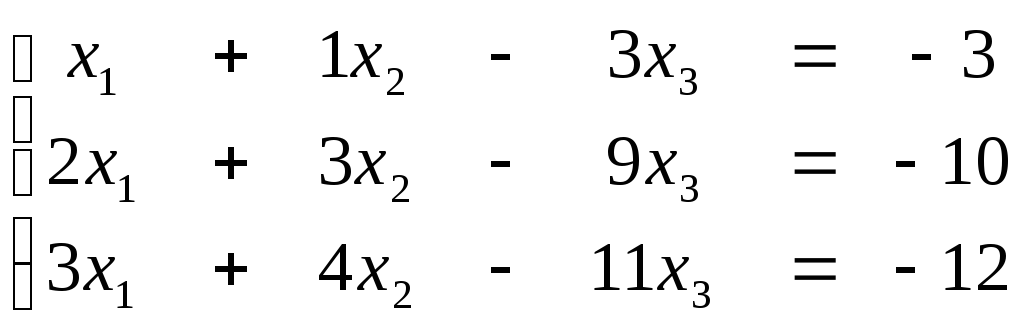 14)
14)
15)
 16)
16)
17)
 18)
18)
19)
 20)
20)
21)
 22)
22)
23)
 24)
24)
25)
 26)
26)
27)

3.
Для пирамиды А,В,С,D, координаты вершин
которой заданы в таблице 2, найти:
координаты и длины векторов ребер
![]() ,
,![]() ,
,![]() угол ВАС, площадь гран (ВАС) и объём
пирамиды; уравнения ребра (АD), грани
(ВАС), а также высоту и длину высоты
(DН).
угол ВАС, площадь гран (ВАС) и объём
пирамиды; уравнения ребра (АD), грани
(ВАС), а также высоту и длину высоты
(DН).
Таблица 2
|
N |
А |
В |
С |
D | ||||||||
|
ха |
уа |
zа |
хb |
уb |
zb |
хс |
ус |
zс |
хd |
уd |
zd | |
|
1 |
0 |
1 |
-1 |
6 |
-2 |
-3 |
4 |
5 |
-3 |
1 |
3,5 |
6 |
|
2 |
1 |
0 |
1 |
8 |
-2,5 |
0 |
4 |
4,5 |
0 |
2 |
4 |
9 |
|
3 |
1 |
-1 |
0 |
9 |
-5 |
-1 |
6 |
4,5 |
1 |
2 |
4 |
12,5 |
|
4 |
1 |
1 |
1 |
10 |
-4 |
0,5 |
4 |
3 |
1 |
3 |
2 |
7 |
|
5 |
-1 |
-1 |
-1 |
4 |
-1 |
-1 |
4 |
11,5 |
-2 |
1,5 |
-1 |
5 |
|
6 |
0 |
0 |
-1 |
7,5 |
-4 |
-1 |
2,5 |
6 |
-1 |
0,5 |
3 |
8 |
|
7 |
-1 |
0 |
0 |
5 |
-2,5 |
0 |
2 |
9 |
-0,5 |
-1 |
0 |
7 |
|
8 |
-1 |
0 |
-1 |
5 |
-3 |
-3 |
3 |
4 |
-3 |
0 |
2,5 |
6 |
|
9 |
0 |
-1 |
0 |
7 |
-3,5 |
-1 |
3 |
3,5 |
-1 |
1 |
3 |
8 |
|
10 |
0,5 |
0,5 |
0,5 |
8,5 |
-3,5 |
-0,5 |
5,5 |
6 |
-0,5 |
1,5 |
5,5 |
13 |
|
11 |
0,5 |
-0,5 |
0 |
9,5 |
-3,5 |
-0,5 |
3,5 |
3,5 |
0 |
2,5 |
2,5 |
6 |
|
12 |
0 |
0 |
0,5 |
5 |
0 |
0,5 |
5 |
12,5 |
-0,5 |
2,5 |
0 |
6,5 |
|
13 |
2 |
-1 |
-1 |
9,5 |
-5 |
-1 |
4,5 |
5 |
-1 |
2,5 |
2 |
8 |
|
14 |
1 |
-2 |
-1 |
7 |
-4,5 |
-1 |
4 |
7 |
-1,5 |
1 |
-2 |
6 |
|
15 |
0 |
-2 |
1 |
6 |
-5 |
-1 |
4 |
2 |
-1 |
1 |
0,5 |
8 |
|
16 |
0 |
0 |
-2 |
7 |
-2,5 |
-3 |
3 |
4,5 |
-3 |
1 |
4 |
6 |
|
17 |
0 |
-2 |
0 |
8 |
-6 |
-1 |
5 |
3,5 |
-1 |
1 |
3 |
12,5 |
|
18 |
1 |
0 |
1 |
10 |
-3 |
0,5 |
4 |
4 |
1 |
3 |
3 |
7 |
|
19 |
1 |
-1 |
0 |
6 |
-1 |
0 |
6 |
11,5 |
-1 |
3,5 |
-1 |
6 |
|
20 |
1 |
-1 |
1 |
8,5 |
-5 |
1 |
3,5 |
5 |
1 |
1,5 |
2 |
10 |
|
21 |
-1 |
-1 |
-1 |
5 |
-3,5 |
-1 |
2 |
8 |
-1,5 |
-1 |
-1 |
6 |
|
22 |
0 |
0 |
-1 |
6 |
-3 |
-3 |
4 |
4 |
-3 |
1 |
2,5 |
6 |
|
23 |
-1 |
0 |
0 |
6 |
-2,5 |
-1 |
2 |
4,5 |
-1 |
0 |
4 |
8 |
|
24 |
-1 |
0 |
-1 |
7 |
-4 |
-2 |
4 |
5,5 |
-2 |
0 |
5 |
11,5 |
|
25 |
0 |
-1 |
0 |
9 |
-4 |
-0,5 |
3 |
3 |
0 |
2 |
2 |
6 |
4. Построить кривые приведя их уравнения к каноническому виду
1)
 2)
2)

3)
 4)
4)

5)
 6)
6)

7)
 8)
8)

9)
 10)
10)

11)
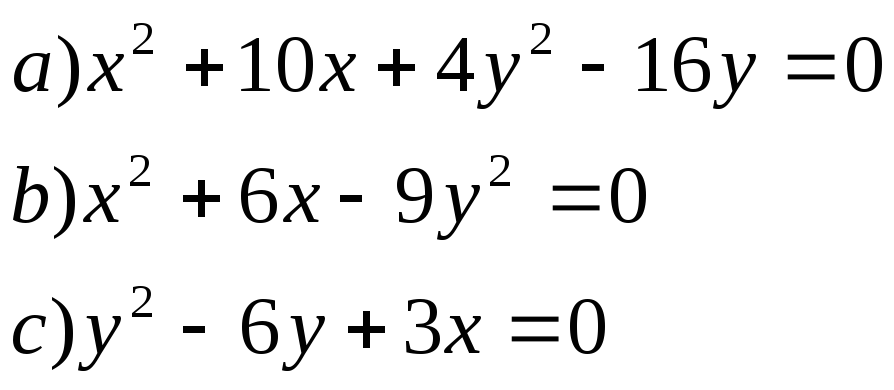 12)
12)
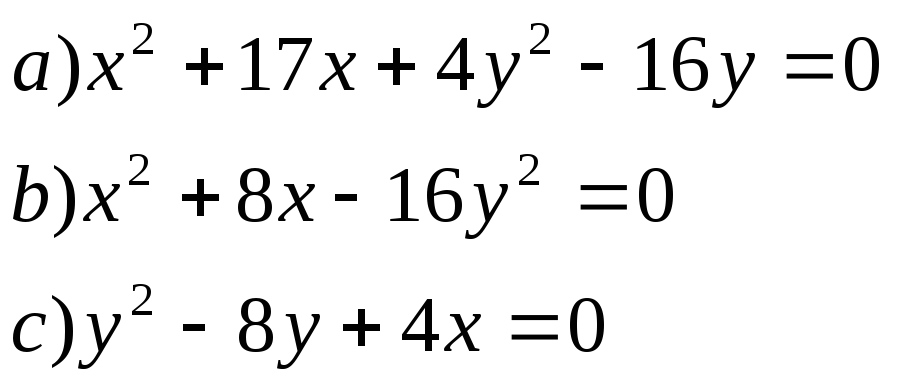
13)
 14)
14)

15)
 16)
16)

17)
 18)
18)

19)
 20)
20)

21)
 22)
22)

23)
 24)
24)

25)

