Определители матриц.

Понятие определить или (синоним) детерминант матрицы вводится для любой квадратной и только квадратной матрицы. Изображают определитель любой такой матрицы

А =

«сложным» символом

а обозначают чаще всего одним из символов ∆ (а), det (A), или просто ∆.

Договорились, что определителем квадратной матрицы называется величина, формируемая из её элементов с помощью следующих понятий и соглашений:

• Определителем матрицы первого порядка называют её единственный элемент;

• Минором (ЛЮБОЙ!!!) матрицы называют определитель всякой квадратной матрицы встроенной в данную. Другими словами минором к- го порядка некоторой матрицы состоящей из элементов данной матрицы, которые находились на пересечении любых её "k" строк и "k" столбцов.

• Дополнительным минором к элементу а_ij квадратной матрицы А называют минор – определитель М*_ij матрицы, полученной из данной вычеркиванием i – ой строки и j – го столбца.

• Алгебраическим дополнением к элементу а_ij квадратной матрицы А называют величину

А*_ij = (-1)^i+j · М*_ij

и

Определителем матрицы n – го (n≥2) порядка назовем сумму произведений элементов первой строки матрицы на их собственные алгебраически дополнения.

, наконец

Таким образом, по определению для любого натурального n имеем

Процесс вычисления определителя по такой формуле часто называют разложением определителя по (первой) строке.

Из вышеизложенного сразу следует что:

А. Для n = 2, то есть для матрицы

А = : М^*₁₁ = а ₂₂, М^*₁₂ = а ₂₁ А^*₁₁ = (-1)² · М^*₁₁ = а ₂₂,

А^*₁₂ = (-1)³ · М^*₁₂ = - а ₂₁, а значит det (А) = а₁₁ · А₁₁ + а₁₂ · А₁₂,

то есть

Б

= а₁₁ · а₂₂ – а₁₂ · а₂₁

. Для n = 3, то есть для матрицы

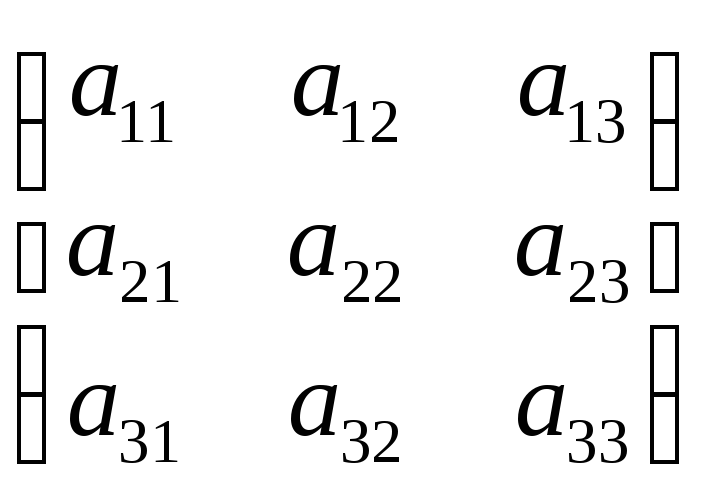А = : М^*₁₁ = , М^*₁₂ = ,

М^*₁₃ = , А^*₁₁ = М^*₁₁, А^*₁₂ = - М^*₁₂, А^*₁₃ = М^*₁₃, а значит = а₁₁ · - а₁₂ · + а₁₃ ·

Примеры: = 10 – (3) = 13;= - 50 – (-35) = -15;= 1 ·

- 3 · + (-5)·= (13+33) – 3 · (-26+30) – 5(-22-10) = 194.

Свойства определителей

1. Для любых 1 ≤ i ≤ n

Иначе говоря, определитель всякой матрицы может быть вычислен «разложением по любой строке.

Пример:

. Раскладывая этот определитель по первой, второй и третьей строке последовательно получаем:

.

2. 

Из этого свойства и свойства 1., в частности, следует, что определитель может быть вычислен для любого 1 ≤ j ≤ n по формуле

то есть «разложением» по любому столбцу.

Пример. Раскладывая определитель из первого примера по первому, второму и третьему столбцу последовательно получаем:

.

3. Если k – тый (1 ≤ k ≤ n) столбец (строка) матрицы представлен в виде суммы неких двух столбцов (строк), то её определитель может быть получен как сумма определителей матриц у которых k – тым столбцом является соответствующий столбец (строка) - слагаемое.

Пример: Все для того же определителя ∆ имеем

-2 = ∆ =

4. При умножении столбца (строки) матрицы на число λ её определитель умножается на то же самое число.

Пример:Умножив в «нашем» ∆ на вторую строку на 5 и раскладывая по этой строке «новый» определитель получаем

5. При перестановке двух любых строк (столбцов) матрицы её определитель меняет знак.

Пример. Переставив «в ∆» первую и третью строку получаем

6. Равен нулю определитель любой матрицы имеющей две одинаковые строки (столбца).

Пример: .

Из этого свойства, в частности, следует что равна нулю сумма произведений элементов любой строки (столбца) на алгебраические дополнения другой строки (столбца) то есть

7. Определитель матрицы не меняется, если к любой её строке (столбцу) прибавить произвольную комбинацию остальных строк

Пример: прибавив ко второй и третьей строкам определителя ∆ его же первую, получаем: