Homo institutius - Человек институциональный - Иншаков - 2005 - 854

Дискуссионные проблемы развития институциональной теор ии

Как видно, на последнем этапе адаптации происходит скач- кообразное (вдвое) уменьшение числа ребер с появлением но вого качества — «матричности» структуры института.

Зависимость способности к самоорганизации института от его актуальной структуры эмпирически достаточно хорошо обоснована социальными науками при полном отсутствии адекв атных математических моделей 1 . Для появления формальных моделей самоорганизации открытых иерархических структур необходим новый терминологический и понятийный аппарат, раздвигающий рамки традиционной (неиерархической) структур - ной динамики.

В качестве примера рассмотрим одно из базовых понятий динамики — устойчивость, связываемую с инвариантами изме - нений (сохранение качественной специфики при количестве н- ных вариациях). Если изменения происходят только во внешн ей среде, устойчивость системы естественно назвать статиче ской; в противоположность этому инварианты изменений самой сис темы свяжем с ее динамической устойчивостью. Последняя прим е- нительно к иерархическим структурам должна характеризо вать их способность сохраняться в процессе изменений. Меру так ого сохранения естественно связать с мерой сложности сохран яемой структуры (числом сохраняемых иерархических уровней, зве ньев, вершин, ребер и т. п.).

Распределение по структурному графу системы меры стати- ческой устойчивости его вершин играет определяющую роль в моделировании динамической устойчивости. Если статичес кая структурная устойчивость внутренних подсистем меньше, ч ем внешних, то есть их главные связи разрушаются при меньшей величине возмущений, чем аналогичные связи внешних подси с- тем, то структура разрушается «снизу вверх» или «от малог о к большому». Такую иерархическую структуру можно назвать д и- намически устойчивой. В противном случае высшие уровни мо гут разрушиться при сохранении низших, которые при этом либо деградируют вместе с ней, либо образуют новые более прост ые системы. Таким образом, введенная на качественном уровне динамическая устойчивость системы означает повышение мер ы статической устойчивости ее подсистем с ростом их иерархиче ского уровня.

291

РАЗДЕЛ II

В описанных выше адаптационных структурных изменениях оптимальность и устойчивость исключали друг друга, однак о в развивающейся системе эти свойства могут быть взаимно об условленными. Действительно, адаптация структуры к процесс у своего изменения, очевидно, означает его оптимизацию. Име нно с этим типом оптимизации целесообразно связать свойство устойчивости развития.

Покажем, что устойчивость развития есть следствие динамической устойчивости системы, увеличивающее меру после - дней. Малая статическая устойчивость, а следовательно, из мен- чивость и разнообразие внутренних подсистем (означающие высокую динамическую устойчивость системы), приводит к направленности изменений «снизу вверх», то есть к самоорган изации и устойчивости развития. При этом, чем сильнее уменьша - ется степень динамической устойчивости системы и ее слож - ность, чем больше период упрощения структуры, тем, очевидно, менее устойчивым является развитие. И, наоборот, при высокой статической устойчивости малых подсистем (в динами чески слабоустойчивой системе) первыми начинают перестраив аться подсистемы достаточно высокого иерархического уровн я. Для таких способов перестроек требуется гораздо больше врем ени и ресурсов, поэтому они характеризуются длительными перио дами хаоса, понижения динамической устойчивости, конкурентоспособности, безопасности и сложности системы. Такое ра звитие, очевидно, следует признать неустойчивым.

Качественное введение динамической устойчивости иерархических структур и устойчивости их развития отнюдь не ис - ключает количественных отношений. Предложим формализм, который может, по нашему мнению, служить базой структурной динамики больших иерархических систем. Введем простр анство состояний структуры системы. Рассмотрим множество и ерархических графов Ω. Его подмножество — множество деревьев с общим корнем и листьями — назовем монодеревом, а каждый граф этого подмножества — состоянием монодерева. Число ли с- тьев монодерева (одинаковое для всех, входящих в него графов) назовем его размерностью, число звеньев в каждом из графов — структурной размерностью последнего. На каждом монодереве введем обратимую унарную операцию элементар -

292

Дискуссионные проблемы развития институциональной теор ии

ного преобразования: поглощения (выделения) одной из глав - ных вершин подчиненного звена. В результате появляются об - щие и тупиковые состояния монодерева: для первых возможна прямая и обратная операции, а для вторых — только одна из них. Монодерево замкнуто относительно своих элементарны х преобразований. На множестве монодеревьев зададим обрат и- мую бинарную операцию суммы: результат суммирования в слу - чае отсутствия у слагаемых общих звеньев является механи ческим объединением последних, в противном случае общие звенья «склеиваются». Элементарное преобразование недерев а производится в несколько этапов: расчленение графа на деревь я путем соответствующих вычитаний; элементарное преобраз ование одного из деревьев; сложение деревьев.

Подмножество элементов Ω, образуемое некоторой совокупностью монодеревьев и графами, полученными в результа - те применения над ними двух описанных выше операций, замкнуто относительно множества последних и образует подпр остранство, структурной размерностью которого назовем коли че- ство монодеревьев в совокупности. Размерность подпростр анства равна числу различных листьев его монодеревьев. Эти подпространства назовем виртуальными адаптивными простран ствами (VA-пространствами) состояний структуры системы. Содержательный смысл вводимых терминов раскроем далее.

Сумма всех VA-пространств также замкнута относительно введенных операций и образует виртуальное пространство состояний структуры системы (V-пространство), каждой точке которого отвечает единственная иерархическая структура, хар актеризуемая двумя типами размерности — общей и структурной.

В этих пространствах зададим траектории как произвольные упорядоченные совокупности их точек. Процесс смены со - стояний в VA-пространстве (движение по VA-траекториям) назовем виртуальной адаптацией (VA-адаптацией). Можно ввести разновидности VA-адаптации, связанные с изменением структурной размерности: развивающая (при возрастании), деград и- рующая (в обратном случае), дрейфовая (без изменения). В каж - дый момент времени виртуальная система находится в одном из VA-пространств, расположенном в единственном V-простран- стве. В следующий момент времени она, вообще говоря, может

293

РАЗДЕЛ II

как оставаться в «старом», так и перейти в некоторое «ново е» VA-пространство.

Движение виртуальной системы по траекториям, переводящим ее в новое VA-пространство, можно классифицировать на виртуальное развитие (V-развитие), — в случае большей размерности нового VA-пространства, виртуальную деградацию (V-дег- радацию) — в случае меньшей размерности, виртуальный дрей ф (V-дрейф) — в случае сохранения размерности. С другой стороны, V-траектории можно разделить на диверсификационные (при сохранении базисных элементов) и инновационные (при их из - менении).

Введем пространство виртуального развития как факторпространство V/VA исходного V-пространства, элементами которого являются VA-пространства как классы смежности по неизменному базису. Таким образом, можно говорить о двух указа н- ных выше типах структурной динамики — адаптивной и динамике развития.

Для превращения описанных выше точечных пространств в фазовые необходимо ввести в них элементарную базу тополо гии. В элементарную окрестность точки VA-пространства включим все точки, получающиеся из данной в результате элементарного преобразования (простейшего акта V-адаптации). Аналогичное определение элементарной окрестности точки V/VA-пространства введем на основе определения элементарного акта V-развития (добавления в базис VA-пространства одного монодерева — расширения или сужения размерности пространства на единицу). П ри этом элементарный акт V-дрейфа можно представить как неупорядоченную пару последовательных элементарных актов — V-раз- вития и V-деградации. Элементарная окрестность в V-пространстве есть объединение двух вышеопределенных окрестностей.

Понятие элементарной окрестности может служить базой элементарной топологии во введенных пространствах, опис ываемых фазовыми графами с вершинами в точках исходного пространства и ребрами — наиболее простыми преобразованиям и. При этом непрерывные траектории естественно определить как пути в фазовых графах. Указанные выше два вида VA-динами- ки — развивающая или деградирующая — связаны с преобразованием фазовых графов в направленные, а третий вид — дрей-

294

Дискуссионные проблемы развития институциональной теор ии

фующая — отвечает ненаправленному графу. Аналогично, V-раз- витие и V-деградация связаны с введением направления на фазовом графе V/VA-пространства и направленным траекториям, а V-дрейф отвечает попеременному движению.

Переход к «траекториям» структур связан с заданием в точках V-пространства функций состояния, вид и число которых могут различаться в различных пространствах. Они определяют ло кальные и глобальные динамические свойства фазового простра нства. Например, устойчивость точек соответствующих пространств по отношению к каждому функционалу состояния и абсолютной уст ой- чивости — по отношению ко всей их совокупности можно связ ать с экстремальными свойствами последних. Каждый эмпиричес ки вводимый на каждом новом уровне моделирования функциона л определяет правило отбора траекторий, наиболее существе нно ограничивающее их многообразие. В случае метризации VA- и V-про- странств каждой траектории можно поставить в соответствие и метрический функционал (см., например: Воронин, Мишин, 2003). Совокупность всех функционалов выполняет функцию отбора т ипов динамики и траекторий. Далее приводятся примеры возможны х функционалов и соответствующие им оптимальные иерархические структуры. Дальнейшее развитие динамической модели структуры институтов требует перехода на следующие уровни моделиров ания. В связи с этим заметим, что описание динамики подсистем зам кнутой иерархической системы возможно только на уровне откр ытой системы, что позволяет дать содержательную интерпретаци ю введенным выше терминам.

§ 3. ÈНСТИТУТ — КИБЕРНЕТИЧЕСКАЯ СИСТЕМА

Размытость субъекта и механизмов управления в большинстве институтов, «мягкость» их структуры, количественная неопределенность реализуемых институций говорят об их слаб ой управляемости в традиционном понимании, то есть применительно к технологическим процессам и малым группам. Однак о одна из главных задач управления — поиск оптимальных сост ояний — имеет самостоятельное значение, выходящее за рамки собственно институционального менеджмента. Оптимальные состояния могут выступать как конечные (эквифинальные) сос то-

295

РАЗДЕЛ II

яния различных процессов (гомеостазиса, самоорганизации , развития), изучаемых на следующих уровнях моделирования.

Любая цель управления может формулироваться как задача оптимизации, поэтому определим частную задачу управлени я институтом как поиск оптимальной (для некоторого заданно го на ней функционала) иерархической структуры. Эта задача д о последнего времени находилась вне сферы внимания класси ческих «оптимизационных» направлений математики и ее эконо ми- ческих импликаций. До сих пор не только не разработаны эффективные методы решения подобных задач, но и отсутствует их постановка даже в общем виде. Не разработана и проблема кр итериев институциональной оптимальности.

При наличии только функционала состояния оптимизационную задачу можно назвать статической. Однако поскольку оптимальная структура неявным образом зависит и от изменчи вых внешних условий, актуальной является задача динамическо й оптимизации. В этом случае кроме эффективности функциониро вания структуры необходимо учитывать и затраты на ее возмож - ные перестроения. В частности, динамическая оптимизация с вязана с проблемой выбора оптимального числа уровней иерар хии в зависимости от внешних условий, которая обсуждается в м атематической литературе лишь на качественном уровне.

Изложим кратко подход к решению поставленной задачи и некоторые результаты моделирования (подробнее см.: Воронин, Мишин, 2003). Сформулируем задачу оптимизации иерархической структуры (конечного ориентированного ациклическог о гра-

фа): найти arg min P(G) , ãäå Ω — множество допустимых иерар-

GΩ

хических структур (иерархий) с заданным на нем функционалом P : Ω → [0;+∞), который будем называть функционалом стоимости. Как отмечалось выше, свойства заданных на структу ре функционалов (целевых функций) зависят от содержательны х интерпретаций, возникающих на следующих уровнях описани я, однако математический подход требует выделения их самых общих свойств. Постулируемые далее свойства функционала со держательно связаны с однородностью институциональной стр уктуры и обычно выполняются в периоды ее стабильности. Дале е будем предполагать, что функционалы аддитивны (представи мы в виде суммы стоимостей отдельных звеньев графа) и просты

296

Дискуссионные проблемы развития институциональной теор ии

(стоимости структурно эквивалентных графов — одинаковых с точностью до переименования не начальных вершин — равны).

Рассмотрим граф организации, под которой будем понимать воплощенный в реальной структуре любого типа, описыв а- емой, например, графом триад или базовыми графами, над множеством элементов N (элементарных функций, исполнителей), в котором на нижнем уровне находятся элементы из N, подчи- няющиеся вершинам последующих уровней, причем каждая гла в- ная вершина однозначно характеризуется группой (множест вом) подчиненных ей элементов.

Введем понятие графа организации заданного набора f = { f1,K, fm } групп элементов fi N , то есть графа, который содержит все группы набора. Множество таких графов органи зации обозначим через O(f). Решением задачи на O(f) будет оптимальный среди графов организации, которые организуют гру п- пы элементов из f.

Для r ³ 2 r-организацией назовем такую социальную структуру, в графе которой каждое звено имеет не более r ребер. Последовательной организацией назовем 2-организацию, в ко - торой одно из ребер каждого звена связано с листом. Органи зацией без пересечений назовем организацию, в которой любой вершине непосредственно подчинены вершины, координирую - щие и субординирующие непересекающиеся группы. Через Or(f),

~ ~

Op(f), O(f ) , Or (f ) соответственно обозначим множество r-орга- низаций, последовательных организаций, организаций без п ересечений, r-организаций без пересечений, которые входят в O(f), то есть организуют группы из набора f.

Если набор	~	будет
	f = { f } состоит из одной группы, то O(f )

множеством деревьев организации одной группы f. Через

~		~	( f )
D( f ) = O( f )	è	Dr ( f ) = Or		соответственно обозначим множе-

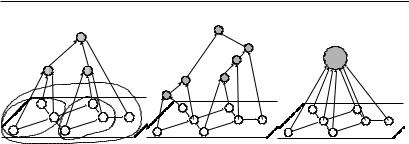
ство деревьев и r-деревьев из O(f). Веерной (двухуровневой) организацией (простой структурой) назовем организацию, в кото - рой каждая группа организуется непосредственно из соста вляющих ее элементов. Примеры видов организации приведены ниж е нарис.2.

~	Решение задачи на объединении множеств O(f), Or(f), Op(f),
	~	(f )
O	(f ) , Or		для различных наборов f получается после решения

297

g V \ NG

P(G) =

РАЗДЕЛ II

задачи на каждом из множеств по отдельности. С помощью так их объединений можно представить достаточно широкий класс множеств графов организации.

Структурный функционал на множестве организаций пред-

ставим в виде å P(g1 ,K, gk ) , ãäå G = (V , E) — организация, NG — множество листьев или начальных вершин (элементов), g1,.., gk — подгруппы, непосредственно организуемые вершиной (группой) g 2. Величина P (g1,.., gk) ³ 0 определяет стоимость звена, организующего набор групп g1,.., gk. Структурный функционал полностью определен, если величина P (g1,.., gk) задана на всевозможных наборах групп.

Функционал назовем монотонным, если его значение не убывает при расширении одной из подгрупп и при добавлении новой подгруппы. Функционал назовем выпуклым, если при k ³ 3 вместо организации подгрупп g1,..., gk в группу g = g1 K gk можно, не увеличивая стоимость, сначала организовать неко торые подгруппы из g1,.., gk, а затем полученную группу организовать с оставшимися подгруппами из g1,.., gk. Назовем функционал вогнутым, если уменьшить стоимость таким образом нельзя. Выпуклый функционал назовем существенно выпуклым, если при организации двух неначальных подгрупп можно из одной уда - лить произвольный элемент, а затем организовать его с пол у- ченной группой, не увеличивая стоимости. Справедливы след у- ющие теоремы:

Теорема 1. При монотонном функционале для любой организации G O( f ) одной группы f существует дерево D D( f ) не большей стоимости: P(D) ≤ P(G) .

Теорема 2. При выпуклом функционале для любой организации G O(f ) набора групп f существует 2-организация G2 O2 (f ) не большей стоимости: P(G2 ) ≤ P(G).

Теорема 3. При монотонном вогнутом функционале веерная организация одной группы f оптимальна на O(f).

Теорема 4. При существенно выпуклом функционале для любой организации G O(f ) набора групп f существует последо-

298

Дискуссионные проблемы развития институциональной теор ии

вательная организация Gp Op (f ) не большей стоимости:

P(Gp ) ≤ P(G).

Из этих теорем можно сделать следующие основные выводы об организации произвольного числа групп: a) при выпук-

лом функционале 2-организация минимальной стоимости буде т

~

оптимальной (решения на O2(f ) è O2 (f ) будут оптимальны соот-

~ ~

ветственно на Or(f), O(f) è Or (f ) , O (f ) ); б) при существенно выпуклом функционале последовательная организация мини мальной стоимости будет оптимальной (решение на Op(f) будет опти-

~ ~

мально и на O(f), Or(f), O(f ), Or (f )).

По поводу организации простого института из данных теорем можно сделать следующие основные выводы: a) при монотонном функционале дерево минимальной стоимости также б у- дет и оптимальной организацией (решения на D(f) и Dr(f) будут оптимальны соответственно на O(f) и Or(f)); б) при монотонном выпуклом функционале 2-дерево минимальной стоимости такж е будет и оптимальной организацией (решение на D2(f) будет оптимально и на D(f), Dr(f), O(f), Or(f)); в) при монотонном вогнутом функционале веерная организация такого института оп ти-

~

мальна на O(f), O(f ).

В качестве примера рассмотрим задачу об оптимальной орга - низации функционального взаимодействия, заданного с пом о- щью неиерархического (сетевого) графа. Между вершинами гр а- фа (элементарными функциями) идет обмен материалами, информацией, и т. п., что описывается ребрами графа и соответствующими им векторами мощности потоков. Для организации взаимодействия необходимо создание управляющих центров , координирующих потоки между элементами некоторых групп . Управляющие центры следующего уровня координируют пото ки между подчиненными группами и т. д. Затраты на управляющий центр описываются функцией затрат K(·) от суммарной мощности координируемых потоков. В результате получим задачу о б оптимальном на D(f) дереве организации со структурным функционалом стоимости P, где f = N = {a1,K, an } — множество (группа) элементов технологического графа.

299

РАЗДЕЛ II

III

I

II

14

			1	4	1		4
3	6	7
			3	6	7	3	6	7
2	5	2	5		2		5

Рис. 2. Примеры моделей организации функциональных связей в иерархии

На рис. 2 приведены различные примеры надстройки организационного графа институтов над функциональным. В цент ре приведен пример 2-организации, справа изображена веерная организация. В случае выпуклой функции затрат оптимальна 2-орг а- низация, в случае вогнутой — веерная организация (соответ - ственно, максимум и минимум управляющих центров, см. теоре - мы 2 и 3).

Введем понятие анонимного функционала, зависящего не от характеристик организуемого института, а от некоторой его объективной характеристики — сложности. Введем понятия о д- нородности (независимости от масштаба сложности) и корре ктности в нуле (стоимость добавления подструктуры нулевой сложности — нулевая) анонимного функционала. Исходя из эмпири - ческого анализа различных типов коллективной деятельно сти рассмотрим следующие примеры однородных функционалов:

P (C (g1),K,C (gk )) = [C (g1 ) + K+ C (gk ) − max( C (g1),K,C (gk ))]â (I);

P(C (g ),K,C (g

k

)) = [C (g ) + K+ C (g

k

)]â

(II);

1

1

P(C (g ),K,C(g

k

),C (g)) = (C(g) / max(C

(g ),...,C(g

k

)) −1) â

(III);

1

1

P(C (g1 ),K,C (gk ),C (g)) = (åi=

C (g) − C (gi )) â

(IV),

1,k

ãäå g = g1 ÈKÈ gk

—

организуется из подфункций g1,..., gk;

â (0;+∞) —

параметр функционала;

C(g) ³ 0

—

некоторая функция группы — сложность —

монотонная

ïî

вложению групп

300