9.1. Как работает метод дп

Для первоначального представления метода ДП не будем прибегать к математическим выкладкам и рассмотрим его сущность на описательном уровне. Представим себе лабиринт без петель, в котором между любыми входами и выходами встречается одинаковое число развилок (узлов), например 3. Во всех узлах пересекается более одной дороги. Каждому переходу в лабиринте соответствует определенное время. Необходимо найти путь от одного из входов к любому выходу, на который требуется минимальное время.

Эту задачу можно решить методом полного перебора всех маршрутов, ведущих от фиксированного входа к выходу из лабиринта. При этом число вариантов может оказаться весьма большим, а изменение входа потребует повторного перебора. Принципиально другой подход дает метод ДП. Он предлагает конструировать оптимальный путь по частям, для чего нужно представить задачу как многошаговую. Разместим условно все входы на одной вертикальной прямой, все узлы, которые встречаются первыми на пути от входов к выходам, - на другой прямой. Также поступим со второй и другими группами узлов и, наконец, с выходами. Получим схему лабиринта в виде, показанном на рис.9.2.

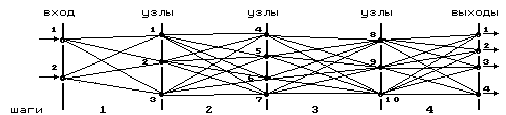
Рис. 9.2

В данном случае мы говорим, что задача представлена как 4-шаговая. Построение оптимального пути можно начинать с 1-го или 4-го шага, но предпочтительнее с 4-го. Такой порядок решения иногда называют обратной прогонкой в отличие от прямой, при которой идут с 1-го шага. Следует сразу заметить, что для некоторых задач возможен только один порядок прогонки, обусловливаемый спецификой задачи.

Итак, начнем с построения пути на 4-м шаге. Но мы тут же сталкиваемся с проблемой: как принимать решение, если не известен узел, в котором мы окажемся после оптимального прохождения первых трех этапов? Чтобы обойти эту проблему, будем искать оптимальное решение для каждого из узлов, в котором можем оказаться перед 4-м шагом (это узлы 8,9 и 10). Фиксируем узел 8 и из четырех значений времени перехода из него к выходам выбираем наименьшее. Соответствующий переход может принадлежать оптимальному пути. Узлу 8 приписываем этот переход и найденное минимальное время, которое обозначим как t₈. Аналогично поступаем, фиксируя узел 9, а затем 10. В результате получим t₉ и t₁₀ соответственно и переходы, на которых достигаются эти минимальные значения времени. Тем самым завершается первый этап построения оптимального пути. Результат представлен на рис.9.3, где жирными линиями выделены оптимальные переходы.

Теперь полагаем, что осталось совершить 3-й и 4-й переходы. Но как и ранее, мы не знаем узел, с которого будем двигаться. Это снова вынуждает нас искать решение не для одного, а для всех узлов, в которые можем прийти после первых двух шагов. Фиксируем узел 4 и определяем минимальный путь из него к выходам. При полном переборе пришлось бы сопоставлять 12 вариантов (столько путей связывает узел 4 с выходами). Однако нам достаточно сравнить только три: 1)время на переходе 4-8 плюсt₈; 2)время на переходе 4-9 плюс t₉; 3)время на переходе 4-10 плюс t₁₀. Минимальное значение приписываем узлу 4 (t₄) и выделяем жирной линией соответствующий переход на третьем шаге. Здесь уже проявилась принципиальная особенность ДП: оптимальный переход на шаге 3 определялся не как самый короткий среди переходов этого шага, а как такой, который обеспечивает минимум времени от данного узла к выходу. Это значит, что выбирая решение на 3-м шаге, мы учитывали его последствия. Точно так же находим решения для узлов 5, 6 и 7. Возможные результаты после второго этапа решения приведены на рис.9.4.

Рис. 9.4

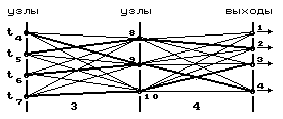
Опираясь на них, можно переходить к третьему этапу построения оптимального пути, охватывающему 2, 3 и 4-й шаги. Рассуждения аналогичны вышеприведенным. Например, оптимальный переход на 2-м шаге из узла 1 определяется по минимуму из четырех значений:

.

Переход, которому соответствует t₁ , и будет наилучшим для узла 1. И снова отметим: выбор перехода на одном 2-м шаге проводился с учетом влияния на последующие шаги вплоть до выхода! Нетрудно подсчитать, что при полном переборе путей из узла 1 к выходам пришлось бы сравнить 48 значений, каждое из которых вычисляется как сумма трех чисел. После завершения третьего этапа расчетов будут определены оптимальные пути из узлов 1-3 (рис.9.5).

Последний, четвертый, этап охватывает все шаги. Определение оптимального перехода на 1-м шаге для каждого из входов требует сравнения всего трех вариантов против 144 при полном переборе.

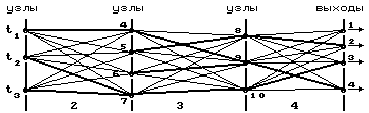
Рис. 9.5

Найдя решение для 1-го шага, мы тем самым завершаем построение оптимальных путей (рис.9.6). Непрерывная жирная линия, соединяющая заданный вход с выходом, и есть оптимальный путь, а соответствующее ему минимальное время равно t_вх. Двигаясь по нему от входа к выходу, то есть в прямом направлении (или, иначе говоря, в направлении, обратном порядку расчета), последовательно находим переходы, составляющие оптимальный путь.

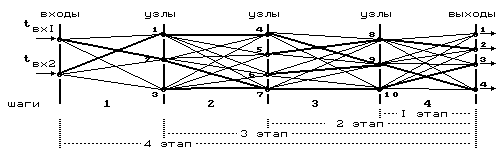
Рис. 9.6

Этот пример иллюстрирует основные черты метода ДП:

1. Вместо одной задачи решается 4 однотипных задачи меньшей размерности. Если каждому шагу поставить в соответствие одну переменную, а переходу - ее значение, то исходная задача - это задача оптимизации с четырьмя переменными. В рассмотренной процедуре расчета она заменяется последовательностью четырех задач с одной переменной, что существенно облегчает решение.

2. Решение каждой из этих задач опирается на результаты решения предшествующей (в смысле порядка расчета) задачи. Связь задач осуществляется через состояние, которое есть, с одной стороны, результат выбора конкретного перехода на данном шаге, с другой - исходная информация для извлечения результата решения непосредственно предшествующей задачи. Из такого смысла состояния следует, что каждая задача должна решаться для всех состояний, с которых может начаться рассматриваемый шаг. В нашем примере состояние полностью описывается номером узла или входа, и на каждом этапе мы искали решение для всех возможных узлов, так как иначе нельзя было бы приступить к следующему этапу расчета. Такую схему расчета называют условной оптимизацией. Это название подчеркивает, что на каждом шаге при выборе оптимального решения оговаривается условие, а именно, состояние, относительно которого ищется решение.

3. При заданном исходном состоянии, то есть для известного входа, выделение оптимальных переходов на каждом шаге не требует оговаривать условия: заданный вход определяет оптимальный переход на 1-м шаге, его результатом будет состояние накануне 2-го шага, по которому определяется оптимальный переход на 2-м шаге, приводящий в состояние, из которого совершается оптимальный переход на 3-м шаге и так до выхода. Определение оптимального решения для заданного исходного состояния по результатам условной оптимизации, осуществляемое в направлении, обратном условной оптимизации, в динамическом программировании называют безусловной оптимизацией.

4. Как видно из рис.9.6, значительная часть выделенных жирной линией переходов не входит в оптимальные пути, что на первый взгляд кажется существенным недостатком метода, так как соответствующие расчеты сделаны впустую. Однако более глубокий анализ показывает, что этот недостаток метода оборачивается его достоинством. Действительно, при реализации оптимальных решений нередки отклонения от первоначальных условий, что приводит систему в состояние, отличное от предусмотренного найденным решением. В этом случае при любом другом методе пришлось бы решать задачу заново, в то время как в результатах условной оптимизации ДП уже содержатся оптимальные решения для всех возможных состояний и поэтому достаточно выполнить лишь безусловную оптимизацию для нового состояния.

Уяснение рассмотренного примера и выводов по нему очень важно для понимания всего последующего материала.