9.8. Многомерные задачи динамического программирования

В рассмотренных выше задачах вектор состояния S имел размерность 1 или 0 (нулевая в задаче о кратчайшем пути). Если размерность вектора S (число параметров состояния) больше 1, то говорят, что задача многомерна в смысле динамического программирования. Многомерные задачи порождают определенные проблемы при реализации вычислительной схемы метода ДП. Покажем на примерах, как возникают такие задачи и с чем приходится сталкиваться при их решении.

Задача 1. Необходимо распределить два вида ресурсов в объеме X и Y соответственно между N производствами при известных функциях прибыли R_j(x_j,y_j), j=1,N. Здесь x_j, y_j - количество ресурса 1-го и 2-го вида, потребляемое j-м производством.

Запишем модель задачи:

(9.40)

(9.41)

(9.42)

(9.43)

Очевидно, что задача представима как N-шаговая (по числу производств). Для принятия решения по распределению ресурсов нужно знать их количество и число производств, участвующих в распределении. При выделении ресурсов одному из производств изменяется объем ресурсов, направляемых на остальные производства. Поэтому состояние характеризуется двумя параметрами: количеством ресурса 1-го вида V и 2-го вида U (V£X, U£Y). Введем последовательность функций:

(9.44)

и рассмотрим k оставшихся производств (шагов), между которыми нужно распределить ресурсы в количестве V и U. Приняв решение о выделении k-му производству произвольного допустимого количества ресурсов x_k и y_k, будем иметь прибыль от этого производства R_k(x_k,y_k), а на остальные k-1 шагов останется ресурсов V-x_k 1-го вида и U-y_k 2-го вида. Следуя принципу оптимальности, распределим оставшиеся ресурсы оптимальным образом, что обеспечит максимальную прибыль от k-1 производств, то есть f_k-1(V-x_k ,U-y_k ). Прибыль же от всех k шагов составит

R_k(x_k, y_k)+ f_k-1(V-x_k, U-y_k).

Так как она зависит от двух переменных, то варьируя их в допустимой области, можно получить максимальную прибыль, которая по определению (9.44) есть f_k(V,U). Таким образом, приходим к функциональному уравнению динамического программирования:

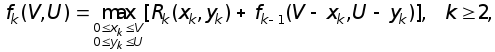(9.45)

Задача 2. Распределению подлежит один вид ресурса, но в системе имеются ограничения, связанные с его использованием. Это могут быть ограничения на общий объем, вес, габариты, стоимость и др. Рассмотрим случай двух ограничений, согласно которым фактические значения учитываемых показателей использования ресурса не могут превышать величин A и B. Тогда модель задачи можно представить в виде:

(9.46)

(9.47)

(9.48)

(9.49)

где x_i - количество ресурса, выделяемое i-му потребителю;

Z_i(x_i) - показатель эффективности i-го потребителя;

j_i(x_i), y_i(x_i) - функции ограничиваемых показателей.

Для применения метода ДП необходимо, как всегда, определить параметры состояния. Нетрудно видеть, что информация, достаточная для принятия решения на текущем шаге, должна содержать значения ограничивающих показателей. Они же непосредственно влияют на оптимальное значение эффективности системы. Кроме того, изменение ресурса на i-м шаге влечет изменение этих показателей к следующему шагу. Следовательно, в процедуре ДП ограничивающие показатели a и b выступают в качестве параметров состояния (a£A, b£B).

Определим функции последовательности как

. (9.50)

Не повторяя известных рассуждений, опирающихся на принцип оптимальности ДП, приведем в окончательном виде рекуррентное соотношение для рассматриваемой задачи:

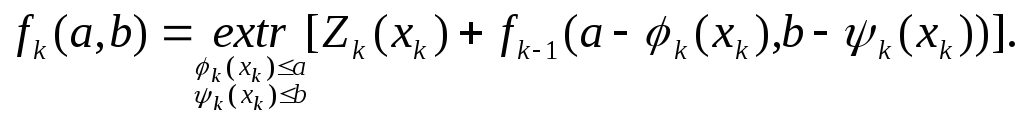(9.51)

Проанализируем полученные выражения (9.45) и (9.51). При их выводе не возникло принципиальных затруднений. Хотя число распределяемых ресурсов разное, в обеих задачах функции последовательности зависят от двух параметров состояния. Нетрудно понять теперь, что размерность вектора состояния связана с числом ограничений, включающих переменные всех шагов. Трудоемкость решения сравниваемых уравнений разная, так как различно число переменных, по которым ищется экстремум. При нелинейных функциях j_k и y_k может усложниться перебор допустимых x_k в (9.51). Однако эти различия не столь существенны, большее значение имеет одинаковая размерность вектора состояния.

Покажем на задаче 1, к чему приводит увеличение числа параметров состояния. Решение уравнения (9.45) проводится для всех возможных состояний. Число таких состояний зависит от шага дискретности и числа параметров состояния. Пусть m_x и m_y - число возможных значений ресурсов X и Y соответственно, тогда число возможных состояний будет равно m_xm_y. Для каждого из них в результирующей таблице решения уравнения (9.45) на k-м шаге должны быть представлены V, U, ,иf_k(V,U). Для вещественного числа требуется хотя бы 6 байт памяти, поэтому одна строка результирующей таблицы будет занимать не менее 30 байт. При m_x = m_y =100 число возможных состояний, а значит, и число строк составит 10^4. Следовательно, для запоминания одной таблицы потребуется около 300 Кбайт. Для эффективного расчета нужно иметь в оперативной памяти две таблицы - k-ю и (k-1)-ю. Вынос этих таблиц во внешнюю память сделает метод ДП практически малопригодным, так как затраты времени на решение задачи многократно увеличатся. Теперь нетрудно оценить, насколько будут возрастать требования к памяти с увеличением числа параметров состояния до 3, 4 и более.

Таким образом, решение многомерных задач наталкивается на проблему реализации вычислений по рекуррентным соотношениям. Сама идея метода ДП настолько привлекательна, что обнаружив трудно преодолимое препятствие применению метода в виде отмеченной проблемы, Беллман назвал ее "проклятием размерности".

Естественно, появилась необходимость найти пути решения возникшей проблемы. К предложенным средствам можно отнести использование множителей Лагранжа, аппроксимацию в области стратегий, принципиально иной способ решения рекуррентного уравнения, применение идей последовательного анализа вариантов и др. Однако ни одно из них не является универсальным, а в ряде случаев не работают все. Ниже рассматривается один из способов преодоления проблемы размерности, нашедший практическое применение.