2. Задача организации выпуска m видов продукции

Фирма ежемесячно выпускает m видов продукции, на которые имеется равномерный спрос. По каждому виду продукции известны:

С_1i - затраты на хранение единицы продукции i-го вида в единицу времени;

С_2i - затраты на запуск в производство одной партии i-го вида;

R_i - месячный спрос на продукцию i-го вида.

Для выпуска одной партии требуется один цикл производства. Изменение числа партий приводит к изменению затрат на производство одного и того же количества продукции. В течение месяца фирма может организовать не более N циклов. В этих условиях нужно так организовать производство, чтобы при полном удовлетворении спроса обеспечить минимальные затраты фирмы.

При построении модели примем одно допущение, обусловленное отсутствием необходимых данных и не имеющее принципиального значения: время выпуска партии много меньше продолжительности цикла и поэтому им можно пренебречь. График изменения уровня готовой продукции на фирме представлен на рис.9.9,

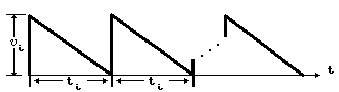
Рис. 9.9

где - объем партии продукцииi-го вида; t_i - продолжительность цикла по i-му виду продукции (в долях месяца).

Критерий, суммарные затраты на все виды продукции, определим следующим образом. Затраты на хранение и выпуск партии i-го вида продукции за время одного цикла составят

а так как количество циклов, необходимое для выпуска продукции в объеме R_i

то затраты на весь объем продукции i-го вида запишутся в виде

.

Суммируя затраты по всем видам продукции, получим критерий задачи

. (9.14)

Добавив к выражению критерия очевидные ограничения

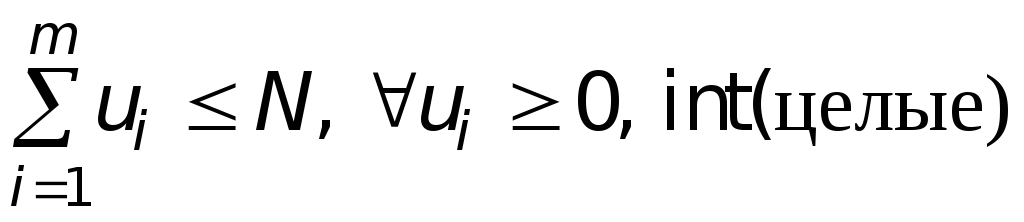, (9.15)

завершаем построение модели задачи.

По структуре эта модель аналогична рассмотренной в предыдущем разделе, так что применимость метода ДП к задаче (9.14),(9.15) не требует дополнительных доказательств. В качестве параметра состояния здесь следует взять n - максимальное количество циклов, которое может быть организовано для выпуска продукции (1nN), а за шаг примем организацию выпуска одного вида продукции. Построив из видов продукции последовательность, порядок следования в которой определяется из соображений, приведенных в предыдущем разделе, приходим к m-шаговой задаче.

Введем последовательность функций {f_n(n)}, так, что каждая функция определяется как минимальные затраты на выпускk видов продукции в заданных количествах при условии, что можно организовать до n циклов, то есть

. (9.16)

Здесь опущен индекс у параметра состояния n, так как он совпадает с индексом функции и поэтому не обязателен. Как и в предыдущей задаче, выделив из k видов (k>1) k-й и все остальные k-1 видов продукции и применив принцип оптимальности, получим затраты на k видов

Q_k(u_k) + f_k-1(n-u_k).

В этом выражении новое состояние определяется через исходное n и число циклов u_k на выпуск k-го вида продукции: на k-1 видов остается n-u_k циклов (имеем очевидное уравнение состояния n_k-1=n_k –u_k ).

Так как для фиксированного n затраты зависят только от u_k, то минимизируя их по u_k в области допустимых значений, приходим к рекуррентному соотношению

. (9.17)

Почему же в этой формуле такое ограничение сверху на u_k? Дело в том, что выпуск продукции оговорен величиной R_i, поэтому, чтобы обеспечить выпуск k-1 видов продукции, нужно иметь хотя бы по одному циклу на каждый вид и, следовательно, максимальное число циклов на k-й вид равно n-(k-1).

Первая функция вычисляется непосредственно по определению (9.16):

. (9.18)

Для численного примера ограничимся тремя видами продукции и N=7. Остальные данные следующие:

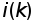
	1	2	3
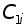
	1	2	1
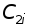
	10	8	5
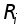
	320	200	490

Условная оптимизация начинается с вычисления функции f₁ согласно формуле (9.18). При этом можно воспользоваться классическим методом, так как требуется найти минимум дифференцируемой функции на интервале. Приравняв первую производную выражения в скобках правой части (9.18) нулю, найдем стационарную точку

.

С учетом ограничений на u₁ оптимальное решение будет иметь вид

(9.19)

где []- целая часть . По исходным данным получаем =9. Подставив в (9.18) исходные данные и оптимальное u₁, приходим к расчетной формуле

,

по которой с учетом (9.19) составляем табл. 9.1.

 Таблица 9. 1

	1	2	3	4	5	6	7
	1	2	3	4	4	4	4
	170	100	83,3	80	80	80	80

На втором шаге расчет ведем по рекуррентной формуле (9.17):

(9.20)

где .

Находить минимум в (9.20) будем перебором допустимых u₂. Для удобства ручных расчетов в промежуточную таблицу (табл. 9.2п) предварительно внесем во второй столбец значения Q₂(u₂) для всех возможных u₂ и во вторую строку значения f₁(n), взятые из табл. 9.1. Для отыскания минимума сначала фиксируем состояние, то есть значение n, а затем ведем перебор u₂. Начнем с n=1. Расчет выпуска двух видов продукции в этом случае теряет смысл, так как на 2-й вид не остается ни одного цикла - во всех клетках столбца с этим значением n ставим прочерк. Берем n=2. При этом возможен только один вариант: на 2-й вид продукции отводится один цикл. Соответствующие затраты составят

Q₂(1) + f₁(2-1)=208+170=378,

они записываются в клетку на пересечении строки с u₂=1 и столбца с n=2. Очевидно, что эти значения затрат и числа циклов являются оптимальными относительно состояния n=2 и поэтому их записываем в клетки нижних строк как значения u₂^* и f₂(n). Теперь фиксируем n=3 и вычисляем затраты для двух допустимых значений u₂:

при u₂=1 Q₂(1) + f₁(3-1)=208 + 100=308,

при u₂=2 Q₂(2) + f₁(3-2)=116 + 170=286.

Минимальными являются затраты при u₂=2, поэтому f₂(3)=286 и u₂^*=2, что и записываем в соответствующие клетки нижних строк.

В табл. 9.2п обнаруживается свойство, обусловленное структурой формулы (9.20), которое позволяет вести расчет по простой схеме прямо в таблице, не обращаясь каждый раз к формуле (9.20): для подсчета затрат в текущей клетке нужно складывать значение из 2-го столбца данной строки со значением, взятым из строки f₁ в клетке, в которую попадаем, двигаясь по диагонали от текущей клетки.

Таблица 9.2п

		n
U2	Q2(u2)	1	2		3		4		5		6			7
		f1(n)
		170	100		83,3		80		80		80			80
1	208	-	208 170 378		208 100 308		208 83,3 291,3		208 80 288		208 80 288			208 80 288
2	116		-		116 170 286		116 100 216		116 83,3 199,3		116 80 216			116 80 216
3	90,7					-		90,7 170 260,7		90,7 100 190,7		90,7 83,3 174,0	90,7 80 170,7
4	82							-		82 170 252		82 100 182	82 83,3 165,3
5	80									-		80 170 250	80 100 180
6	81,3											-	81,3 170 251,3
		-		1		2		2		3		3	4
		-		378		286		216		190,7		174	165,3

Аналогично проводим расчет для n от 4 до 7 включительно, занося получающиеся значения в табл. 9.2п. Этим завершается расчет на втором шаге. Результаты сохраняются в виде табл. 9.2.

 Таблица 9.2

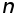
	1	2	3	4	5	6	7
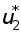
	-	1	2	2	3	3	4
	-	378	286	216	190,7	174	165,3

Теперь переходим к третьему шагу расчета, которому соответствует рекуррентная формула

(9.21)

где .

Как и на предыдущем шаге, вычисления выполним в промежуточной таблице (табл. 9.3п), в которую переносятся значения f₂ из табл. 9.2 и предварительно рассчитанные значения Q₃(u₃). Схема расчета полностью идентична 2-му шагу, но расчет по трем видам продукции приобретает смысл начиная с n=3.

Таблица 9.3п

		n
U3	Q3(u3)	2	3	4	5	6	7
		f2(n)
		378	286	216	190,7	174	165,3
1	250	-	250 378 628	250 286 536	250 216 466	250 190,7 440,7	250 174 424
2	132,5		-	132,5 378 510,5	132,5 286 418,5	132,5 216 348,5	132,5 190,7 323,2
3	96,7			-	96,7 378 474,7	96,7 286 382,7	96,7 216 312,7
4	81,2				-	81,2 378 459,2	81,2 286 367,2
5	74					-	74 378 452
		-	1	2	2	2	3
		-	628	510,5	418,5	348,5	312,7

Как и выше, можно пользоваться формальным правилом подсчета затрат без обращения к рекуррентной формуле. Из табл. 9.3п получаем табл. 9.3, которую необходимо сохранить. На этом заканчивается расчет 3-го шага и весь этап условной оптимизации.

Таблица 9.3

	1	2	3	4	5	6
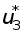
	1	2	2	2	2	3
	-	628	510,5	418,5	348,5	312,7

Далее следует безусловная оптимизация. Пусть для выпуска трех видов продукции можно организовать 5 циклов (N=5). Тогда по начальному состоянию n=5 входим в табл. 9.3 (показано стрелкой). Из нее устанавливаем, что минимальные затраты на три вида продукции составляют 418,5, при этом по 3-му виду должно быть организовано 2 цикла, то есть весь заказ выполняется двумя запусками. Согласно уравнению состояния на остальные два вида остается 3 цикла. Поэтому по состоянию n=3 входим в табл. 9.2, как указывает стрелка, и извлекаем из нее u₂^*=2, то есть весь заказ тоже делится на 2 партии. Соответствующая величина f₂(3)=286 означает затраты на 1-й и 2-й виды продукции при оптимальной организации производства. Новое состояние n=3-2=1 определяет вход в табл. 9.1, из которой берем u₂^*=1, и тем самым завершаем нахождение оптимального решения.

Действуя аналогично, нетрудно убедиться, что при N=7 оптимальное решение будет таким: минимальные затраты, равные 312,7, достигаются при u₁^*=2, u₂^*=2, u₃^*=3. Теперь ясно, что мы можем получить оптимальное решение для любых n в диапазоне от 3 до 7. Если же 3-й вид продукции будет исключен, то нам не потребуется делать полный пересчет: достаточно с заданным значением n=N войти в табл. 9.2, а затем по пересчитанному состоянию в табл. 9.1, чтобы получить соответствующее оптимальное решение. Например, для N=7 будем иметь u₂^*=4, u₁^*=3, а минимальные затраты составят 165,3. Однако, если из системы будет исключен 2-й или 1-й вид продукции, без пересчета этапа условной оптимизации уже не обойтись. Что именно надо считать заново в каждом из этих случаев, предлагается определить самостоятельно.

Анализ табл. 9.3 показывает, что с увеличением N уменьшаются минимальные затраты. Поэтому интересно посмотреть, что будет при значениях N, превышающих 7. Если расширить табл. 9.1-9.3 до n=20 по тем же формулам (9.18)-(9.21), то увидим, что наименьшие минимальные затраты равны 230 и достигаются они при N³16. Таким образом, увеличение возможного числа циклов с 7 до 16 могло бы привести к снижению затрат на 82,7. Естественно возникает вопрос: правомерно ли рекомендовать производству перейти на организацию 16 циклов? На первый взгляд кажется, что такой вариант явно выгоден и потому правомерен. Однако произойдет ли при этом реальное снижение затрат? Чтобы ответить на эти вопросы, нужно обратиться не к рекуррентным соотношениям, а к модели задачи. При построении модели предполагалось, что в пределах возможного числа циклов N используемое число циклов не влияет на затраты. Очевидно, что организация циклов сверх N потребует дополнительных ресурсов (оборудования, оснастки и пр.), то есть увеличения затрат, чего модель не учитывает. Следовательно, модель адекватна только в пределах справедливости указанного допущения и делать по ней выводы за этими пределами неправомерно. Чтобы выяснить, возможно ли снижение затрат при переходе на большее число циклов, нужно ввести в критерий статью затрат, связанную с организацией дополнительного количества циклов, и заново решить задачу.

Второй численный пример, рассматриваемый ниже, близок к задаче о лабиринте, описанной в начале главы, но имеет и свои отличия от всех ранее приведенных задач.