2. Функциональное уравнение дп

Теперь от описательного представления метода перейдем к формализованному. Рассмотрим достаточно общую многошаговую задачу, к которой применим метод ДП. Чтобы не путаться с различной нумерацией шагов и этапов расчета, пронумеруем шаги в порядке проведения условной оптимизации, в данной задаче с конца к началу. Эффективность i-го шага описывается функцией Z_i(S_i,U_i), где S_i - состояние к i-му шагу (точнее - вектор параметров состояния), U_i - управление на i-м шаге (точнее - вектор управляемых переменных или решение). Тогда структуру задачи можно представить так, как показано на рис.9.7.

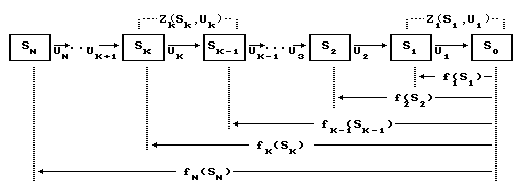
Рис. 9.7

Модель задачи ДП включает целевую функцию

, (9.1)

описание допустимой области управлений D, а также уравнение состояния , связывающее между собой два последовательных состояния. Это уравнение легко выводится из условий задачи.

Формализация вычислительной процедуры метода ДП базируется на принципе оптимальности. Напомним, что суть его состоит в том, что последующие решения должны быть оптимальными относительно состояния, сложившегося в результате предшествующих, пусть и не оптимальных, решений. Для описания этого свойства введем после­довательность функций {f_k(S_k)}, так, что каждая из них есть зависимость экстремального значения критерия заk оставшихся шагов от состояния на начало k-го шага:

. (9.2)

Какие шаги охватывает каждая функция введенной последовательности, видно также на рис.9.7. Если бы мы использовали прямую нумерацию шагов, то в формуле (9.2) суммирование должно быть от k до N, и функция f_k охватывала бы N-k шагов, что, на наш взгляд, менее предпочтительно при интерпретации ее смысла. Важно уяснить, что функции (9.2) зависят только от состояния и не могут зависеть от искомых переменных (управлений), так как по ним ищется экстремум. Отсюда также следует еще один способ определения состояния: состояние - это то, от чего зависит экстремум критерия.

Теперь построим рассуждения на основе принципа оптимальности. Предположим, что осталось k шагов (k³2), на которых предстоит принять решение, и S_k - состояние, сложившееся к k-му шагу (см. рис.9.7). Выделим один k-й шаг и из допустимых управлений на этом шаге возьмем произвольное U_k. Тогда эффективность шага составит Z_k(S_k,U_k), а состояние, в которое придем в результате такого выбора, будет S_k-1. Согласно принципу оптимальности не имеет значения, как мы попали в это состояние - последующие решения, то есть решения на оставшихся (k-1) шагах, должны быть оптимальны относительно этого состояния. Но при оптимальных решениях на (k-1) шагах будет достигаться экстремальное значение критерия за все эти шаги, которое по определению (9.2) равно f_k-1(S_k-1). Следовательно, эффективность k шагов составит

. (9.3)

Очевидно, что она не является экстремальной для k шагов, так как U_k взято произвольно. Если воспользоваться уравнением состояния, то (9.3) примет вид

, (9.4)

из чего следует, что при фиксированном состоянии S_k эффективность k шагов зависит только от управления на одном k-м шаге (здесь полезно найти аналогию с задачей о лабиринте). В этом главный смысл метода ДП. Значит, варьируя U_k в допустимой области, можно найти экстремум выражения (9.4). Но экстремальное значение за k шагов по определению (9.2) есть f_k(S_k). Таким образом, окончательно получаем

(9.5)

Выражение (9.5) называется основным функциональным уравнением динамического программирования. Чтобы подчеркнуть специфическую структуру этого выражения, его также называют рекуррентным соотношением. Действительно, согласно (9.5) одна функция последовательности вычисляется через другую, непосредственно ей предшествующую. Поэтому вычисления f_k возможны только после того, как будут известны значения f_k-1 для всех возможных состояний S_k-1. Чтобы начать рекуррентные вычисления, необходимо иметь первую функцию последовательности. Она находится непосредственно по определению (9.2) для k=1:

. (9.6)

После вычисления f₁, используя (9.5), последовательно находим f₂, f₃,...,f_N. При этом каждая функция f_k () вычисляется для всех возможных состоянийS_k. Результаты вычислений представляются в таблицах одинаковой структуры, включающей состояние, условно оптимальные значения переменных (компоненты вектора U_k^*) и значение функции. Число строк в таблице равно числу состояний, возможных к данному шагу. Следует заметить, что в процессе расчета f_k допустимое множество D_k изменяется, так как оно зависит от состояния S_k, на что будет обращено внимание в следующих задачах.

Теперь по заданному состоянию S_N^{^} входим в N-ю таблицу и из нее извлекаем U_N^* и f_N(S_N^{^}). Зная S_N^{^} и U_N^*, по уравнению состояния находим S_N-1^{^} и по нему входим в (N-1)-ю таблицу, откуда берем U_N-1^* и f(S_N-1^{^}). Этот прямой ход, соответствующий безусловной оптимизации, продолжаем аналогичным образом вплоть до 1-й таблицы, из которой найдем U_i^* и f_i(S_i^{^}). Очевидно, что f_N(S_N^{^}) - это и есть оптимум нашей задачи, а соответствующие U₁^*, U₂^*,...,U_n^* - ее оптимальное решение. Таким образом, метод ДП позволил заменить задачу с N векторами переменных N задачами с одним искомым вектором каждая, что существенно облегчило решение.

Исходя из всего вышерассмотренного, можно представить процедуру динамического программирования в виде следующей последовательности.

1. Имея описание и модель задачи, выделяем шаги и производим их нумерацию с конца.

2. Определяем параметры состояния и вводим последовательность функций {f_k(S_k)}, , в которой каждая функция f_k(S_k) есть наилучшее значение критерия за k оставшихся шагов относительно состояния S_k.

3. На основе принципа оптимальности составляем функциональное уравнение ДП и отдельно выражение для f₁.

9. Проводим условную оптимизацию, последовательно вычисляя f₁, f₂,...,f_N. При этом на каждом шаге для всех возможных значений состояния S_k запоминаются значения U_k^* и f_k (в таблице или файле).

5.Исходя из заданного состояния S_N^{^}, проводим безусловную оптимизацию по схеме:

S_N^{^}®табл.N®U_N^*®у.с.®S_N-1^{^}®табл.N-1®U_N-1^*®у.с.®...®S₁^{^}®табл.1® U₁^*,

где у.с. - уравнение состояния. Значение f_N(S_N) из N-й таблицы есть оптимальное значение критерия задачи.

Отметим, что при прямой нумерации шагов рекуррентная формула (9.5) связывала бы f_k с f_k+1, а в процедуре ДП следовало бы заменить нумерацию элементов и таблиц на обратную.

В следующих разделах процедура ДП будет применяться к конкретным задачам исследования операций.