9.5. Задача о кратчайшем пути

Дан сетевой график, в котором каждой дуге поставлена в соответствие ее длина L_ij (рис. 9.10). Порядок нумерации вершин не имеет значения, но в приведенной нумерации задача состоит в определении кратчайшего пути из вершины 1 в вершину 7. Подобные задачи возникают непосредственно при сетевом планировании и управлении, при определении стратегии аренды оборудования, прокладке маршрутов и в других случаях.

Рис.9.10

Модель задачи включает критерий - длину искомого пути

, (9.22)

где - путь от вершины 1 к вершине 7, и граф сети (или описывающую его матрицу). Применение метода ДП правомерно, так как задача представима как многошаговая: искомый путь есть допустимая графом последовательность дуг, а выбор дуги рассматриваем как один шаг задачи. В отличие от предыдущих задач здесь нет параметра состояния, состояние полностью определяется номером вершины, а число шагов от конкретной вершины до 7-й неоднозначно. Учитывая эти особенности, вводим последовательность функций {f_i}, i=1,7 так, что каждая функция есть минимальная длина пути от i-й вершины в 7-ю:

, (9.23)

где - множество всех допустимых путей изi-й вершины в 7-ю.

Для составления функционального уравнения возьмем произвольную вершину i (i¹7) и будем определять путь из нее в вершину 7. Из этого пути выделим один шаг - выбор вершины, следующей за i-й. Множество дуг, выходящих из вершины i, обозначим . Взяв произвольную дугу из множества , окажемся в смежной вершине j, длина пути до которой равна L_ij. В соответствии с принципом оптимальности последующее поведение должно быть оптимальным, то есть путь от j-й вершины к 7-й должен иметь минимальную длину, которая согласно (9.23) есть f_j. В результате, длина пути от i-й вершины до 7-й будет равна L_ij + f_j. Так как она зависит только от j, то выбором j можно ее минимизировать. Но минимальная длина пути от i-й вершины к вершине 7 есть по определению функция f_i. Таким образом, приходим к рекуррентному соотношению задачи:

. (9.24)

Принципиальное отличие полученного соотношения состоит в том, что в нем нет однозначной последовательности шагов, которая выражалась в предыдущих задачах равенством j=i-1 (или j=i+1), и, следовательно, число шагов из фиксируемой вершины заранее определить нельзя (действительно, путь между двумя несмежными вершинами может состоять из разного числа дуг).

Рассуждения, которые привели к соотношению (9.24), подсказывают, что начинать условную оптимизацию следует с определения f₇. Так как f₇ - минимальная длина пути из вершины 7 в саму себя, то f₇=0. Как показывает формула (9.24), вычислять можно те функции f_i, для которых уже известны все f_j, ijÎ. Поэтому следующей можно находить только функциюf₆:

f₆ = min (L₆₇ + f₇)=1+0=1.

Далее производим вычисления в порядке, диктуемом графом сети:

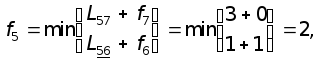
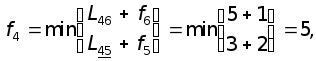
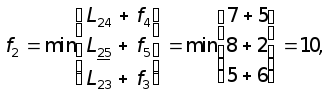
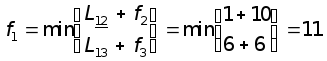
В приведенных формулах подчеркнуты индексы, на которых достигается минимум. Из расчета видно, что длина кратчайшего пути из вершины 1 в вершину 7 равна 11. Сам оптимальный путь найдем, как обычно, просматривая результаты условной оптимизации в обратном порядке: из f₁ следует, что первая часть пути лежит на дуге 1-2, значит, новое состояние - это вершина 2; из f₂ находим следующую часть пути - дугу 2-5 и очередное состояние - вершину 5; поэтому далее обращаемся к f₅ и достраиваем оптимальный путь дугой 5-6 и, наконец, заканчиваем дугой 6-7. Таким образом, построен весь путь: 1®2®5®6®7. При этом на этапе безусловной оптимизации просматривались не все функции f_i, что отличает данную задачу от ранее рассмотренных.

Очевидно, имея результаты условной оптимизации, можно легко найти кратчайшие пути из любой вершины сети в вершину 7, что характерно для метода ДП.

Для самостоятельного изучения предлагается такой вопрос: возможно ли применение метода ДП в случае, когда сеть содержит цикл, например, при добавлении дуги 6-2? Если нельзя, то почему, а если можно, то как построить расчет.