9.7. Усложненная задача

Выше рассматривались задачи, в которых метод ДП позволял переходить от исходной задачи с N переменными к N одномерным задачам. Однако могут быть и более сложные случаи. Покажем это на примере задачи распределения ассигнований в некоторой крупной корпорации.

Корпорация включает N предприятий, производящих продукцию с номенклатурой m_j каждое (j=). Прибыль, приносимаяi-й продукцией j-го предприятия, определяется по известной зависимости , гдеx_ij - объем выделенных ассигнований. Задача состоит в оптимальном распределении ассигнований в размере A между предприятиями и видами продукции при условии, что предприятию может быть выделено на все виды продукции не более B_j средств.

Критерием оптимальности здесь является суммарная прибыль корпорации. Прибыль j-го предприятия

. (9.29)

Тогда модель задачи запишется в виде:

(9.30)

(9.31)

(9.32)

(9.33)

Ограничения (9.32) связывают переменные, относящиеся к одному предприятию. Поэтому в качестве шага берем выделение ассигнований одному предприятию, и задача становится N -шаговой. При этом состояние определяется только величиной ассигнований a (a£A), распределяемых между рассматриваемыми предприятиями. Ассигнования B_j не могут быть параметрами состояния, так как их значения на последующих шагах не зависят от решения на текущем шаге. Таким образом, функции последовательности будут зависеть от одного параметра состояния:

(9.34)

и представлять собой максимальную прибыль k предприятий при суммарных ассигнованиях в пределах a. Рассуждения на основе принципа оптимальности приводят к следующему рекуррентному соотношению:

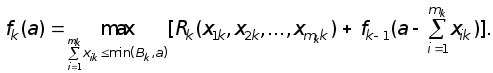(9.35)

Существенное отличие этого соотношения от рассмотренных в предыдущих разделах состоит в том, что правая часть зависит более чем от одной переменной (в данном случае от m_k переменных) и поэтому придется искать условный максимум функции многих переменных. В результате решение задачи значительно усложняется.

Облегчить решение можно с помощью декомпозиции задачи подобно тому, как было сделано в примере на применение множителей Лагранжа (гл.3). Согласно такому подходу сначала найдем параметрические оптимальные решения для каждого предприятия в отдельности, а затем рассмотрим их совместно.

На уровне предприятия имеем такую модель:

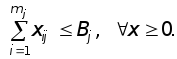
Очевидно, что данная задача может решаться также методом ДП. Она представима как m_j-шаговая с одним параметром состояния b_j (b_j£B_j). Используя представление (9.29), введем последовательность функций

,

которая подчиняется рекуррентному соотношению

(9.36)

выводимому из принципа оптимальности. Первая функция этой последовательности вычисляется непосредственно:

(9.37)

Для каждого предприятия по формулам (9.37) и (9.36) находится последовательность функций F_v^j(b_j). Зная F ^j_mj(b_j) – максимальную прибыль j-го предприятия от всех видов продукции, рекуррентное соотношение (9.35) можно представить в виде

(9.38)

для которого

(9.39)

Расчет проводим в следующем порядке. Сначала выполним вычисления по формулам (9.38) и (9.39). Имея результаты условной оптимизации (например, в виде таблиц), переходим к этапу безусловной оптимизации на верхнем уровне (на уровне корпорации). По исходному состоянию a=A входим в таблицу функции f_N(a) и находим максимальную прибыль от всех N предприятий и оптимальный объем ассигнований , выделяемый предприятиюN. В результате состояние изменяется с A на . С этим значением параметра состояния входим в таблицу функцииf_N-1(a) и извлекаем , снова пересчитываем состояние и продолжаем движение по таблицамf_k вплоть до получения . После этого проводится безусловная оптимизация на нижнем уровне. При этом каждое предприятие рассматривается независимо от других. Для примера возьмемj-е предприятие. По найденному выше значению из таблицы функцииF ^j_mj(b_j) берем прибыль j-го предприятия при оптимальном распределении ассигнований и оптимальные ассигнования на продукциюm_j. По новому состоянию входим в таблицу функции и находим

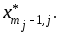
Точно так же последовательно проходим по остальным таблицам функций , в результате чего определяются всеx^*_ij. Повторив аналогичную процедуру для всех предприятий, получим оптимальное решение исходной задачи.

Как видно из формул (9.36)-(9.39), на каждом шаге условной оптимизации как верхнего, так и нижнего уровня, отыскивался максимум функции одной переменной. Такое упрощение решения явилось следствием декомпозиции исходной задачи.