3. 9.3 Сведения об эквивалентных уравнениях погрешностей

Две системы уравнений погрешностей называются эквивалентными, если им соответствует одна и та же система нормальных уравнений, а следовательно, одни и те же значения неизвестных величин. При уравнительных вычислениях иногда можно их существенно упростить путем использования эквивалентной системы параметрических уравнений поправок.

В связи с тем, что при использовании способа круговых приемов при угловых измерениях в триангуляции непосредственно измеряются направления, а не углы, уравнивание триангуляции должно выполняться по измеренным направлениям.

Предположим, что на пункте k измерены т направлений M_k-1, M_k-2, …, M_k-m на смежные пункты 1, 2, …, т.

Рисунок 9.1 – Схема измерения углов способом круговых приемов

1. Из рисунка видно, что

где _k-i – дирекционный угол стороны сети с пункта k на пункт i;

M_k-i – измеренное направление k-i;

z_k – дирекционный угол начального направления.

Введем обозначения уравненных значений _k-i, M_k-i и z_k.

,

где ’_k-i и  _k-i – приближенное значение дирекционного угла стороны сети триангуляции k-i и поправка к нему;

M’_k-i и v_k-i – измеренное значение направления k-i и поправка к нему;

z_k и  z_k – приближенное значение ориентирного угла z_k и поправка к нему.

Следовательно, для произвольного направления (т.е. для стороны k-i) можем записать уравнение в виде:

*_k-i = z*_k + M*_k-i

или

’_k-i + _k-i = z’_k +  z_k + M_k-i + v_k-i

или

–  z_k + _k-i +{(’_k-i – M’_k-i) – z’_k } = v_k-i.

Обозначим l_k-i = (’_k-i – M’_k-i) – z’_k = z’_k-i – z’_k,

где z’_k-i = ’_k-i – M’_k-i – приближенное значение ориентирного угла стороны k-i.

Тогда уравнение поправок для произвольного направления принимает вид:

–  z_k +  _k-i + l_k-i = v_k-i

На наблюдательном пункте k будем иметь систему уравнений поправок:

.

Учитывая зависимость дирекционного угла стороны от координат конечных точек:

после дифференцирования получим уравнение:

или с учетом ранее принятых обозначений:

Таким образом, на станции будем иметь систему параметрических уравнений поправок:

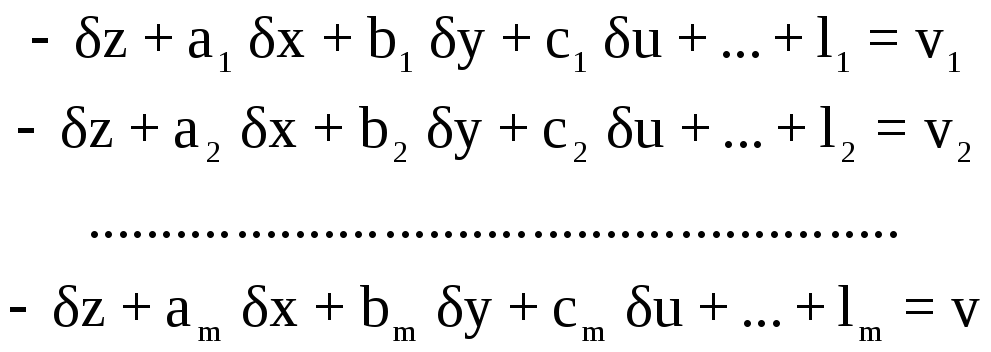
Т.е. кроме необходимых неизвестных координат определяемых точек при уравнивании триангуляции по направлениям будем иметь еще неизвестные ориентирные углы. Для их исключения используется теория эквивалентных уравнений.

Первое положение (первое правило Шрейбера).

Система т уравнений погрешностей с r+1 неизвестными:

может быть заменена системой т + 1 уравнений погрешностей с r неизвестными:

Обязательное условие – при одном из неизвестных (z) во всех т уравнениях постоянный коэффициент (в нашем случае –1). Составим систему нормальных уравнений по исходной системе уравнений поправок:

После исключения неизвестного z переходим к системе:



Если составить нормальные уравнения по второй системе, то они будут тождественны полученным, т.е. 1-я и 2-я системы параметрических уравнений поправок эквивалентны.

Второе положение (второе правило Шрейбера).

Система т уравнений погрешностей, отличающихся между собой только свободными членами и весами

a _x + b _y + … + l₁ = v₁ с весом р₁

a _x + b _y + … + l₂ = v₂ с весом р₂



a _x + b _y + … + l_т = v_т с весом р_т

может быть заменена одним уравнением:

с весом [p].

Доказывается аналогично.

Третье положение (третье правило Шрейбера).

Уравнение погрешностей

a _x + b _y + … + l = v с весом р

может быть заменено уравнением

q a _x + q b _y + … + q l = q v с весом .

Это положение используется для приведения уравнений погрешностей к весу, равному единице. Если , то получим:

с весом р = 1.