4) Свойства операций над матрицами:

1. А+В=В+А

2. (А+В)+С=А+(В+С)

3. k(A+B)=kA+kB

4. A(B+C)=AB+AC

5. (A+B)C=AC+BC

6. k(AB)=(kA)B=A(kB)

7. A(BC)=(AB)C

5) Возведение в степень. Операция возведения в степень определяется только для квадратных матриц.

А^m=A*A*…*A, m-раз

А⁰=Е, А¹=А, А^m*A^k=A^m+k , (A^m)^k=A^mk

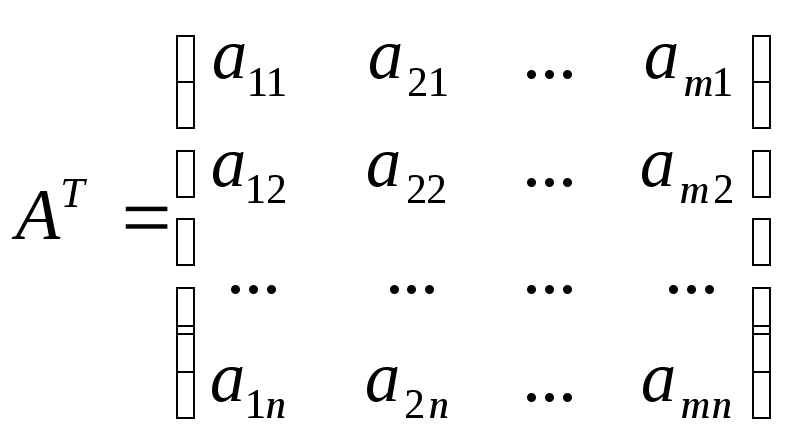
6) Транспонирование матрицы. – Переход от матрицы А к матрице А^Т, в которой строки и столбцы поменялись местами с сохранением порядка. Матрица А^Т называется транспонированной относительно матрицы А.

1.3. Определители квадратных матриц

Определителем первого порядка называется число равное элементу a₁₁.

Определителем второго порядка называется число, которое вычисляется по формуле: =a₁₁a₂₂-a₁₂a₂₁.

Определителем третьего порядка называется число, которое вычисляется по формуле:

Пример 3.

Определители четвертого и выше порядков расписывают по минорам и понижают порядок на единицу.

Минором М_ij элемента а_ij матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-ой строки и j-го столбца.

Алгебраическим дополнением А_ij элемента а_ij матрицы n-го порядка называется его минор, взятый со знаком (-1)^i+j: (А_ij=(-1)^i+jM_ij)

т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца (i+j) – четное число, и отличается от минора знаком, когда (i+j) – нечетное число.

Свойства определителей.

1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.

2. Если все элементы какой-либо строки (столбца) матрицы умножить на число к, то ее определитель умножится на это число.

3. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

4. При транспонировании матрицы ее определитель не изменяется.

5. Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.

6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.

7. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженное на одно и то же число не равное нулю.

8. Определитель произведения двух квадратных матриц равен произведению их определителей: С=А*В, где С=А*В; А и В –матрицы n-го порядка. (причем А*ВВ*А; А*В=В*А)

1.4. Обратная матрица

Матрица А^-1 называется обратной к квадратной матрице А, если выполняется:

А*А^-1=А^-1*А=Е (где Е – единичная матрица).

Обратную матрицу можно искать только для квадратных матриц и определитель этой матрицы должен быть отличен от нуля.

Если определитель отличен от нуля, то матрица называется невырожденной (при А=0 – вырожденной).

Теорема: (необходимое и достаточное условие существования обратной матрицы). Обратная матрица А^-1 существует и единственна тогда и только тогда, когда исходная матрица невырожденная.

Схема вычисления обратной матрицы.

1. Находим определитель матрицы А. Если матрица А вырожденная, то обратной матрицы не существует.

2. Находим транспонированную матрицу А^Т к матрице А.

3. Находим алгебраические дополнения элементов транспонированной матрицы А^Т_ij (i=1..n, j=1..n) и составляем из них присоединенную матрицу:

4. Вычисляем обратную матрицу по формуле:

5. Проверка А^-1*А=А*А^-1=Е

Пример 4. Найти матрицу, обратную к данной:

Решение:

1. А=14 , т.к. А0, то матрица А невырожденная.

2. нашли транспонированную матрицу.

3. 

, А₁₃=8, А₂₁-13, А₂₂=8, А₂₃=-11, А₃₁=-5, А₃₂=2, А₃₃=-1.

А_ij равно (-1)^i+j умноженное на определитель матрицы, полученной из транспонированной матрицы вычеркиванием в ней i-ой строки и j-го столбца.

4. 

5.