Свойства функций, непрерывных в точке:

1. Если функции f(x) и (х) непрерывны в точке х₀, то их сумма f(x)+(х), произведение f(x)(х) и частное f(x)/(х) (при условии (х₀)0) являются функциями, непрерывными в точке х₀.

2. Если функция у=f(x) непрерывна в точке х₀ и f(x₀)>0, то существует такая окрестность точки х₀, в которой f(x)>0.

3. Если функция у=f(u) непрерывна в точке u₀, а функция u=(x) непрерывна в точке u₀=(x₀), то сложная функция y=f((x)) непрерывна в точке х₀

Пример 7. Дана функция

Найти ее точки разрыва и исследовать их характер.

Решение: Числовая ось, являющаяся областью определения функции y=f(x), разбита на три промежутка (-, о], (0,/2), [/2, +), в каждом из которых f(x) задана соответственно элементарными функциями: (х)=2-х, (х)=cosx, (x)=0. Внутри каждого из указанных промежутков эти функции определены и, следовательно, непрерывны. Таким образом, остается исследовать функцию f(x) на непрерывность только в точках x=0 и х=/2, в которых «стыкуются» области определения функций, составляющих функцию y=f(x).

Так как f(x)=2-х при х0, то .

Далее, так как f(x)=cosx при 0<x</2, то . Следовательно,х=0 точка разрыва первого рода; в ней функция y=f(x) претерпевает скачок. Односторонние пределы функции y=f(x) в точке х=/2 таковы: (т.к.f(x)=cosx при 0<x</2); (т.к.f(x)=0 при x/2). Значение функции f(x) в точке x=/2 равно f(/2)=0. Отсюда следует, что в этой точке функция f(x) непрерывна, так как выполняются все три условия непрерывности.

Итак, функция y=f(x) непрерывна на всей числовой оси за исключением точки x=0, в которой она претерпевает разрыв первого рода – скачок.

Вопросы и упражнения для самопроверки.

1. Предел числовой последовательности.

2. Предел функции в бесконечности и в точке.

3. Бесконечно малые и бесконечно большие величины. Их свойства и связь.

4. Основные теоремы о пределах.

5. Первый и второй замечательный предел.

6. Непрерывность функции в точке, свойства. Точки разрыва.

7. Найти предел:

8. Найти предел:

9. Найти предел:

10. Является ли данная функция непрерывной в точке х=1? Если нет, то установите характер точки разрыва. .

11. Является ли данная функция непрерывной в точке х=1? Если нет, то установите характер точки разрыва.

III. Дифференциальное исчисление

1 Производная

1.1. Понятие производной

Понятие производной является одним из фундаментальных понятий математики. Многие зада­чи, как самой математики, так и естествознания и техни­ки приводят к этому понятию.

Пусть функция y=f(x) определена в промежутке X. Возьмем из этого промежутка фиксированное значение аргумента х и придадим ему приращение х так, чтобы новое значение аргумента х+х принадлежало этому промежутку. Тогда значение функции f(x) заменится новым значением f(x)+y=f(x+x), т.е. функция по­лучит приращение у=f(x+x)-f(x).

Предел отношения приращения функции у к вы­звавшему его приращению аргумента х при стремле­нии х к нулю, т. е.

называется производной функции y=f(x) по аргументу х в точке х.

Производная обозначается одним из символов: у_х, а ее значение при х=х₀ обозначается

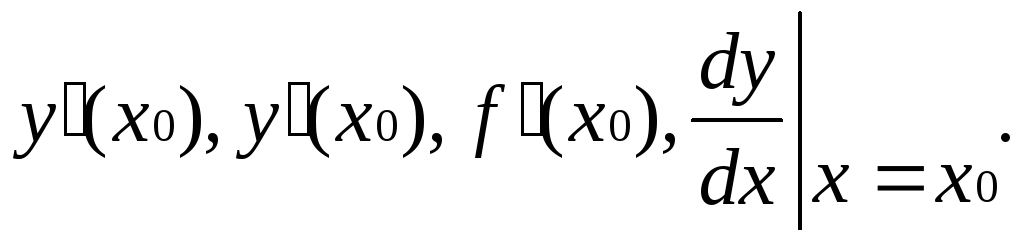
Операция нахождения производной называется диф­ференцированием.

Если функция f(x) имеет производную в точке х, то она называется дифференцируемой в этой точке.

Если функция f(x) имеет производную в каждой точ­ке промежутка X, то говорят, что эта функция диффе­ренцируема на этом промежутке.