2.3. Метод обратной матрицы

Систему (1) перепишем в матричной форме: А*Х=В, (2)

где ;;

умножим обе части уравнения (2) на А^-1 слева: А^-1*А*Х=А^-1*В,

получаем Х=А^-1*В, где А^-1 – обратная матрица к матрице А.

Пусть 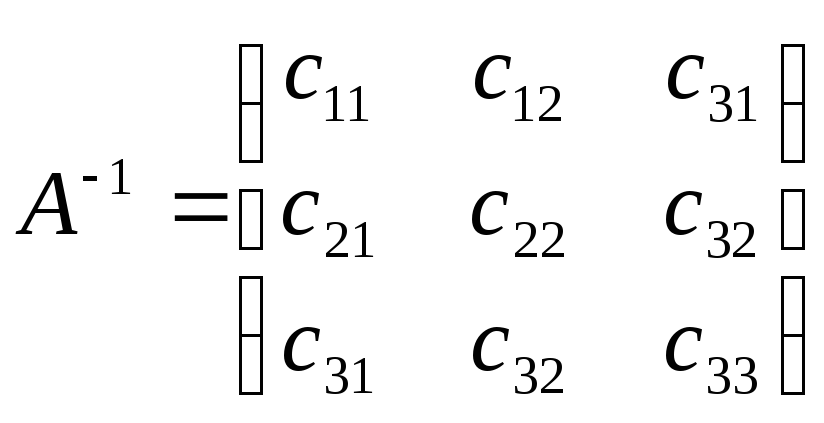, тогда

или x₁=c₁₁b₁+c₁₂b₂+c₁₃b₃, x₂=c₂₁b₁+c₂₂b₂+c₂₃b₃, x₃=c₃₁b₁+c₃₂b₂+c₃₃b₃ являются решениями системы (1).

Пример 6. Решить систему методом обратной матрицы:

Решение: Перепишем систему в матричной форме: А*Х=В, где

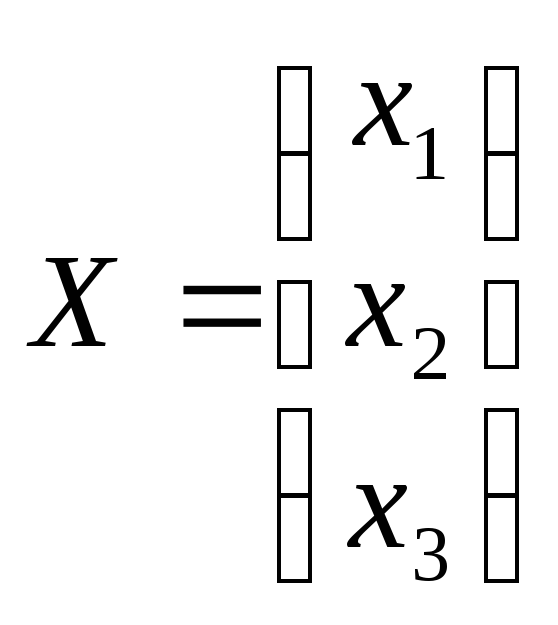, ,, Х=А^-1*В

А^-1- обратная матрица к матрице А. (см. пример 4)

,

Ответ: х₁=-1, х₂=1, х₃=0.

2.4. Метод Гаусса

Метод Гаусса – метод последовательного исключения неизвестных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе уравнений ступенчатого вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

С помощью метода Гаусса можно решить любую систему или показать, что система не разрешима.

После приведения системы к ступенчатому виду:

А) Если число уравнений равно числу неизвестных, то система имеет единственное решение.

В) Если число уравнений меньше числа неизвестных, то система имеет множество решений.

Пример 7. Решить систему уравнений методом Гаусса:

Решение. Выписываем расширенную матрицу ,(поменяем местами первую и третью строки) , (из второй строки поэлементно вычитаем первую строку, умножаем на 3 и записываем вместо второй строки). Остальные аналогично.

(третью строку умножим на 7, вычитаем поэлементно вторую строку и результат записываем вместо третьей строки). Аналогично с четвертой строкой.



Перепишем в виде системы:

Система не разрешима, т.к. 0-11.

Ответ: нет решений.

Пример 8. Решить систему методом Гаусса:

Решение. Выписываем расширенную матрицу: 



, из третьего уравнения системы находим х₃=0, подставляем во второе: –х₂+11*0=-1,  х₂=1

Подставим х₂=1, х₃=0 в первое уравнение: х₁+1-3*0=0,  х₁+1=0, х₁=-1

Ответ: х₁=-1, х₂=1, х₃=0

Вопросы и упражнения для самопроверки.

1. Что такое матрица? Какие матрицы вы знаете?

2. Операции над матрицами. Какие матрицы можно складывать, умножать? Что такое транспонирование матрицы? Свойства операций над матрицами.

3. Определители квадратных матриц. Что такое минор и алгебраическое дополнение матрицы? Свойства определителей.

4. Что такое обратная матрица? Необходимое и достаточное условие существования обратной матрицы. Схема нахождения обратной матрицы.

5. Ранг матрицы. Элементарные преобразования над матрицами. Теорема о ранге матрицы.

6. Системы линейных уравнений. Метод Крамера.

7. Метод обратной матрицы.

8. Метод Гаусса.

9. Теорема Кронекера-Капелли.

10. Решить систему уравнений всеми тремя способами:

11. Решить систему уравнений всеми тремя способами:

12. Решить систему уравнений всеми тремя способами:

13. Решить матричное уравнение:

14. Решить матричное уравнение:

15. Решить матричное уравнение: A*X*B=C, если ,,.

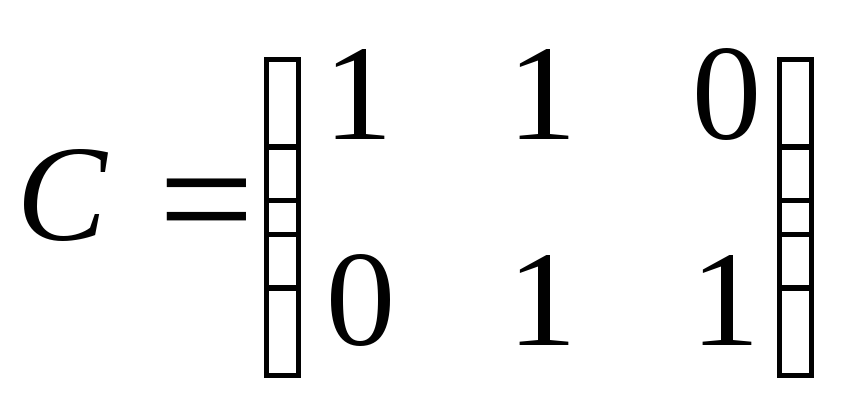II. Введение в математический анализ

1. Множества. Отображение. Функция

Множество принадлежит к числу исходных неопределенных понятий, на его основе строятся все, без исключения, математические конструкции. Множество разъясняют и как совокупность произвольной природы, рассматриваемую как единое целое. Объекты, составляющее множество, называются его элементами. Если элемент а входит в множество А то это обозначается: а  А (читается: «а» принадлежит А), в противном случае пишут а  А («а» не принадлежит А)

Некоторые множества имеют общепринятые обозначения: N – множество натуральных чисел, R – множество действительных чисел.

К основным теоретико-множественным операциям относятся:

1. Объединение (сумма) АВ={х: хА и хВ}

2. Пересечение (произведение) АВ: {х: хА и х В}

3. Разность А\В = {х: хА и х В}

Все рассматриваемые множества являются частями некоторого множества -универсума U. Тогда операция дополнения определяется следующим образом.

4. = U\ А или= {х: х А}

Определение 1. Отношение между элементами множеств Х и Y называется отображением Х в Y, если каждому элементу х множества Х соответствует только один элемент y множества Y.

Определение 2. Отображение множества Х на множество Y называется взаимно однозначным, если каждому элементу х из множества Х, соответствует единственный элемент y из множества Y, а каждый элемент y из множества Y соответствует только одному элементу x из множества X.

Определение 3. Два множества называются равномощными, если существует взаимно однозначное отображение множества Х на множество Y.

Определение 4. Числовой функцией называется отображение f числового множества X на множество R действительных чисел. Множество Х называется областью определения функции f. Если f - функция, то образ элемента х из множества Х обозначают f(x) и называют значением функции в точке х, а х называют аргументом функции.

Пример 1. Если А - множество положительных чисел, а В – множество нечетных положительных чисел, то АВ определяет множество натуральных чисел, т.е. N={1,2,3,…n…}.

Пример 2. Если А - множество всех чисел, делящихся на 2, а В – множество всех чисел, делящихся на 5, то АВ определяет множество всех чисел, делящихся на 2 и на 5, т.е. делящихся на 10.

Пример 3. Если А{1,2,3,4,5}, а В{3,5}, то А\В={1,2,4}, а В\А=.

Пример 4. Если А {1,2}, а В{3,-1,0}, то АВ={(1,3),(1,-1),(1,0),(2,3),(2,-1),(2,0)}.