книги по релейке часть 1 / ТОЭ / Демирчян К.С. Нейман Л. Р. Теоретические основы электротехники / Теоретические основы электротехники том 2

Ответы на вопросы, решения упражнений и задач

533

9. При отклонении зависимости Π( ) от линейной фильтр становится неидеальным и форма сигнала на его выходе в полосе его пропускания уже не будет повторять форму подаваемого на его вход сигнала, даже если коэффициент затухания фильтра равен нулю во всем диапазоне частот передаваемого через фильтр сигнала.

УПРАЖНЕНИЯ

2. Для расчета характеристических параметров используем выражения

, Ρ ln(

).

Z1ñ

Z10 Z1ê , Z 2ñ

Z 20 Z 2ê

AD

BC

C учетом соотношения

AD

Z10

последнее выражение можно преобразовать

BC

Z1ê

ê âèäó Ρ ln

Z10

Z1ê

.

Z10

Z1ê

Для цепи варианта à получаем

Z10 200(1 – 3,2j) Îì; Z1ê 200 Îì; Z20 –637j Îì; Z2ê 182 – 57,2j Îì;

Z1ñ 296 – 219j Îì;

Z2ñ 205 –277j Îì; Ρ 0,4 –0,4j.

3. Зависимости и Π находим, записывая найденную при решении упражнения 2 меру передачи в виде Ρ ( ) + jΠ( ). Для расчета зависимости ( ) при действии на входе фильтра идеального источника ЭДС и сопротивлении приемника rïð 200 Ом находим предварительно отношение U1( )/U2( ) и далее вели- чину как ln (U1/U2). Например, для фильтра варианта à получаем:( ) ln (U1/U2) 0,5 ln (4 + 5 10–2 2). На рис. Р14.3 изображены зависимости (lg ) и Π(lg ) для фильтра варианта à.

Ðèñ. P14.3

4. Искомые зависимости Z1(Zè, Zïð), Z2(Zè, Zïð) находим, используя выражения для сопротивлений Г-образного звена фильтра со стороны П- и Т-входов:

Z1Z 2

Z

Z

, Z

Z

(Z

2)

2 Z

Z

,

ñï

ïð

1 Z1 (4Z 2 )

ñò

è

1

1

2

Z è Z ïð

Z

2 Z 2 Z

Z

, Z

.

1

è

è

ïð

2

2

Z 2

Z

è

Z

ïð

è

534 Ответы на вопросы, решения упражнений и задач
5. Вариант à. Заменяя в выражении для передаточной функции
K(p)									kg1 g2
		p(C			g C							C g				kC g					) g g
p2C C	2			2					2	g	2				2					2			2
1						1								1				1			1
(здесь g1 1 r1 , g2 1 r2 ) p íà j , получаем после подстановки численных значе-
ний параметров элементов
K( )										1											.
	7,88 10 12 4								1,38 10 8 2
																	0,01
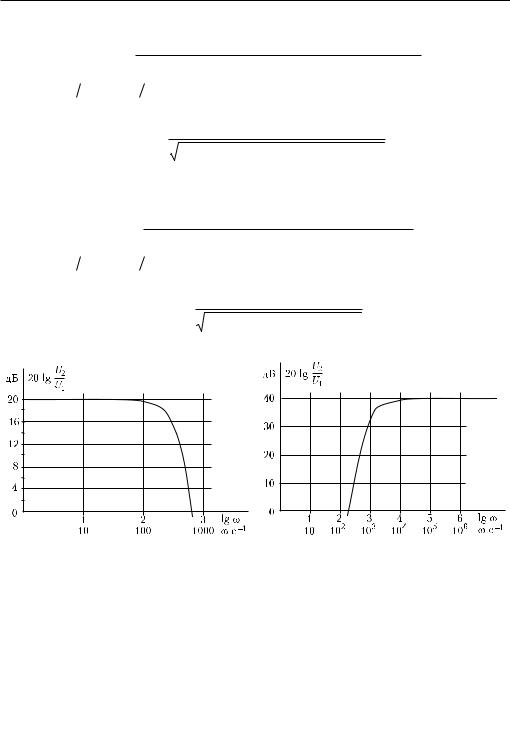
На рис. Р14.4 зависимость K( ) построена в логарифмическом масштабе.
Вариант á. Передаточная функция цепи
K(p)								kp2C C						2
												1
			p[C					C g					(1 k)C					g ] g g
p2C C		2			2	g	2					2					2					2
1										1									1		1
(здесь g1 1 r1 , g2 1 r2 ). На рис. Р14.5 построена зависимость амплитудно-час-
тотной характеристики
K( )										2
			10 4 4					29 2						126, 109
от частоты в логарифмическом масштабе.
Ðèñ. P14.4																		Ðèñ. P14.5
14.3. Электрические фильтры нижних частот типов k è m

ВОПРОСЫ

2. Так как частоты ñ среза согласованных Г-звеньев совпадают, то при увеличе- нии числа каскадно соединенных Г-звеньев участок характеристики ( ) при 0 ñ будет иметь тот же вид, а крутизна другой ее части (при > ñ) возрастет.

4. Для последовательно-производного фильтра с параметрами элементов L mL0, C mC0 имеем

	Z1 j mL0, 2Z2 j Lx +	1	,
		j mC0

Ответы на вопросы, решения упражнений и задач

535

th Ρ

Z1

4m2 L0 2

.

4(Z1Z 2 Z12 4)

4(L0 C0 2 mL0 Lõ 2 m2 L20 )

Частота среза, определяемая из условия Re (th ) 0, равна ñ

L

0 C0

.

m2 L20

mL0 Lõ

1 m2

Ïðè L

L

получаем:

L0 C0

2R0

, что совпадает с выражением

x

0

c

L2

m

L

0

для частоты среза прототипа.

5. Введение одновременно последовательного и параллельного LC-контуров в электрический фильтр улучшает его свойства за счет увеличения скорости роста затухания в полосе задерживания. Кроме того, подбором параметров контуров можно добиться большей равномерности характеристических сопротивлений фильтров, что позволяет обеспечить лучшее согласование фильтра с постоянным сопротивлением, которое во многих случаях является нагрузкой фильтра. Недостаток фильтра с двумя LC-контурами заключается в уменьшении его затухания при частотах, больших чем частоты резонанса контуров. Для увеличения затухания фильтра при больших частотах сигналов такие фильтры соединяют каскадно с фильтрами типа k, у которых коэффициент затухания неограниченно растет при .

8. Преобразование p bs изменяет параметры элементов фильтров: L bL, C bC, что ведет к изменению частоты среза фильтров c c b2 и уменьше-

íèþ â b2 раз полосы пропускания (полосы задерживания) фильтра нижних (верхних) частот.

УПРАЖНЕНИЯ

1. Частота среза равна ñ 2(LC)–0,5 2,5 105 c–1. Характеристические сопротивления цепи со стороны Т- и П-входов

									12,5
Z	ñò	12,5 1 16, 10 11 2 Îì, Z			ñï					Îì, thΡ				.
						1			16, 10 11 2			6,25 1010	2

Зависимости ( ) и Π( ) изображены на рис. P14.6 (принят логарифмический масштаб по оси ). Затухание равно 3 дБ при частоте 2,65 105 c–1, коэффициент фазы равен #/4 при частоте 1,77 105 c–1.

Ðèñ. P14.6

536 Ответы на вопросы, решения упражнений и задач

2. Используя соотношения L C 10, 2 103 , находим:

LC

L 0,02 Ãí, Ñ 2 10–4 Ô.

4. Так как частота среза фильтра оказывается равной 104 c–1, то мера передачи при 0,4 104 c–1 (в полосе пропускания) равна 0,925j, à ïðè 1,5 104 c–1 (в полосе задерживания) — Ρ 1,04 + j#/2.

Напряжение на выходе фильтра
	104 t	#
uâûõ(t) 2 sin (0,5 104t + 0,925) + 0,7 sin 15,		Â.
		2

14.4. Электрические фильтры нижних частот

УПРАЖНЕНИЯ

1. Функции f( ) изображены на рис. P14.7 ( f( ) ïðè Υ 0,5 изображена на левом графике, а при Υ 1 — на правом).

Ðèñ. P14.7

2. Так как коэффициент затухания равен нулю при частоте 0, то в силу монотонности функции f( ) в полосе пропускания наибольшее значение коэффициент затухания принимает на ее границе при 1 1. Из условия 10 lg (1 + Υ2) 3 äÁ

находим Υ 1. В общем случае при заданной величине имеем Υ

100,1 1.

3. Значение Υ2 0,58 находим из условия 20lg

1 Υ 2

2 дБ. Искомое значение

порядка фильтра получаем, решая неравенство 20lg

1 0,58 2n

; 10 äÁ, ãäå

1

1 2, n ; 2.

4. Учитывая, что амплитудная частотная характеристика rC öåïè

U 2 ( )

1

1

K( )

,

U1( )

(rC )2 1

(rC

)

2 2 1

ñ

1

ãäå		— относительная частота, и что Υ 1, находим, сопоставляя выраже-
1	c
íèÿ K( ) è f ( )				1		, соотношение между параметрами фильтра: rC 1.
					ñ

1 Υ 2 12n

Таким образом, значение одного из параметров (r èëè Ñ) можно выбрать произвольно.

Ответы на вопросы, решения упражнений и задач 537

5. Учитывая, что заданная неравномерность коэффициента затухания в полосе пропускания составляет 3 дБ, получаем, подобно рассмотренному в предыдущих упражнениях, Υ 1. Записывая передаточную функцию цепи

K(p)	U	2	(p)						2				, 2				1					1
									0										,							,
	U1(p)						p2 2 p 02							0		LC							2rC
находим ее амплитудную частотную характеристику
K( 1)												1													,
					[1 (					)2	2	]2		(2				2 )2
								ñ									ñ				2
									0		1									0		1

и приравнивая коэффициенты при соответствующих степенях частоты полино-

мов знаменателя функций K( ) è f( )			1	, получаем искомые соотноше-
1			4
			1

ния, связывающие параметры r, L, C öåïè: LC1 2c , r 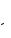2LC. Так как число пара-

метров (3) меньше числа связывающих их соотношений (2), то на их выбор можно наложить одно произвольное ограничение.

6. Амплитудная и фазовая частотные характеристики фильтра, схема которого приведена на рис. P14.8, имеют вид

K( )			k 2							,	Π( ) arctg [ b1/(b0 – 2)],
		(b 2 )2			b2
							2
	0					1
	1					1						1		1		1
ãäå b0				, b1				(1 k)
	r1C1r2C2					r1C1								C1		C2	.
												r2

Ðèñ. P14.8

14.5. Устойчивость в электрических цепях

ВОПРОСЫ

1. Корни характеристического уравнения пассивных электрических цепей лежат в левой полуплоскости (либо на оси мнимых при отсутствии в цепи резисторов). Поэтому в решения однородных дифференциальных уравнений, описывающих процессы в таких цепях, не могут входить экспоненты с положительными показателями. Цепи с зависимыми источниками могут быть как устойчивыми, так и неустойчивыми, что определяется видом цепи и соотношением между ее параметрами.

	УПРАЖНЕНИЯ	(Tp 1)k		k 1
	3. Знаменатель передаточной функции K (p)		имеет корень p
		Tp 1 k		T

при положительной и p 1T k при отрицательной обратной связи. В послед-

нем случае при любом значении коэффициента усиления k имеем ð < 0 и система всегда устойчива. Она однако теряет устойчивость при положительной об-

538 Ответы на вопросы, решения упражнений и задач

ратной связи, если k > 1. Åñëè k < 1, то система сохраняет устойчивость и при положительной обратной связи.

(a p2 a p 1)k

0

1

4. Знаменатель передаточной функции K (p)

системы имеет

a p2

a p 1

k

0

1

корни p1,2

a

a2 4a

0

(1 k)

1

1

, которые при лю-

2a0

бых параметрах системы отрицательны либо имеют

отрицательные вещественные части. Поэтому сис-

тема не может быть неустойчивой.

Годограф K1( j )

k

амплитудно-

Ðèñ. P14.9

a0 ( j )

2

a1 j 1

фазовой частотной характеристики передаточной функции K1(p) kW(p) системы с разомкнутой цепью обратной связи (рис. P14.9), проходя при увеличе- нии частоты последовательно через два квадранта плоскости, не пересекает ось Re K(j ) < 0, что означает невозможность выполнения условия –180Τ, при котором отрицательная обратная связь становится положительной и система может стать неустойчивой. Такой же ответ получаем при использовании критерия Гурвица. Усилитель, охваченный устройством отрицательной обратной свя-

зи с передаточной функцией W (p)		1		, может быть неустой-
	a p3	a p2
			a p 1
0		1	2

чивым, так как годограф K1(j ) в этом случае, проходя при увеличении частоты последовательно через три квадранта плоскости, пересекает ось Re K(j ) < 0.

	5. Записывая передаточную функцию системы K1				k	, находим, что
				Tp 1	( Π)k
	усилитель становится устойчивым при > Π –	1	.
		k

6. Искомое соотношение можем найти, анализируя зависимость корней полинома знаменателя передаточной функции от параметров элементов цепи и коэффициента усиления k усилителя. Если при некоторых соотношениях параметров хотя бы один из корней полинома знаменателя передаточной функции становится положительным (либо вещественная часть корня становится положительной), то система будет неустойчивой.

Подставляя в выражение K(p)		kZ 2 (p)		(см. решение упр. 5,
	Z1(p) Z 2 (p) kZ1(p)
§13.5) величины Z1(p) r, Z2 (p)	1	, получаем K(p)		k	. Ïðè k > 0,
	Cp		(1 k)rCp 1

когда усилитель не изменяет знака подаваемого на его вход напряжения, цепь устойчива, если 1 – k > 0, ò. å. ïðè k < 1.

7. Анализируя корни полинома знаменателя T1T2 p2 + (T1 + T2 + C2 r1)p + (1 – k) передаточной функции цепи варианта ã, приходим к выводу, что цепь будет устойчивой при условии 1 – k > 0, ò. å. ïðè k < 1. Для цепи варианта ä условие устойчивости также имеет вид k < 1.

Ответы на вопросы, решения упражнений и задач

539

8. Заменим в уравнении b p6 b p5				b				0 переменную ð íà	1	:
0		1					6		p*
b	1		b		1		b 0.
0 (p*)6			1 (p*)5					6
Умножив обе части этого уравнения на (p*)6 , получим уравнение
b	(p*)6		b		(p*)5		b 0,
6		5						0

совпадающее с исходным уравнением устойчивой системы. Так как корни Χ i è Πi
этих уравнений связаны соотношением Π										1		, то система с характеристиче-
							i
										Χ i
ским уравнением b p6	b p5	b			0 устойчива.
0	1			6
9. Миноры матрицы Гурвица
					1	0	0		0
			3
			1		2	3	1		0
			1		4	1	2		3
			0		0	1	4		1
			0		0	0	0		1

для условий варианта ã равны:
						3 1												1	0
1 3 > 0, 2										5 > 0, 3							3			– 31 < 0.
																	1 2		3
						1	2										1	4	1
Следовательно, система неустойчива.
Матрица Гурвица для варианта å такова
									3		1	0	0	0
									1		0	3	1	0
									1		4	1	0			3	.
									0		0	1	4	1
									0		0	0	0	1
		1
Имеем 1 > 0, 2	3			< 0, и следовательно, система неустойчива.
	1	0

10. Для электрической цепи варианта ã упр. 5, § 13.5 (знаменатель передаточной

функции T

T

2

p2 + (T

1

+ T

2

+ C

r

)p + 1 – k) условие положительности миноров

1

2

1

матрицы Гурвица

T1 T2 C2 r1

T1T2

0

1 k

приводит к неравенствам 1 T1 + T2 + C2r1 > 0, 2 (T1 + T2 + C2r1)(1 – k) > 0, из которых следует условие устойчивости: k < 1.

540 Ответы на вопросы, решения упражнений и задач

По выражению знаменателя (1 – k)T1T2 p2 + [(1 – k)(T1 + T2) + C1r2] p + 1 – k передаточной функции электрической цепи варианта ä упр. 5, §13.5, строим матри-

цу Гурвица

(1 k)(T1 T2 ) C1r2 T1T2 (1 k)

01 k

èзаписываем неравенства, при выполнении которых цепь устойчива:

T1T2(1 – k) > 0, 1 (1 – k)(T1 + T2) + C1r2 > 0, 2 1(1 – k) > 0. Из них следует условие устойчивости: k < 1.

11.Устойчивыми будут системы с годографами 1 и 2. Система с годографом 3

при замыкании обратной связи будет неустойчивой, так как при – # ( 0) коэффициент передачи превышает значение 1, в результате чего выполняются условия, при которых система теряет устойчивость.

12.При замыкании цепи обратной связи система с характеристикой 1 будет неустойчивой, а система с характеристикой 2 — устойчивой. Действительно, при

частоте 1 сигнала угол сдвига по фазе между сигналом на входе основной цепи и сигналом на выходе цепи обратной связи в разомкнутой системе составляет –# и величина K( 1) превышает 1. Поэтому при замыкании цепи обратной связи при 1 цепь неустойчива.

Система с характеристикой 2 будет устойчивой при замыкании цепи обратной связи, так как при 2, когда –p, имеем K( / 9 ., (20 lg K( 2) < 0).

15.1. Синтез двухполюсников

УПРАЖНЕНИЯ

1.Вариант à — коэфициент 2+j при операторе p является комплексным; варианты á è â — один из коэффициентов полинома числителя отрицательный; вариант ã — степень полинома знаменателя превышает степень полинома числителя на два.

2.Схемы электрических цепей изображены на рис. P15.1.

Ðèñ. P15.1

3. Схемы электрических цепей изображены на рис. P15.2.

Ответы на вопросы, решения упражнений и задач

541

Ðèñ. P15.2

15.2. Синтез четырехполюсников

УПРАЖНЕНИЯ

Z 22 (p)

Z 21(p)

1. à) K(p)

; á) K(p)

.

Z12 (p)

Z11(p)

2.

Òàê êàê U1(p) Z12(p)

U 2 (p)

, òî K(p)

rí

.

rí

Z12 (p)

3.

Имеем: à) Z21(+)(p)

1

, Z21(–)(p)

p

;

2p2

6p

1

á) Z21(+)(p)

3p

, Z21(–)(p)

2p

; â) Z21(+)(p)

8p2

2

1

	Ðèñ. P15.3
0,5p	, Z21(–)(p)	0,5p	,
p2 0,2
		p2 0,5

и с помощью соотношений Z1(p) 2Z21(–)(p), Z2(p) 2Z21(+)(p) находим параметры элементов мостовой схемы (рис. P15.3).

17.1. Расчет установившихся режимов длинной линии

ВОПРОСЫ

1. Время прохождения электромагнитной волны от входных до оконечных зажимов воздушной линии составляет T l/v 10–5 c. В течение этого промежутка времени при условии варианта à приложенное к линии напряжение практиче- ски не меняется, так как период его изменения в 1/fT 2000 раз превышает время T. Поэтому в этом случае воздушную линию можно рассматривать как электрическую цепь с сосредоточенными параметрами.

Однако при условии варианта á период изменения приложенного к линии напряжения, составляющий 10–5 с, оказывается равным промежутку времени T, и воздушную линию следует рассматривать как электрическую цепь с распределенными параметрами.

Длительность действия импульса напряжения (вариант â), равная 3 10–6 c, меньше времени T его прохождения от входных к оконечным зажимам линии, так что в этом случае воздушную линию нельзя рассматривать как электрическую цепь с сосредоточенными параметрами.

УПРАЖНЕНИЯ

2. Учитывая, что À-параметры четырехполюсника, эквивалеíòíого длинной однородной линии, суть À D ch Ξl, из соотношения ch Ρ1 AD (см. § 14.1) находим искомую связь между мерой передачи четырехполюсника и коэффициентом распространения линии: ch Ρ1 ch Ξl, èëè Ρ1 Ξl, 1 l, Π1 Πl.

Ðèñ. P17.2

Ðèñ. P17.1

542 Ответы на вопросы, решения упражнений и задач

3. НапряжениеU 2 è òîê I 2 в точке линии с координатой õ2 можно рассчитать для условий соответствующего варианта с помощью выражений

à) U

U

ch Ξl – I

Z sh Ξl;

I

U1

sh Ξl + I

ch Ξl;

2

2

1

1

Z

1

á) U

U

ch Ξl + I

Z sh Ξl;

I

U 2

sh Ξl + I ch Ξl;

2

1

1

2

Z

1

â) U

U

ch

Ξ l

+ I

Z sh

Ξ l

;

I

U 2

sh

Ξ l

+ I

ch

Ξ l

;

2

1

2

1

2

2

Z

2

1

2

ã) U

U

ch

Ξ l

– I

Z sh

Ξ l

;

I

U1

sh

Ξ l

+ I

ch

Ξ l

;

2

1

2

1

2

2

Z

2

1

2

ä) U

U

ch

Ξ l

+ I

Z sh

Ξ l

;

I

U 2

sh

Ξ l

+ I

ch

Ξ l

;

2

1

2

1

2

2

Z

2

1

2

å) U

U

ch

Ξ l

– I

Z sh

Ξ l

;

I

U 2

sh

Ξ l

+ I

ch

Ξ l

.

2

1

2

1

2

2

Z

2

1

2

6. При условии rC gL волновое сопротивление линии будет активным, при условии gL > rC — индуктивным, а при условии gL < rC — емкостным.

8.Искомая индуктивность равна L (rCl/g) 0,04 Ãí.

9.Напряжение и ток распределены вдоль координаты õ ëè-

нии, отсчитываемой от ее входа, по закону U(x) U1 exp (– x), I(x) I1 exp (– x), где коэффициент затухания равен rg 10 3 êì–1. На рис. P17.1 показана зависимость U(x).

10. Звено цепной схемы, эквивалентное двухпроводной линии, изображено на рис. P17.2.

12. Òàê êàê r g 0, то, используя выражение для скорости распространения

волн вдоль линии v		1		, получаем l v				.
					L	C
		LC			ý		ý

14. 1) Zïð 0; 2) Zïð 0; 3) Zïð ; 4) Zïð 0; 5) Zïð ; 6) Zïð ; 7) Zïð 3 – j; 8) Zïð ; 9) Zïð 2 – j; 10) Zïð 2 + j; 11) Zïð –1 + 2j; 12) Zïð 2 + j.

15. Z5–6 r, Z3–4 r/2, Z1–2 r/3.

17.2. Неискажающая длинная линия

ЗАДАЧИ

1. Требуемый коэффициент усиления k напряжения находим из условия равенства напряжений u1 u2 на входе и выходе линии, связанных соотношением u2 ku1exp (– l ), k exp ( l ) 1,105.