
- •Змістовий модуль 2
- •2. Основні властивості невизначеного інтеграла Враховуючи означення невизначеного інтеграла
- •3. Таблиця найпростіших інтегралів
- •4. Незалежність виду невизначеного інтеграла від вибору аргументу
- •6. Комплексні числа.
- •3. Інтегрування дробів
- •4.Інтегрування найпростіших ірраціональностей
- •5. Підстановки Ейлера
- •6. Інтегрування диференціальних біномів
- •7. Інтегрування тригонометричних функцій
- •Семінарське заняття 11
- •Тема 10. Визначений інтеграл. Невласні інтеграли. Кратні інтеграли
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •Визначений інтеграл. Невласні інтеграли 1-го і 2-го роду
- •1. Визначений інтеграл та його геометрична інтерпретація
- •2. Властивості визначеного інтеграла
- •3. Формула Ньютона-Лейбніца
- •4. Наближене обчислення інтеграла
- •5. Невласні інтеграли першого і другого роду. Поняття про кратні інтеграли
- •Наприклад
- •Наприклад. Інтеграл – абсолютно збіжний інтеграл, оскільки, а– збіжний інтеграл (читачеві рекомендується перевірити це самостійно).
- •6. Застосування визначеного інтегралу
- •Економічні застосування інтегралів
- •Семінарське заняття 12
- •Тема 11. Числові ряди
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •2. Властивості збіжних рядів
- •Дійсно, якщо –– на частинна сума ряду (1), а–– на частинна сума ряду (2), то , і.
- •Якщо ряд (1) збігається, то його – ний член прямує до нуля при необмеженому зростанні.
- •Семінарське заняття 13
- •2. Інтервал і радіус збіжності.
- •3. Властивості степеневих рядів
- •Так, якщо
- •4. Ряди Тейлора і Маклорена. Приклади
- •Підкреслимо, що ряд Тейлора представляє дану функцію тільки тоді, коли(в противному випадку ряд може збігатися до іншої функції). Наведемо кілька важливих рядів Маклорена
- •Ряди по ортогональних функціях
- •Ряди Фур'є Функціональний ряд
- •Розглянемо ряд
- •2. Властивості функціональних рядів
- •Семінарське заняття 14
- •Тема 13. Загальні відомості про диференціальні рівняння. Деякі типи диференціальних рівнянь першого порядку
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •Семінарське заняття 15
- •Тема 14. Диференціальні рівняння вищих порядків
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •Рівняння виду
- •Семінарське заняття 17
- •Семінарське заняття 18
- •Тема 14. Диференціальні рівняння вищих порядків. Лдр вищого порядку з правою частиною спеціального виду
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •9.1. Основні поняття
2. Основні властивості невизначеного інтеграла Враховуючи означення невизначеного інтеграла
![]()
можна легко довести основні його властивості
Диференціал невизначеного інтеграла дорівнює підінтегральному виразу, а похідна – підінтегральній функції:
![]()
![]()
Невизначений інтеграл від диференціала неперервно диференційованої функції дорівнює самій цій функції з точністю до сталого доданка:
![]()
Зауважимо,
що в підкреслених виразах знаки
![]() і
і![]() взаємно
знищують один одного. У цьому розумінні,
як вже згадувалося, диференціювання та
інтегрування євзаємно
оберненими
математичними операціями.
взаємно
знищують один одного. У цьому розумінні,
як вже згадувалося, диференціювання та
інтегрування євзаємно
оберненими
математичними операціями.
Відмінний від нуля сталий множник можна виносити за знак невизначеного інтеграла:
![]()
Дійсно:
![]()
![]() .
.
При
цьому
![]() – первісна для
– первісна для![]() оскільки
оскільки![]()
Невизначений інтеграл від алгебраїчної суми скінченого числа неперервних функцій дорівнює такій же алгебраїчній сумі невизначених інтегралів цих функцій.
Нехай,
наприклад,
![]() – неперервні функції в проміжку
– неперервні функції в проміжку![]() .
Тоді має місце рівність:
.
Тоді має місце рівність:
![]()
![]() .
.
Дійсно:
![]()
![]()
![]() Функція
Функція
![]() – первісна для функції
– первісна для функції![]() ,
оскільки
,
оскільки![]() .
Отже,
.
Отже,
![]()
3. Таблиця найпростіших інтегралів
Безпосереднім диференціюванням перевіряється справедливість наступних табличних формул.

 .
.
 .
.

 .
.








 .
.



4. Незалежність виду невизначеного інтеграла від вибору аргументу
Має
місце незалежність невизначеного
інтеграла від вибору аргументу, так що
таблиця інтегралів вірна не тільки
тоді, коли
![]() – незалежна змінна, але і у випадку,
коли замість
– незалежна змінна, але і у випадку,
коли замість![]() фігурує неперервно диференційована
функція
фігурує неперервно диференційована
функція![]() .
Таким чином, якщо
.
Таким чином, якщо![]() то
то![]() що перевіряється безпосереднім
диференціюванням.
що перевіряється безпосереднім
диференціюванням.
На підставі цієї властивості одержується узагальнена таблиця найпростіших інтегралів, в якій, скажімо, перша формула має вигляд
1.
![]()
![]()
де
![]() – будь-яка неперервно диференційована
функція від незалежної змінної.
– будь-яка неперервно диференційована
функція від незалежної змінної.
Наприклад.
№1.
![]()
Тут
![]() і ми користуємося “табличною” формулою
і ми користуємося “табличною” формулою![]()
№2.
![]()
Відзначимо такі корисні для інтегрування властивості диференціала
|
|
|
|
|
|
|
|
|
Наведемо ще деякі приклади.
№3
![]() .
.
№4
![]()
№5.
![]() .
.
№6

№7.
![]()
5. Інтегрування методом заміни змінної (способом підстановки) та по частинах
Існує два основних методи інтегрування – метод заміни змінних (спосіб підстановки) а) та метод інтегрування по частинах б).
а)
Нехай потрібно знайти
![]() який не є табличним інтегралом (але
відомо, що існує). Виконаємо в
підінтегральному виразі заміну:
який не є табличним інтегралом (але
відомо, що існує). Виконаємо в
підінтегральному виразі заміну:![]() (тут
(тут![]() та
та![]() – неперервні функції, причому існує
обернена функція
– неперервні функції, причому існує
обернена функція![]() ).
).
Доведемо, що
![]()
Для цього покажемо, що похідні зліва і справа рівні між собою.
Похідна
зліва:
![]()
Похідна
справа:
![]()
Формула
доведена. Зауважимо, що функція
![]() може бути задана неявно і що замість
може бути задана неявно і що замість![]() ,
звичайно, можна використовувати іншу
букву –
,
звичайно, можна використовувати іншу
букву –![]() і т.п.
і т.п.
Наприклад.
№1.
![]()
№2.

б)
Нехай
![]()
![]() – неперервно диференційовані функції.
Тоді, як відомо,
– неперервно диференційовані функції.
Тоді, як відомо,![]() або
або![]() Інтегруючи цю рівність, одержуємо:
Інтегруючи цю рівність, одержуємо:
![]()
Ми
одержали формулу
інтегрування по частинах:
![]()
Наприклад.
№1.
![]()
№2.

Зауважимо,
що як правило, функції
![]() та
та![]() входять до складу функції
входять до складу функції![]() при інтегруванні по частинах.
при інтегруванні по частинах.
6. Комплексні числа.
Комплексне
число – це вираз виду а+ві,
де а,
в – дійсні
числа, а і
– уявна
одиниця (і=![]() ).
Наприклад, квадратне рівняння х2-2х+2=0
не має дійсних коренів, але має пару
комплексно спряжених коренів: 1+і;
1-і.
Крім алгебраїчної форми запису
комплексного числа а+ві,
часто користуються тригонометричною
формою. З геометричної точки зору,
комплексному числу а+ві
відповідає точка площини, абсциса якої
–а,
а
ордината – в.
).
Наприклад, квадратне рівняння х2-2х+2=0
не має дійсних коренів, але має пару
комплексно спряжених коренів: 1+і;
1-і.
Крім алгебраїчної форми запису
комплексного числа а+ві,
часто користуються тригонометричною
формою. З геометричної точки зору,
комплексному числу а+ві
відповідає точка площини, абсциса якої
–а,
а
ордината – в.
Семінарське заняття 10
Тема 9. Інтегрування раціональних та ірраціональних виразів
Питання для усного опитування та дискусії
9.5 . Найпростіші дроби та їх інтегрування.
9.6. Інтегрування правильних і неправильних раціональних дробів.
9.7. Інтегрування найпростіших ірраціональних виразів.
9.8. Підстановки Ейлера. Диференціальний біном.
9.9. Інтегрування тригонометричних функцій.
Аудиторна письмова робота
Виконання студентами тестових завдань з питань теми заняття.
Методичні вказівки
Ключовими термінами, на розумінні яких базується засвоєння навчального матеріалу теми, є : найпростіші (елементарні) дроби 1-го, 2-го, 3-го, 4-го типу, правильний раціональний дріб, неправильний раціональний дріб, найпростіші ірраціональності, три випадки інтегровності диференціального бінома, універсальна тригонометрична підстановка.
З метою глибокого засвоєння навчального матеріалу при самостійному вивченні теми студенту варто особливу увагу зосередити на таких аспектах.
1.Інтегрування раціональних дробів
Розкладання многочленів на множники.
Нагадуємо,
що функція
![]() де
де![]() – ціле додатне число, називаєтьсямногочленом
(поліномом)
або цілою
раціональною функцією від х.
Число
– ціле додатне число, називаєтьсямногочленом
(поліномом)
або цілою
раціональною функцією від х.
Число
![]() називається степенем многочлена. При
цьому
називається степенем многочлена. При
цьому![]() – дійсні або комплексні сталі числа,
– дійсні або комплексні сталі числа,![]() – дійсна або комплексна змінна.
– дійсна або комплексна змінна.
Рівняння
виду
![]() де
де![]() – многочлен
– многочлен![]() - го степеня, називаєтьсяалгебраїчним
рівнянням
- го степеня, називаєтьсяалгебраїчним
рівнянням
![]() -го степеня.
-го степеня.
Основна
теорема алгебри стверджує, що всяке
алгебраїчне рівняння степеня
![]() >0 має хоча б один корінь, дійсний або
комплексний.
>0 має хоча б один корінь, дійсний або
комплексний.
Представимо
![]() у вигляді
у вигляді
![]()
(тут
![]() многочлен, а
многочлен, а![]() – залишок від ділення
– залишок від ділення![]() на
на![]() ).
При
).
При![]() виконується умова:
виконується умова:![]() Таким чином, залишок від ділення
многочлена
Таким чином, залишок від ділення
многочлена![]() на двочлен
на двочлен![]() при
при![]() дорівнює значенню цього многочлена
дорівнює значенню цього многочлена![]() (теорема Безу).
(теорема Безу).
Якщо
![]() тобто
тобто![]() є коренем многочлена, то
є коренем многочлена, то![]() і
і![]() Тут
Тут![]() – многочлен степеня
– многочлен степеня![]() старший коефіцієнт якого дорівнює
старший коефіцієнт якого дорівнює![]() .
Якщо цей многочлен не є тотожно сталою,
то до нього можна знову застосувати
основну теорему алгебри. Якщо
.
Якщо цей многочлен не є тотожно сталою,
то до нього можна знову застосувати
основну теорему алгебри. Якщо![]() – корінь рівняння
– корінь рівняння![]() то
то![]() Продовжуючи цей процес, одержуємо:
Продовжуючи цей процес, одержуємо:![]() Якщо кратність кореня
Якщо кратність кореня![]() кореня
кореня![]() кореня
кореня![]() то
то![]()
![]()
Отже,
алгебраїчне рівняння
![]() - го степеня має
- го степеня має![]() коренів (якщо кожен корінь рахувати
стільки разів, яка його кратність).
коренів (якщо кожен корінь рахувати
стільки разів, яка його кратність).
Якщо
коефіцієнти многочлена
![]() – дійсні числа і комплексне число
– дійсні числа і комплексне число![]() є коренем многочлена
є коренем многочлена![]() ,
то спряжене йому, число
,
то спряжене йому, число![]() також є коренем многочлена. Зауважимо,
що зручно об’єднувати співмножники
виду
також є коренем многочлена. Зауважимо,
що зручно об’єднувати співмножники
виду
![]()
![]() .
Таким чином, многочлен
.
Таким чином, многочлен
![]() можна розкласти на лінійні та квадратичні
співмножники:
можна розкласти на лінійні та квадратичні
співмножники:
![]()
Якщо
два многочлена рівні один одному при
будь-яких значеннях
![]() ,
то рівня їх степені та рівні між собою
коефіцієнти при однакових степенях:
якщо
,
то рівня їх степені та рівні між собою
коефіцієнти при однакових степенях:
якщо
![]() ,
,
то
![]()
Зауваження.
Для випадків, коли
![]() рівняння
рівняння![]() розв’язуються за формулами, відомими
з шкільного курсу математики. При
розв’язуються за формулами, відомими
з шкільного курсу математики. При![]() та
та![]() також існують загальні формули
розв’язування таких рівнянь – формули
Кардано і Феррарі. Доведено, що при
також існують загальні формули
розв’язування таких рівнянь – формули
Кардано і Феррарі. Доведено, що при![]() не існує формул для розв’язування
рівнянь
не існує формул для розв’язування
рівнянь![]() в радикалах.
в радикалах.
Розкладання раціональних дробів на найпростіші
Нехай
многочлени
![]() та
та![]() не мають спільних коренів.Раціональним
дробом
називається відношення двох многочленів
не мають спільних коренів.Раціональним
дробом
називається відношення двох многочленів
![]()
Якщо
степінь чисельника менше степені
знаменника, тобто
![]() то дріб називаєтьсяправильним,
якщо ж
то дріб називаєтьсяправильним,
якщо ж
![]() – неправильним.
– неправильним.
У
випадку неправильного дробу чисельник
ділять на знаменник та представляють
даний дріб у вигляді суми многочлена
та деякого правильного дробу:
![]()
Після
цього правильний нескоротний дріб
![]() розкладають на найпростіші раціональні
дроби.
розкладають на найпростіші раціональні
дроби.
Правильні раціональні дроби виду

 (
( ціле число);
ціле число);


 називається
найпростішими
дробами І, ІІ, ІІІ, ІV
типів.
називається
найпростішими
дробами І, ІІ, ІІІ, ІV
типів.
Має місце
Теорема
1.
Нехай
![]() корінь знаменника кратності
корінь знаменника кратності![]() ,
тобто
,
тобто![]() де
де![]()
Тоді
даний правильний нескоротний дріб
![]() можна представити у вигляді суми двох
інших правильних дробів в такий спосіб:
можна представити у вигляді суми двох
інших правильних дробів в такий спосіб:
![]()
де
![]() – відмінне від нуля стале число, а
– відмінне від нуля стале число, а![]() – многочлен, степінь якого менше степеня
знаменника
– многочлен, степінь якого менше степеня
знаменника![]() .
.
Для
доведення теореми 1 представимо дріб

Підберемо
А так, щоб різниця
![]() ділилася на
ділилася на![]() Згідно з теоремою Безу, для цього
необхідно і достатньо, щоб виконувалась
умова
Згідно з теоремою Безу, для цього
необхідно і достатньо, щоб виконувалась
умова
![]()
Звідси
визначаємо:
![]() Значить, саме при такому значенні А
будемо мати:
Значить, саме при такому значенні А
будемо мати:![]() .
Це і доводить теорему 1.
.
Це і доводить теорему 1.
Цю
ж саму теорему 1 можна застосувати до
виразу
![]() .
Оскільки
.
Оскільки![]() – корінь кратності
– корінь кратності![]() ,
одержимо:
,
одержимо:
![]() де
де
![]() – правильний нескоротний дріб. Має
місце
– правильний нескоротний дріб. Має
місце
![]() Теорема
2.
Якщо
Теорема
2.
Якщо
![]() причому
причому![]() не ділиться на
не ділиться на![]() то правильний раціональний дріб
то правильний раціональний дріб![]() можна представити у вигляді суми двох
інших правильних дробів у такий спосіб:
можна представити у вигляді суми двох
інших правильних дробів у такий спосіб:
![]()
де
![]() – многочлен, степінь якого менше степеня
многочлена
– многочлен, степінь якого менше степеня
многочлена![]() ,
а
,
а![]() і
і![]() – сталі.
– сталі.
Із теореми 1 і 2 випливає такий важливий для практичних застосувань
Висновок.
Якщо
![]() то дріб
то дріб![]() можна представити у вигляді
можна представити у вигляді

Для визначення невизначених коефіцієнтів вираз справа зводять до спільного знаменника, після чого (в чисельниках) прирівнюють коефіцієнти при однакових степенях х зліва і справа. Одержується система для визначення невідомих сталих.
Наприклад.
Представити дріб
![]() у вигляді суми найпростіших дробів.
у вигляді суми найпростіших дробів.
Розв’язування. Згідно з висновком з теорем 1 і 2, маємо:
 .
.
Звідси одержуємо:
![]()
Прирівнюємо
коефіцієнти при
![]() та вільні члени зліва і справа одержуємо:
та вільні члени зліва і справа одержуємо:
 .
.
Розв’язавши систему, маємо:
![]()
Таким
чином,
![]()
Зауваження.
Для того, щоб одержати систему для
визначення
![]() можна скористатися методом коллокації,
який полягає в тому, який полягає в тому,
що рівняння
можна скористатися методом коллокації,
який полягає в тому, який полягає в тому,
що рівняння
![]()
розписують
при чотирьох (по кількості невідомих
фіксованих) значеннях змінної х
(наприклад, при
![]() ):
):
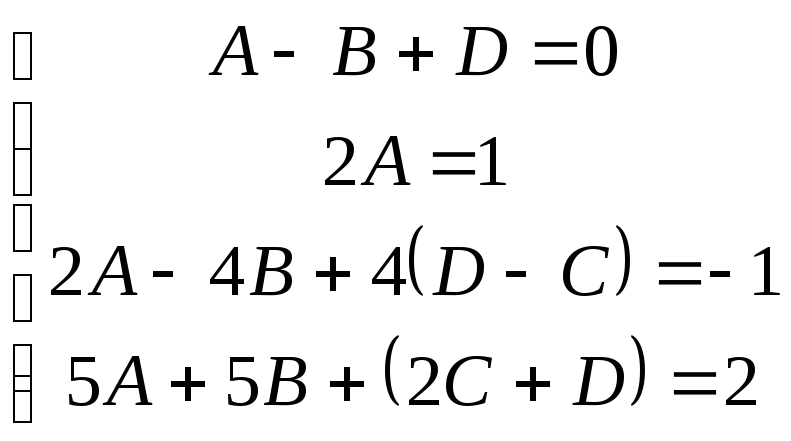 .
.
Розвязуючм систему, одержуємо такий самий розв'язок, як і раніше.
