Наприклад

1. Інтеграл збігається, оскількиа

2. Інтеграл розбігається, оскількипричомуяк було показано вище, розбігається.

На практиці користуються наслідком з цієї теореми – граничною теоремою порівняння, яка формулюється так.

Нехай іта існує границя. Тоді із збіжності інтегралупривипливає збіжність інтегралу, а із розбіжностіпривипливає розбіжність інтегралу.

Таким чином, при обидва інтеграли є або збіжними, або розбіжними.

Нехай – знакозмінна функція.

Можна довести, що із збіжності інтегралу випливає збіжність інтегралу(обернене твердження, взагалі кажучи, невірне). Якщо збігається не тільки інтеграл, але і інтеграл, тоназиваютьабсолютно збіжним, а функцію –абсолютно інтегрованою.

Наприклад. Інтеграл – абсолютно збіжний інтеграл, оскільки, а– збіжний інтеграл (читачеві рекомендується перевірити це самостійно).

ІІ. Узагальнимо поняття визначеного інтегралу на випадок розривної підінтегральної функції.

Припустимо, що функція визначена і неперервна при, а приця функція або не визначена, або терпить розрив. У цьому випадку не можна визначити інтеграл як границю інтегральної суми. За означенням, покладають:

(рис.2).

Якщо границя, що стоїть справа, існує, то інтеграл називається невласним збіжним інтегралом другого роду (в противному випадку – розбіжним).

⁰

Рис. 2. Невласний інтеграл другого роду.

Якщо функція розривна при, то, згідно з означенням,.

У випадку, коли функція розривна всередині відрізка, при, то, якщо обидва інтеграли справа існують.

Наприклад. (інтеграл розбіжний).

У випадку невласного інтегралу другого роду від додатної функції для його збіжності необхідно та достатньо, щоб при всіхвиконувалася нерівність:.

Для невласного інтегралу 2-го роду має місце теорема порівняння, аналогічна сформульованій вище для невласних інтегралів 1-го роду, а також твердження про збіжність інтегралу від знакозмінної функції при умові збіжності інтегралу.

Кратні інтеграли. Подвійні і потрійні інтеграли – це узагальнення поняття визначеного інтегралу на інтеграл по плоскій області (частині площини) та на інтеграл по об’ємній замкненій області. Обчислення подвійних інтегралів зводиться до двохкратного інтегрування, а потрійних – до трьохкратного інтегрування. При вивченні теми «Кратні інтеграли» слід звернути особливу увагу на поняття правильної двохвимірної (та правильної трьохвимірної) областей, на порядок розстановки меж інтегрування, на правила заміни змінних при інтегруванні.

6. Застосування визначеного інтегралу

1. Обчислення площі

Як зазначалося раніше, за допомогою визначеного інтеграла можна знаходити площу криволінійної трапеції, обмеженої неперервною при функцією(при), прямими,та віссю. Якщо, то, і(рис. 1).

0

Рис. 3. Площа .

Якщо – знакозмінна функція при, то. Для знаходження площі у випадку, представленому на рис. 4, користуються формулою:.

₀

Рис. 4. Площа .

Якщо крива задана в параметричній формі , де, причому,, то, виконавши у формулізаміну, одержимо

(при цьому припускається, що та) – неперервні функції при.

Наприклад. Знайти за допомогою інтеграла площу чверті круга (рис. 5).

1

х

Рис.5. Чверть круга .

Розв'язування. Параметричні рівняння кола мають вигляд: . Площа чверті круга, розміщеного в першій координатній чверті, визначається за формулою:

.

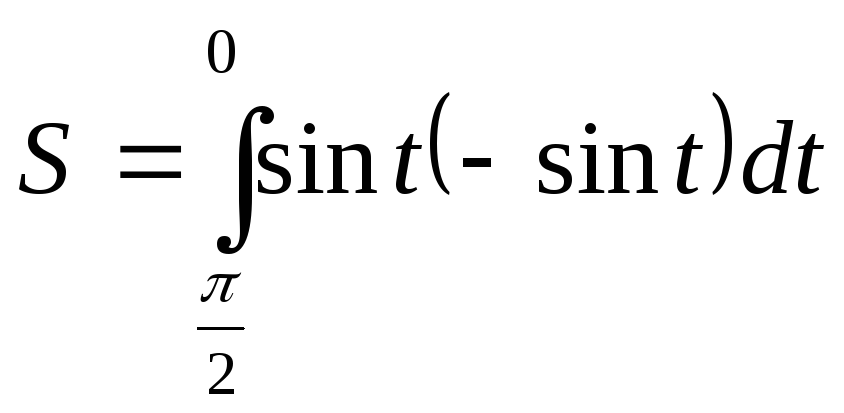Виконавши обчислення, одержимо:

(кв. од.)

Зауважимо, що цю площу можна знайти за допомогою інтеграла .

Розглянемо питання про визначення площі криволінійного сектора в полярних координат (рис.6).

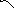
Рис. 6. Криволінійний сектор ОАВ.

Нехай – неперервна функція при. Криволінійний сектор ОАВ обмежений променямита. Щоб знайти його площу, скористаємося основною ідеєю інтегрального числення: розіб’ємо дану площу начастин. На участкувибираємота обчислюємо.

Апроксимуємо -тий участок розбиття круговим сектором з радіусомта центральним кутом . Його площа . Складемо інтегральну сумута перейдемо до її границі при. З одного боку, при цьому одержуємо площу криволінійного сектора, а з іншого – визначений інтеграл.

Наприклад, площа фігури, утвореної одним витком спіралі Архімеда при(рис. 7), дорівнює:(кв. од.).

0

Р

Рис. 7 Виток спіралі Архімеда при

2. Знаходження довжини дуги

Важливим геометричним застосуванням визначеного інтеграла є знаходження довжини дуги кривої лінії:

Нехай крива задана рівнянням . Знайдемо довжину дуги(рис. 8).

Рис. 8. Дуга кривої.

Що ж таке довжина дуги? Щоб дати означення цього поняття, виберемо на дузі точки та з’єднаємо їх хордами. Довжини цих хорд позначимо відповідно. довжина ламаної, вписаної в такий спосіб, дорівнює:.

Довжиною дуги називається границя, до якої прямує довжина вписаної ламаної, коли довжина її найбільшої ланки прямує до нуля: .

Нехай та– неперервні функції при. Очевидно,. Використовуючи теорему Лагранжа маємо:де.

Отже, , а. Перейшовши до границі приодержимо:.

Якщо ж крива задана параметричними рівняннями , причому, то в останньому інтегралі слід виконати підстановку. Нехай. Одержуємо: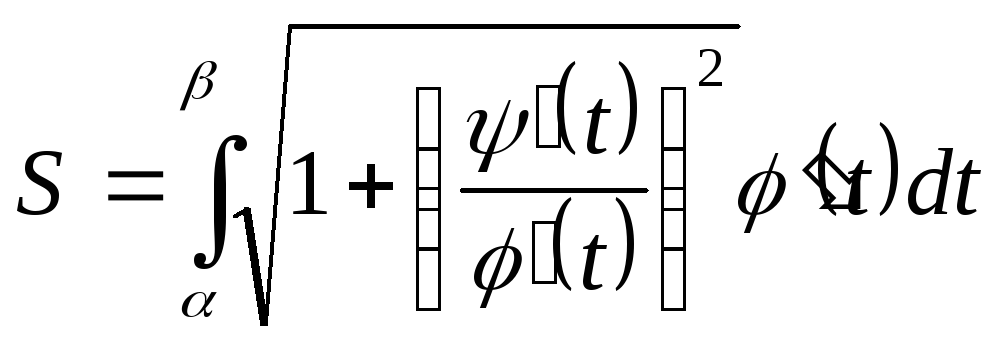, або остаточно

Можна довести, що для просторової кривої, заданої параметричними рівняннями , має місце аналогічна формула

(якщо та– неперервні функції).

Якщо лінія задана в полярній системі координат рівнянням , то, враховуючи формулу переходу від полярних до декартових координат, одержуємо параметричні рівняння кривої. Оскількимаємо:і.

Наприклад. Знайти довжину дуги кардіоїди .

Розв'язування. Побудуємо графік цієї кривої в полярній системі координат (рис. 7).

0 Р

Рис. 9. Кардіоїда

Враховуючи симетричність графіка відносно полярної осі, а також те, що , маємо:

.

3. Об’єм тіла обертання

За допомогою інтегралу можна знайти об’єм тіла, якщо відомі площі його паралельних перерізів.

Нехай відома площа будь-якого перерізу даного тіла площиною, перпендикулярною до осі(рис. 10).

0

Рис. 10. Об’єм тіла V

Припустимо, що – неперервна функція від. Проведемо площини через точкита виберемо точкув кожному з проміжків. Об’ємприблизно дорівнює об’єму циліндра, твірна якого паралельна осі, а направляюча – це контур перетину тіла площиною. Об’єм такого елементарного циліндрадорівнює. Сума об’ємів таких елементарних циліндрів– це інтегральна сума для неперервної функції. Перейшовши до границі при, одержимо формулу для знаходження об’єму тіла:

.

Площа перерізу , зокрема відома для тіла обертання, утвореного обертанням навколо осінеперервної кривої. (рис. 9).

Рис. 11. тіло обертання навколо осі

Будь-який переріз цього тіла – це круг радіуса . площа такого перерізу, отже, об’єм тіла, згідно з доведеною формулою, визначається так:

.