Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки

Ключовими термінами, на розумінні яких базується засвоєння навчального матеріалу теми, є : інтегральна сума, визначений інтеграл, геометрична інтерпретація визначеного інтеграла, заміна змінних у визначеному інтегралі, інтегрування по частинах у визначеному інтегралі, невласні інтеграли першого роду, невласні інтеграли другого роду, подвійні інтеграли, правильна область (в напрямку осі Ох, осі Оу), двохкратні інтеграли, потрійні інтеграли, трьохкратні інтеграли, обчислення площ, об’ємів, довжини дуги за допомогою інтегралів.

З метою глибокого засвоєння навчального матеріалу при самостійному вивченні теми студенту варто особливу увагу зосередити на таких аспектах:

Визначений інтеграл. Невласні інтеграли 1-го і 2-го роду

1. Визначений інтеграл та його геометрична інтерпретація

Нехай функція неперервна на проміжку:. Нехайі– найменше та найбільше її значення на цьому відрізку. Відрізокрозіб’ємо начастин точкамита позначимо:

Найменше та найбільше значення функції на відрізкувідповідно позначимота. Складемо дві суми:

та

.

Ці суми називаються відповідно нижньою і верхньою сумами Дарбу.

Відзначимо такі властивості нижніх і верхніх інтегральних сум.

оскільки при всіх .

Введемо поняття про інтегральну суму для функції . Візьмемо в кожному відрізкуточкутак, що. Обчислимо значення функції в цих точках та складемо суму

Це – інтегральна сума для функції . Яке б не було ,так щоі, значить,Сумазалежить від способу розбиття проміжкуна відрізкита від вибору точок. Неважко уявити собі розбиття проміжкуна елементарні участкиза допомогою більшого числа точок, причому такого, щоб величинапри цьому зменшилася. Нехайта.

Якщо при будь-якому діленні відрізка такому, щоі при довільному виборі точоксумапрямує до однієї й тієї ж самої границі, то говорять, що функціяінтегрована на відрізку, а границюназиваютьвизначеним інтегралом від на і позначають :

Число називають нижньою межею інтеграла,– його верхньою межею. Проміжокназивають відрізком інтегрування, а– змінною інтегрування.

Можна довести, що коли функція неперервна на проміжку, то вона на цьому проміжку інтегрована.

Геометричний зміст визначеного інтеграла стає зрозумілим, коли зауважити, що

,

Нехай . Інтегралчисельно дорівнює площі криволінійної трапеції, обмеженої кривоюта прямимиі віссю.

За означенням приймається, що коли тоі що.

2. Властивості визначеного інтеграла

Визначений інтеграл має властивості, які можна сформулювати за допомогою знаків рівностей або нерівностей.

1. Сталий множник можна виносити за знак інтеграла:

Дійсно,

2) Визначений інтеграл від алгебраїчної суми кількох функцій дорівнює алгебраїчній сумі інтегралів від доданків.

Це дійсно так, оскільки (Властивості 1) і 2) вірні і при , і при.)

2. Якщо при, то.

Це дійсно так, оскільки

. Значить, , що і потрібно було довести.

4. Якщо і– найменше і найбільше значення функції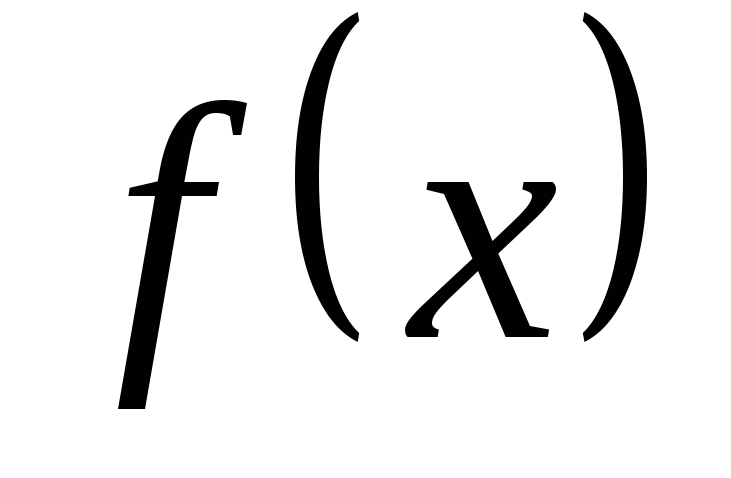при, то

.

Ця властивість випливає з попередньої, якщо врахувати, що і що, а.

4. Якщо функція неперервна на проміжку, то існує таке число

, що . (Цю властивість називають теоремою про середнє).

Дійсно, нехай . За попередньою властивістю одержуємо:

, або , де. Оскільки функціянеперервна на, вона приймає на цьому проміжку всі свої проміжні значення міжі. Отже, існує таке значення, при якому, тобто.

4. Для будь-яких трьох чисел має місце рівність:

(якщо всі три інтеграла існують).

Дійсно, якщо, скажімо, то, складаючи інтегральну суму для функціїна, вибираємо точкуоднією з точок поділу. Маємо:

.

Перейдемо до границі при і одержуємо потрібну властивість, якщо ж, то, або

.

Аналогічно розглядаються інші способи взаємного розміщення точок і.