Типові задачі і їх розв’язуваня

1. Складові тадискретної випадкової величини, яка задана своїм законом розподілу (див. табл. 1), характеризують якість виробленої продукції. Визначити безумовні закони розподілу випадкових величинтаі обчислити

Таблиця 1

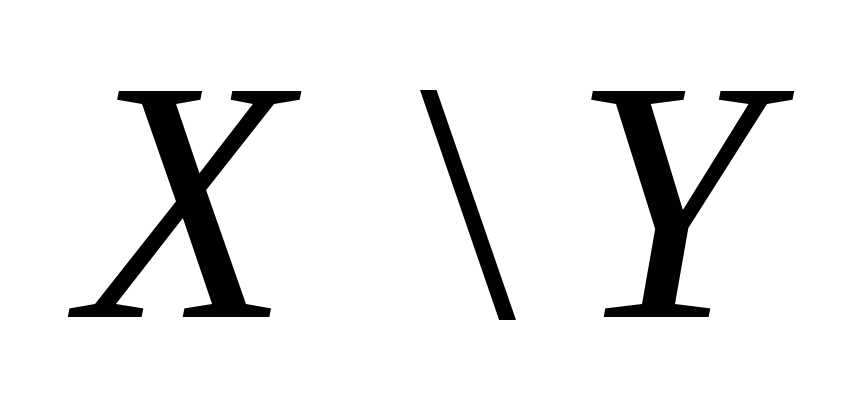
	-2	0	1	2
0	0,15	0,1	0,05	0
1	0	0,2	0,1	0,1
2	0,05	0	0,15	0,1

Розв’язування. Для визначення закону розподілу випадкової величини використаємо із (4) першу формулу

Тобто, Отже, закон розподілу випадкової величинимає вигляд

Таблиця 2

	0	1	2
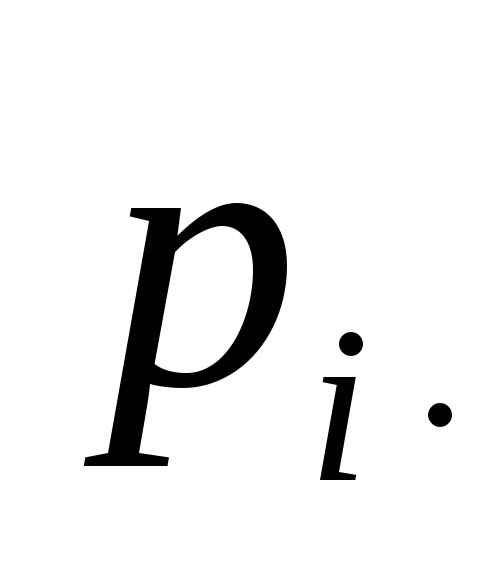
	0,3	0,4	0,3

Аналогічно за формулою

будемо мати Ураховуючи ці значення, закон розподілу випадкової величинибуде мати вигляд

Таблиця 3

	-2	0	1	2
	0,2	0,3	0,3	0,2

Для обчислення дисперсій випадкових величин тавирахуємо спочатку їхні початкові моменти першого та другого порядку, тобто,В результаті одержимо

Звідси

2. За законом розподілу дискретної двовимірної випадкової величини

Таблиця 4

	1	2	4	5
-1	0,1	0,15	0	0,05
1	0	0,25	0,15	0,1
3	0	0	0,15	0,05

вивести умовний закон розподілу випадкової величини за умови, що, умовний закон розподілу випадкової величиниза умови, що, знайти умовні математичні сподіванняі

Розв’язування. Знайдемо умовні ймовірності випадкової величини за формулою (5)

де . Оскількито

Отже, умовний закон розподілу випадкової величини за умови, що випадкова величинанабуде значення, має вигляд

Таблиця 5

	-1	1	3
	0,25	0,5	0,25

Аналогічно, використовуючи формулу (6), знайдемо умовний закон розподілу випадкової величини за умови, що. Оскількито

Тому, умовний закон розподілу випадкової величини за умови, що випадкова величинанабуде значення, буде мати вигляд

Таблиця 6

	1	2	4	5
	0	0,5	0,3	0,2

Тепер знайдемо шукані умовні математичні сподівання. При цьому урахуємо, що вони розраховуються за формулами (7), (8).

3. За заданою функцією розподілу

неперервної двовимірної випадкової величини знайти ймовірність попадання випадкової точкив прямокутник, обмежений прямими

Розв’язування. Ймовірність того, що випадкова точка попаде у прямокутник , можна обчислити за формулою (2)

або за другою властивістю двовимірної щільністю розподілу.

Скориставшись цією формулою, одержимо

4. Неперервна двовимірна випадкова величина задана своєю щільністю розподілу

.

Обчислити постійну С.

Розв’язування. Скористаємось третьою властивістю двовимірної щільністю розподілу

 

В результаті одержимо

 

5. Знайти математичні сподівання складових танеперервної двовимірної випадкової величини, якщо задана щільність її розподілу

Розв’язування. Для знаходження математичного сподівання неперервної випадкової величини потрібно знати її щільність розподілу. Оскільки нам задана щільність розподілу двовимірної випадкової величини, то використаємо для цього формулу (10). Отже,

Враховуючи, що

одержимо

Тепер знайдемо математичне сподівання складової :

Отриманий інтеграл будемо знаходити за частинами. Нехай , аЗвідсиаТоді

Урахувавши, що інтеграл Пуассона , одержимо

Аналогічно одержимо

і

6. Знайти коефіцієнт кореляції компонент двовимірного випадкового величини , заданого своїм законом розподілу (див. табл. 7).

Таблиця 7

	-1	2	3
1	0,15	0,05	0,1
4	0,25	0,15	0,3

Розв’язування. Щоб обчислити коефіцієнт кореляції, потрібно знати величину коваріації випадкового вектора та середні квадратичні відхилення його складових (див формулу (24)). Тому спочатку знайдемо закони розподілу складовихта. Вони будуть мати вигляд (див розв’язування задачі 1):

Таблиця 8

	-1	2	3
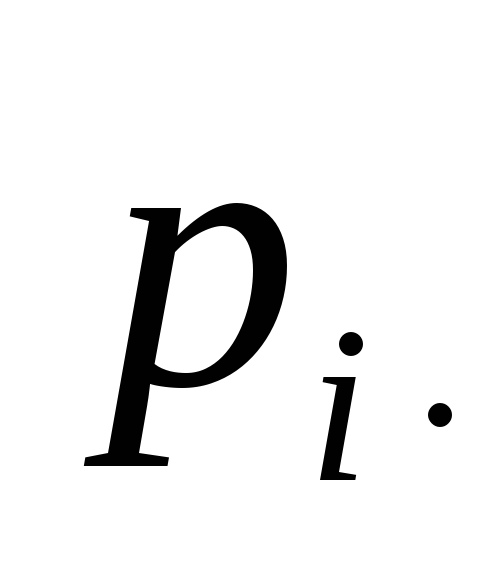
	0,4	0,2	0,4

Таблиця 9

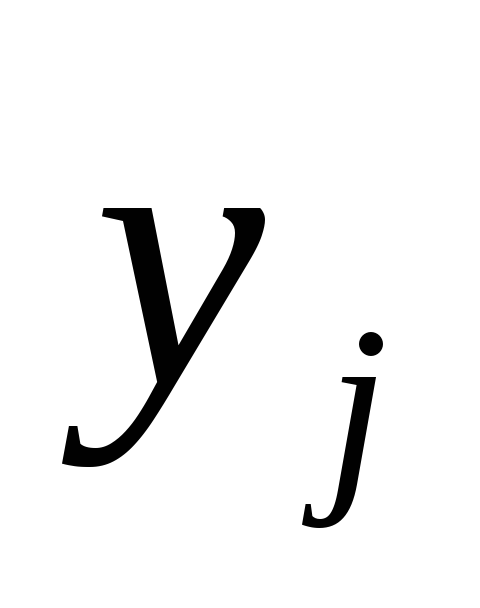
	1	4
	0,3	0,7

Тепер розрахуємо середні квадратичні відхилення випадкових величин та.

Коваріацію випадкової величини знайдемо за формулою (22)

Розрахуємо початковий момент (1+1) порядку.

Тобто

Звідси

Остаточно одержимо