5. Послідовність незалежних випробувань. Формула Бернуллі Теоретичні положення

До сих пір в основному ми розглядали випадки коли проводилося одне чи декілька випробувань. Однак, на практиці часто проводиться не одне, а серія випробувань. Одним з найпростіших є той випадок, коли всі ці випробування незалежні між собою і в кожному з цих випробувань може відбутися подія А з однаковою ймовірністю р.

Наприклад, ми підкидаємо одну і ту ж монету сто раз. Зрозуміло, що при кожному підкиданні цієї монети на верхній її поверхні після того, як вона впаде може випасти або цифра, або герб. Ймовірність випадання цифри дорівнює 0,5. Однак реально при таких ста підкиданнях цієї монети на верхній її поверхні цифра може не випасти ні одного разу, випасти один, два і т.д. аж до сто разів. Виникає питання – яка ймовірність того, що на верхній поверхні цієї монети цифра випаде якусь задану кількість разів ? Знайти цю ймовірність можна за допомогою формул Бернуллі чи їх модифікацій.

Нехай виконують скінченну кількість п послідовних випробувань. Якщо наслідки цих випробувань незалежні, то ці випробування називаються незалежними. Припустимо, що у кожному з п незалежних випробувань подія А може відбутися з однаковою ймовірністю р і не відбутися з ймовірністю . Тоді можна знайти ймовірність того, що в цих випробуваннях подіяА може з’явитися рівно разів.

Ймовірність того, що в серії з послідовних незалежних випробувань подіяможе з’явитисяразів, за умови, що в кожному випробуванні подіяз’являється з ймовірністюі не з’являється з ймовірністю, обчислюється за формулою

. (1)

Розглянута схема і формула (1) названі ім’ям Я. Бернуллі.

Формулу Бернуллі (1) можна довести таким чином. Ймовірність однієї складеної події, яка полягає у тому, що в випробуваннях подія настане раз і не настане раз, за теоремою про добуток ймовірностей незалежних подій, дорівнює.

У зв’язку з цим, що ці складені події несумісні, за теоремою додавання ймовірностей несумісних подій шукана ймовірність дорівнює сумі ймовірностей всіх можливих складених подій. Оскільки ймовірність всіх складених подій однакова, то шукана ймовірність (настання раз події в випробуваннях) дорівнює ймовірності однієї складеної події , помноженій на їхню кількість. А ця кількість дорівнює кількості комбінацій ізелементів поелементів, тобто. Таким чином, ми вивели формулу

,

що і треба було довести.

На підставі формули Бернуллі (1) можна отримати і такі формули, які часто використовуються на практиці.

Ймовірність того, що в п незалежних випробувань подія А може відбутися не менше, ніж і не більше, ніжразів, можна обчислити за формулою

(2)

Формулу (2) можна використати, зокрема, для випадку, коли нам потрібно знайти Ймовірність того, що в п незалежних випробувань подія А може відбутися менше разів (), не більшеразів (), більшеразів () і не меншеразів().

Ймовірність того, що в п незалежних випробувань подія А відбудеться хоча б один раз, обчислюють за формулою

(3)

З логічних міркувань зрозуміло, що при підкиданні монети сто раз найбільша ймовірність появитися цифрі на верхній поверхні цієї монети досягається для числа 50. У багатьох випадках треба знайти найбільш ймовірне значення числапояв події.

Число для якого ймовірністьє найбільшою називаютьнайімовірнішим числом настання подій (найбільшою частотою, модою).

Найімовірніше число настання події в схемі Бернуллі є в інтервалі

(4)

Для того, щоб можна було застосувати схему Бернуллі до розв’язування задач, потрібно, щоб виконувались такі умови: 1) випробування, які виконують повинні бути незалежними; 2) кожне випробування повинно мати два результати; 3) ймовірність появи заданої події повинна бути однаковою у кожному випробуванні.

Обчислення ймовірностей за формулами (1), (2) при досить великих та при малихабоускладнюється. Вони стають громіздкими та можуть мати значні похибки за рахунок заокруглень у деяких множниках. У таких випадках замість формули Бернуллі часто можна використовувати наближені асимптотичні формули.

Вкажемо наслідки із граничних теорем, які містять наближені формули для ймовірностей

,

Наслідок 1 (з локальної теореми Мавра-Лапласа). Якщо у схемі Бернуллі кількість випробувань достатньо велика, а ймовірністьпояви подіїв усіх випробуваннях однакова, то ймовірністьпояви подіїразів може бути знайдена залокальною формулою Мавра-Лапласа

(5)

де

(6)

Функцію часом називають локальною функцією Лапласа. Вона має такі властивості:

1. функція визначена для усіх ;

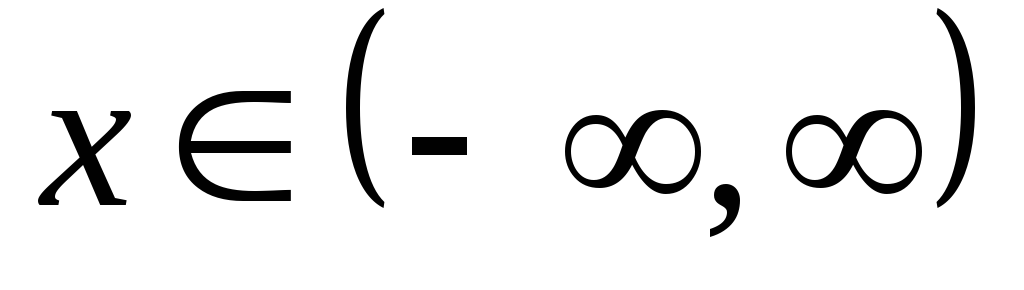2. функція є парною, тобто ;

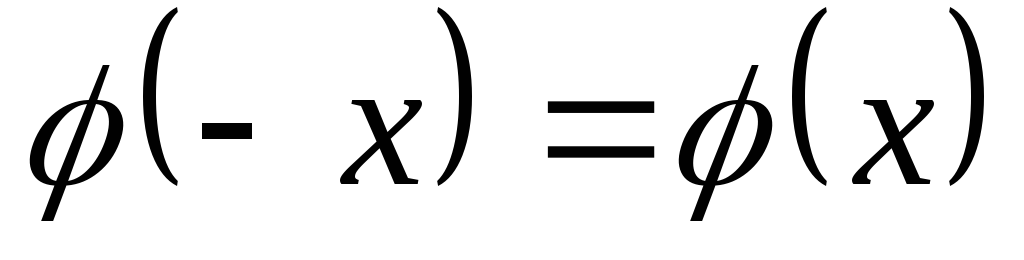3. при функція спадає до нуля;

4. .

Функція табульована для Длязначення функції практично рівне нулю.

Наслідок 2 (з інтегральної теореми Мавра-Лапласа). Якщо у схемі Бернуллі в кожному із незалежних випробувань подіяможе з’явитися з постійною ймовірністю, то ймовірність появи події не меншта не більшразів може бути знайдена заінтегральною формулою Мавра-Лапласа

, (7)

де

(8)

(9)

Функцію часом називають інтегральною функцією Лапласа. Вона має такі властивості:

1. функція є непарною, тобто ;

2. функція зростає для всіх;

3. 

Функція табульована дляДлязначення функції практично рівне 0,5.

Наслідок 3. Ймовірність того, що відносна частота появи події внезалежних випробуваннях відхилиться від ймовірностіпояви цієї події в одному випробуванні не більше, ніж наможна наближено визначити за формулою

(10)

Наближені локальну та інтегральну формули Мавра-Лапласа переважно застосовують у випадку, коли не дуже мале, приЯкщо ждуже мале, авелике, то використовують наближенуформулу Пуассона, яка дає краще наближення шуканої ймовірності:

(11)

(12)

де