Глава ііі: Аналітична геометрія

§1 Відповідність між геометричними образами та рівняннями

Як вже відомо із елементарного курсу математики, метод координат дає можливість встановити відповідність між деякими геометричними образами та рівняннями або їх нерівностями. В шкільних курсах розглядалась прямокутна декартова система координат на площині ху (тобто на площині, для всіх точок якої z=0) і говорилося про рівняння прямої, про рівняння параболи, про графік і т.д. Тепер, після введення прямокутної декартової системи координат в просторі, розглянемо це питання з більш загальних позицій.

Нехай в просторі задана прямокутна декартова система координат і потрібно встановити залежність між координатами будь-якої точки, що знаходиться на заданій відстані R від загальної точкиС(a, b, c).

Нехай Q є множина таких точок, тобто множина точок сфери S з центром в С і радіусом R. Нехай M(x, y, z) – довільна точка множини Q. Тоді , і тому

або

 (1)

Кожна точка множини Q, тобто кожна точка сфери, має координати, які відповідають рівнянню (1). Якщо точка N лежить не на сфері, а всередині неї, то , якщо точка N ззовні сфери, то . Рівняння (1) називається тому рівнянням, що відповідає заданій сфері, або просто рівнянням заданої сфери.

 

Визначення. Рівнянням, що відповідає заданій множині точок, називається рівняння, якому відповідають координати всіх точок множини, і не відповідають координати точок, що не належать заданій множині.

Визначення. Множиною точок, що відповідає заданому рівнянню, називається множина тих, і тільки тих точок, координати яких відповідають заданому рівнянню.

Розглянемо множину точок, які знаходяться на рівних відстанях від точки А(1, 3, -2) і від точки В(-1, 1, 0) (ця множина точок є площина, яка проходить через середину відрізку АВ і перпендикулярна до вектора ). Нехай М(x, y, z) довільна точка заданої множини. Згідно умови , і тому . Піднесемо обидві частини в квадрат і приведемо подібні члени, одержимо .

 

Якщо точка N не належить заданій множині точок , тоді

і

Таким чином, рівнянням, що відповідає заданій множині, є рівняння .

Розглянемо множину Q точок, що знаходяться на заданій відстані R від осі Z. Задана множина точок є нескінченна циліндрична поверхня, твірні якої паралельні осі Z і знаходяться від неї на відстаніR (рис.15).

 

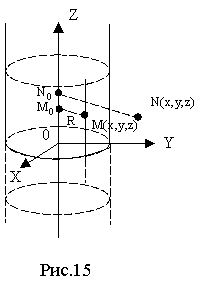
Складемо рівняння цієї поверхні. Нехай точка M(x, y, z) довільна точка множини Q; точка М₀ – проекція точки М на вісь Z – має координати (0, 0, Z). Згідно умови

 і тому або

 (2)

Отже, координати будь-якої точки множини Q задовольняють рівнянню (2). Нехай тепер точка N - яка-небудь точка, що не належить множині Q, і N₀ її проекція на вісь Z. Тоді , і тому . Ми довели тим самим, що рівняння (2) є рівнянням, що відповідає множині Q, тобто рівнянням нескінченної циліндричної поверхні, твірні якої паралельні осі Z і знаходяться від неї на відстані R.

 

Розглянемо множину Q точок площини, перпендикулярної осі Z, що проходить через точку М₀(0, 0, 2). Оскільки ця площина паралельна площині XY, то всі її точки мають одну і ту ж аплікату Z=2. Якщо ж візьмемо яку-небудь точку N(x, y, z), що не лежить на заданій площині, то для неї . Таким чином рівняння Z=2 є рівнянням заданої поверхні.

Із наведених прикладів видно, що рівнянням, в які входять три, дві і навіть одна невідома, в просторі відповідає деяка поверхня. Виключенням є випадки, коли поверхня “вироджується” в окремі точки, в лінію або взагалі представляє собою пусту множину точок. Так, наприклад, рівнянню відповідає одна точка – початок координат, рівнянню відповідає вісь Z, рівнянню - пуста множина точок.

Оскільки будь-яка лінія може бути представлена як перетин двох поверхонь, то лінія в просторі може бути задана системою двох рівнянь. Так, наприклад, системі рівнянь

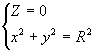
відповідає множина точок, що належить як площині Z=0, так і нескінченній циліндричній поверхні , тобто коло радіусом R, яке має центр на початку координат і лежить в площиніZ=0.

 

В багатьох задачах, особливо в задачах, пов’язаних з рухом, лінії задаються дещо по іншому. Нехай матеріальна точка рухається по якійсь лінії. Кожному моменту часу t в процесі руху відповідає деяке визначене положення точки М, що рухається. Нехай в просторі задана прямокутна декартова система координат. Тому кожному значенню t в процесі руху відповідає деякий радіус – вектор . Тим самим задана векторна функція . Векторне рівняння називають параметричним векторним рівнянням траєкторії.

Нехай і . Тоді для координат точки M(x, y, z), що рухається, маємо параметричне скалярне рівняння.

 (3)

 

Виключаючи t із перших та із останніх двох рівнянь системи (3), одержимо два рівняння, які зв’язують координати x, y, z довільної точки траєкторії, тобто рівняння двох поверхонь, що перетинаються по цій траєкторії.

В нашому прикладі параметром (допоміжною змінною), через яку виражався радіус-вектор будь-якої точки лінії, був час. Але параметром може бути не тільки час, але і довжина пройденої матеріальною точкою дуги, кут повороту і інші фізичні чи геометричні змінні. Важливо тільки те, щоб по кожному (в деякому проміжку, що розглядається) значенню параметра повністю визначалось положення змінної точки.

В цілому ряді задач поряд із завданням поверхонь і ліній необхідно розглядати і області, обмежені цими поверхнями або лініями.

Як правило, ці області можуть бути задані з допомогою одної або декількох нерівностей.

Нехай розглядається множина точок, які їй належать, в середині сфери радіусом R з центром в M₀(a, b, c) і нехай M(x, y, z) – довільна точка цієї множини. Очевидно

і тому

Всі точки заданої множини і тільки точки, які їй належать, мають координати, що відповідають одержаній нерівності. Тому вона може бути названа нерівністю, яка відповідає заданій множині точок.

Множині точок, які знаходяться між двома площинами, що перпендикулярні осі х і перетинають цю вісь в точках А(1, 0, 0) і В(3, 0, 0), відповідає система нерівностей 1<x<3. Множині точок, які знаходяться між концентричними колами з центром на початку координат, радіусами R₁=2 і R₂=3 і лежать в площині ху, відповідає система умов:

 і т.д.