§8 Розв'язки задач

Приклад 1. Не користуючись формулами диференціювання, знайти похідні функцій:

а) б) 

 

а) Надамо аргументу приріст , тоді y отримає приріст :

.

 

Знайдемо приріст функції:

 

Складаємо відношення

 

Знаходимо границю цього відношення при :

.

 

b) Знаходимо приріст функції:

;

 

Звідси

,

 

і

 

Таким чином

. ^

 

Приклад 2. Знайти похідні функції:

а) ;

 

б) ;

 

в) ;

 

г) ;

 

д) ;

 

е) ;

 

ж)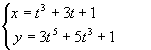 

 а) При диференціюванні необхідно врахувати, що перший доданок представляє степеневу функцію , її аргумент - логарифмічну функцію плюс сталу , а другий доданок - логарифмічну функцію , де :

 

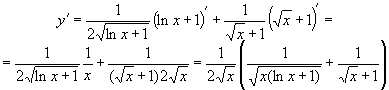
б) Це складна функція виду , де (називається проміжним аргументом). Використовуючи формулу диференціювання складної функції, одержимо:

;

 

в) Тут також складна функція , де Тоді

;

 

г) Згідно з правилом диференціювання частки двох функцій:

 

Враховуючи, що

 

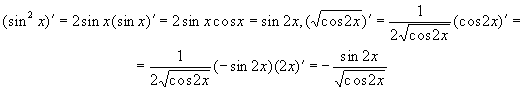
Отримаємо

;

 

д) За правилом диференціювання степенево-показникової функції:

.

 

Враховуючи, що , одержимо після перетворень

.

 

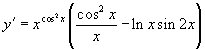Можна було б попередньо прологарифмувати заданий вираз по основі е

,

 

а потім продиференціювати обидві частини останньої рівності по . Оскільки є функцією від , тоді є складною функцією і . Отже,

;

 

Тобто,

 

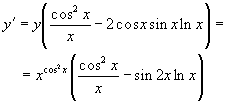
е) При диференціюванні неявної функції враховуємо, що є функція від 

 

Отже, ; .

 

Диференціюємо по обидві частини рівності, одержимо

 

Тобто,

;

 

ж) За правилом диференціювання функції, заданої параметрично

,

 

а тому знайдемо

 

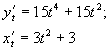
Отже,

 

Приклад 3. Обчислить значення похідної функції при :

 

а) ; б) .

 

а) Попередньо знайдемо похідну заданої функції: , а потім обчислюємо її значення в точці ;

;

 

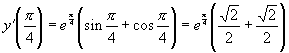б) Попередньо відмітимо, що . Тепер

;

 

Отже, .

 

Приклад 4. Задана крива . Скласти рівняння дотичних:

а) в точках перетину її з прямою ;

б) паралельно і перпендикулярно цій прямій.

1. Знайдемо точки перетину двох ліній, розв’язавши систему рівнянь:

,

 

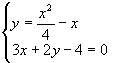звідки

 

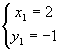
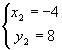
2. Знайдемо похідну функції . Значення похідної в знайдених точках ;.

 

3. Кутовий коефіцієнт заданої прямої , а прямої паралельної і перпендикулярної їй відповідно і . Тому точки, в яких дотична до кривої паралельна і перпендикулярна заданій прямій знаходяться із рівнянь

 ,

 

звідки відповідно і . Знайдемо ординати кривої в одержаних точках і . Відповідні рівняння дотичних будуть:

 

або і або .

 

Приклад 5. Знайти приріст і диференціал функції при і .

 

Приріст функції

.

 

Диференціал функції

.

 

При і маємо і . Різниця між і складає всього 0,02 або 0,5%.

 

Приклад 6. Знайти диференціал функції

:

 ^

 

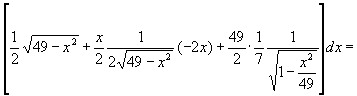
Приклад 7 Обчислити наближено: а) ;б) 

 

а) Припускаючи , знайдемо і у відповідності з формулою про наближені обчислення

.

 

Враховуючи, що , візьмемо і 

 

Тоді

;

 

б) Отримаємо спочатку наближену формулу для обчислення коренів будь-якої n-ої степені. Припускаючи , знайдемо

 ,

 

і у відповідності з (§6)

 

або

 

В заданому прикладі

 

За візьмемо число, найбільш близьке до 16,64, але щоб було відоме , при цьому повинне бути достатньо малим. Очевидно, необхідно взяти , (але, наприклад, не ). Отже,

 

За допомогою диференціала може бути розв’язана задача визначення абсолютної та відносної похибки функції по заданій похибці знаходження аргументу. Нехай необхідно обчислити значення заданої функції при деякому значенні аргументу , дійсна величина якого невідома, а відоме лише його наближене значення з абсолютною похибкою . Якщо замість дійсного значення візьмемо величину , то ми припустимося похибки, яка дорівнює

 

При цьому відносна похибка функції може бути обчислена (при достатньо малих ) за формулою

 (1)

 

або

,

 

де - еластичність функції (по абсолютній величині) - відносна похибка знаходження аргументу .

 

Приклад 8. Витрати бензину у (л) автомобіля на 100 км шляху в залежності від швидкості (км/год) описуються функцією .

Оцінить відносну похибку обчислення витрат бензину при швидкості 90 км/год з точністю до 5%.

Знайдемо еластичність функції (по абсолютній величині)

 

При і за формулою (1) відносна похибка ^

 

Приклад 9. З якою точністю може бути обчислений об’єм кулі, якщо її радіус заміряний з точністю до 2%?

 Об’єм кулі радіуса дорівнює . Знайдемо ;

 

і за формулою (1) маємо

Значним недоліком застосування диференціала в наближених обчисленнях є неможливість обчислення значень функцій з наперед заданою точністю. Цього недоліку немає при використанні рядів в наближених обчисленнях.