1. Система однорідних рівнянь 1-ого порядку завжди сумісна.

2. Якщо визначник системи однорідних рівнянь 1-ого порядку дорівнює нулю, тоді система має нескінченну множину розв 'язків.

Приклад 2

 

Розв’язок

 

 

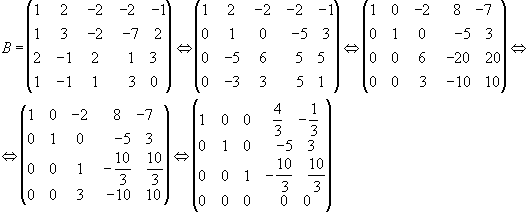
Система рівнянь, що відповідає одержаній матриці, має вигляд:

 

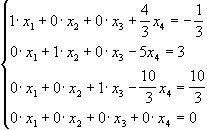
Система сумісна, х₄=t довільно. Система має нескінченну множину розв`язків

причому t - довільне число.

Відмітимо, що якби вільні члени в рівняннях були іншими, ніж задано в умові, система могла б бути несумісною. Нехай, наприклад, b₄=1. Тоді перетворена матриця система буде

 

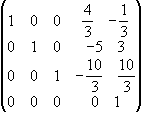
і останнє рівняння системи набуде такого вигляду 0 х₁+0 х₂+0 х₃+0 х₄=1, що не має змісту.

 

Приклад 3.

 

Розв`язок.

 

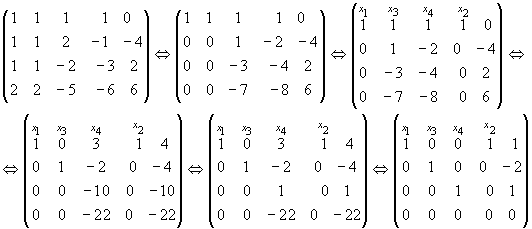
Система сумісна, х₂=t довільно; x₁=1-t, x₂=t, x₃=-2, x₄=1.

 

Розібраний метод без будь-яких змін переноситься і на той випадок, коли число невідомих не співпадає з числом рівнянь.

 

ІІ. Приклади розв`язку задач

1.20. Розв`язати систему

Обчислимо визначник системи

 

Оскільки визначник системи відмінний від нуля, застосуємо правило Крамера. Для обчислення визначника detB₁ замінимо стовпець визначника системи стовпцем з вільних членів . Маємо

 

Визначник detB₂ одержимо заміною стовпця визначника системи стовпцем із вільних членів:

 

Згідно правила Крамера знаходимо ; 

Сукупність чисел (5;-4) являється єдиним розв`язком даної системи.

1.21. Знайти розв`язки системи

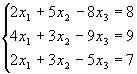
Визначник з коефіцієнтів системи відмінний від нуля:

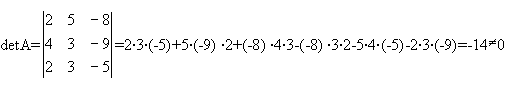
Тому можна застосувати правило Крамера

 

звідси знаходимо ; ; 

Сукупність чисел (3, 2, 1) являється єдиним розв`язком системи.

1.22. Розв`язати систему

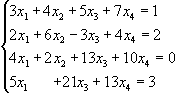
Випишемо розширену матрицю системи

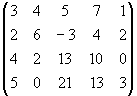 /IVp+II-I-III/ ~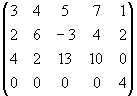 

Неважко бачити, що визначник з коефіцієнтів системи дорівнює нулю, оскільки 4-ий рядок його складається з нулів. Останній рядок розширеної матриці свідчить про те, що система не сумісна.

1.23. Розв’язати систему

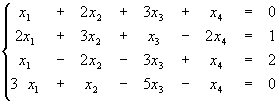
Випишемо розширену матрицю системи

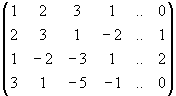 /IIp.-2·I, IIIp.-I, IVp.-II-III/ ~  ~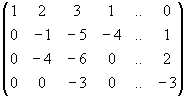

/поділимо ІІІр. на (-3), IVp. на (-3)/

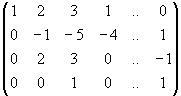~ /ІІІр.+2·ІІ/ ~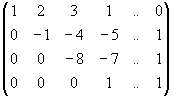 

 

В результаті всіх перетворень дана система лінійних рівнянь звелася до трикутного виду.

 

Вона має єдиний розв`язок.

х₃=1 х₄=-1 х₂=-2 х₁=2 ^

1.24.

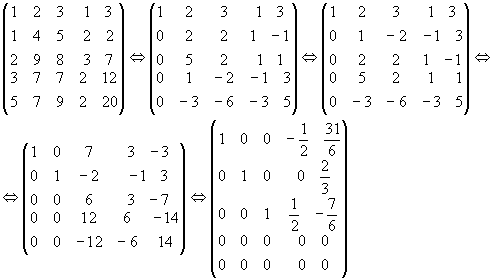
Рівняння сумісні, х₄=t довільно, 

 

1.25. Знайти роз’язки системи

 

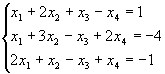
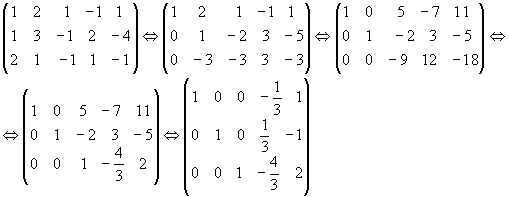
Система сумісна, х₄=t довільно, 

 

1.26. Розв’язати систему

 

Система сумісна, х₄=t довільно, x₁=t, x₂=-2t, x₃=0, x₄=t.

 

 

§ 6 Ранг матриці, теорема про сумісність систем рівнянь першого порядку

Для дослідження багатьох питань, пов`язаних з розв’язком систем рівнянь 1-ого порядку, часто вводять поняття ранг матриці.

Визначення. Рангом матриці називається найвищий порядок відмінного від нуля визначника квадратної субматриці, отриманої із заданої матриці викреслюванням деяких рядків і стовпців.

Розглянемо, наприклад, матрицю

 

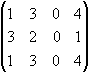
Викресленням будь-якого числа рядків і стовпців неможливо із заданої матриці одержати квадратну матрицю порядку вище 3-го. Звідси, ранг її не може бути більше трьох. Але, викреслюючи один із стовпців, ми будемо одержувати квадратні матриці, які мають два однакових рядка, а тому їх визначники дорівнюють нулю. Звідси, ранг вихідної матриці менше 3-х. Викресливши, наприклад, 3-й і 4-й стовпець і 3-й рядок, одержимо квадратну матрицю , визначник якої не дорівнює нулю. Таким чином, всі визначники субматриці 3-го порядку дорівнюють нулю, але серед визначників матриць 2-го порядку є відмінний від нуля. Тим самим ранг вихідної матриці дорівнює двом.

Доведемо теорему: ранг матриці не змінюється при лінійних операціях з її рядками.

Дійсно, лінійні операції з рядками якої-небудь матриці приводять до тих же лінійних операцій з рядками будь-якої субматриці. Але, як вказано вище, при лінійних операціях з рядками квадратних матриць визначники цих матриць одержуються один із другого множенням на число, відмінне від нуля. Звідси, нульовий визначник залишається нульовим, а відмінний від нуля - відмінним від нуля, тобто не може змінитися найвищий порядок відмінного від нуля визначника субматриць. Не впливає, очевидно, на ранг матриці і перестановка стовпців, оскільки така перестановка може впливати лише на знак відповідних визначників.

Із доведеної теореми виходить, що розглянуті в минулому параграфі перетворені матриці мають той же ранг, що і вихідні. Тому ранг основної матриці системи рівнянь першого порядку дорівнює числу одиниць на головній діагоналі перетвореної матриці.

Доведемо тепер теорему про сумісність систем рівнянь 1-ого порядку (теорема Кронекера-Капеллі): для того щоб система рівнянь 1-ого порядку була сумісна, необхідно і достатньо, щоб ранг розширеної матриці співпадав з рангом основної матриці.

Нехай ранг основної матриці системи дорівнює k. Якщо ранг розширеної матриці системи також дорівнює k, тоді це означає, що або система містить тільки k рівнянь, або - всі числа (i= k+1, ..., k) в перетвореній матриці дорівнюють нулю (в противному випадку ранг розширеної матриці перетвореної, а тому і вихідної системи був би k +1)

 

Нехай ранг перетвореної (а тому і вихідної) розширеної матриці системи більше k, тобто більше, ніж число одиниць на головній діагоналі перетвореної матриці. Тоді існує хоча б одна субматриця (k+1)-го порядку, визначник якої не дорівнює нулю. Така субматриця може бути одержана тільки додаванням до одиничної матриці порядку k (що знаходиться в лівому верхньому куту перетвореної матриці) якого-небудь одного рядка і стовпця, який складається із перших k вільних членів рівнянь перетвореної системи і будь-якого одного вільного члена із наступних n-k рівнянь. Щоб визначник вказаної субматриці був відмінний від нуля, відмінним від нуля повинен бути і цей останній доданий елемент, тобто число (i=k+1, ..., k). Але, як було доведено раніше, в цьому випадку система несумісна. Отже, система сумісна тоді і тільки тоді, коли ранг основної матриці співпадає з рангом розширеної матриці.