2.2. Задача про миттєву швидкість

Розглянемо нерівномірний прямолінійний рух тіла, що розпочинається в момент часу . Вважатимемо, що шлях, подоланий тілом за час , дорівнює . Функція називаєтьсязаконом руху тіла.

Шлях , який подолає тіло за відрізок часу , знаходиться як

 

Середньою швидкістю руху за проміжок часу називається відношення

в якому легко пізнати диференціальне відношення.

Миттєвою швидкістю руху в момент називається границя цього відношення, якщо , тобто

.

 

Отже, похідна від шляху за часом дорівнює миттєвій швидкості прямолінійного руху тіла.

 

2.3. Задачі про витрати виробництва та виручку

Нехай - витрати виробництва однорідної продукції – деяка функція кількості продукції х. Зазначимо, що кількості продукції відповідають витрати виробництва продукції . Отже, диференціальне відношення, що характеризує середній приріст витрат виробництва,

Воно відбиває приріст витрат виробництва на одиницю приросту кількості продукції.

Границя

називається граничними витратами виробництва.

Нехай - виручка від продажу х одиниць товару. Міркування, аналогічні до попередніх, приводять до границі

яку називають граничною виручкою.

§3. Правила диференціювання

3.1 Диференціювання суми, добутку й частки

Теорема 1. Якщо функції і диференційовані в точці х, то функції (в останньому випадку припускається, що ) також диференційовані в цій точці і мають місце формули:

а) ;

 

б) ;

 

в) .

 

Доведення. а) Надамо х деякого приросту . Тоді функції і матимуть прирости і , а функція - приріст . І, отже,

 

тобто функції дійсно диференційовані в точці х , і має місце формула а).

б) Надамо х деякого приросту . Тоді функції і матимуть прирости і , а функція - приріст

 

І, отже,

 

Зазначимо, що функція неперервна в точці х, оскільки вона диференційована в цій точці, а тому при . Переходячи до границі при в останній рівності, отримаємо , тобто функція дійсно диференційована в точці х і має місце формула б).

в) Надамо х деякого приросту , тоді функція і матимуть прирости і , а функція - приріст

Переходячи до границі при в останній рівності, отримаємо , тобто функція дійсно диференційована в точці х і має місце формула в).

 

Наслідок. Припустимо, у формулі б) , тоді і , тобто сталий співмножник можна виносити за знак похідної.

3.2. Диференціювання складної функції

Теорема 2. Нехай - складна функція, де і - диференційовані функції своїх аргументів. Точніше, зовнішня функція в точці має похідну (по U) , а внутрішня функція у точці х має похідну (по х) . Тоді складна функція - диференційована в точці х, причому її похідна обчислюється за формулою

 

або коротко

 чи 

 

Доведення. Надамо х деякого приросту . Тоді функція дістане приріст , а функція - приріст .

За умови маємо

 

Переходячи в цій рівності до границі при , отримаємо

 

що й потрібно довести.

При доведенні враховано, що функція неперервна в точці х, оскільки вона диференційована в цій точці і, отже, при .

 

Зауваження. Припущення, що досить малому відповідає , звичайно ж, істотне. Проте, якщо трапиться, що (до речі, цей випадок зустрічається рідко), то формулу диференціювання складної функції неважко встановити трохи іншим шляхом.

 

Наслідок. (диференціювання оберненої функції). Нехай функція обернена по відношенню до функції , причому функції і мають похідні відповідно в точках х і . Встановимо зв’язок між похідними і .

 

Оскільки при всіх х, то за правилом диференціювання складної функції похідні від обох частин цієї рівності , звідки або коротко чи .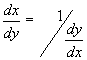

 

Останні формули мають простий геометричний зміст. Кутовий коефіцієнт дотичної до графіка функції у точці , а кутовий коефіцієнт до графіка функції в точці (рис.2).

 

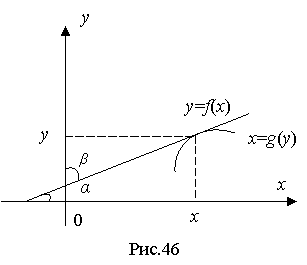
Очевидно, що , а тому або .