Приклади розв’язання задач

1.1. Обчисліть визначник другого порядку

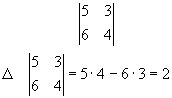
1.2. Обчисліть визначник третього порядку

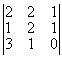
Згідно правила трикутника, маємо

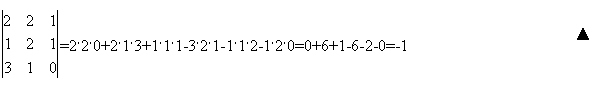
1.3. Обчисліть визначник третього порядку

Розклавши визначник по елементах 1-го рядка, одержимо

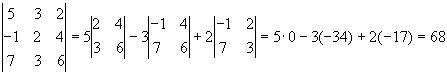
1.4. Обчисліть попередній приклад інакше, використавши властивості визначників.

До елементів 1-го рядка додамо відповідні елементи 2-го рядка, помножені на 5, а до елементів 3-го рядка - відповідні елементи 2-го рядка, помножені на 7.

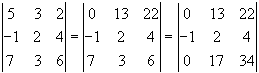
Розклавши визначник по елементах 1-го стовпця, одержимо

1.5. Обчисліть визначник

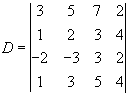
Виконаємо такі дії: 1) до елементів 1-го рядка додамо помножені на -3 відповідні елементи 2-го рядка; 2) до елементів 3-го рядка додамо подвоєні елементи 2-го рядка; 3) до елементів 4-го рядка додамо відповідні елементи 2-го рядка, помножені на -1. Тоді вихідний визначник перетвориться до вигляду.

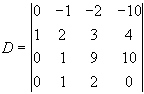
Розклавши цей визначник по елементах 1-го стовпця, маємо

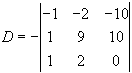
Додамо до елементів 1-го рядка елементи 3-го рядка і віднімемо від елементів 2-го рядка елементи 3-го рядка, одержимо

Розкладемо визначник по елементах 1-го стовпця.

1.6. Обчисліть визначник п^’ятого порядку

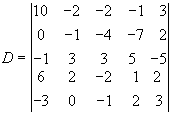
Для перетворення в нуль всіх елементів (крім одного) будь-якого рядка чи стовпця, вибираємо той рядок або стовпчик, який складається з найменших чисел. У визначнику таким буде другий стовпчик. Залишимо в ньому без змін елемент а₂₂=-1, а всі інші перетворимо в нулі. Для цього виконаємо: (Ір+(-2)* IIр, IIIp+3 IIр, ІVр+2 Пр).

Одержимо:

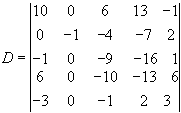
Розкладемо визначник по елементах другого стовпця.

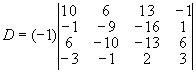
В одержаному визначнику вже 4-го порядку з найменших елементів складається 4-ий рядок. Перетворимо в нулі всі його елементи, крім а₄₂=-1. Для цього виконаємо

(І_ст+(-3)ІІ_ст, ІІІ_ст+2 ІІ_ст, ІV_ст+3 ІІ_ст). В результаті одержимо:

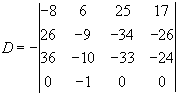
Розкладемо визначник по елементах четвертого рядка

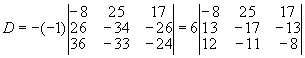
(Ми винесли за знак визначника спільний множник з елементів другого рядка і спільний множник з елементів третього рядка).

Для зменшення елементів цього визначника додамо перший стовпець до другого та третього:

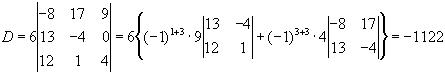
Останній визначник розклали по елементах третього стовпця.

1.7. Обчислити визначник n-го порядку, звівши його до трикутного вигляду:

.

 

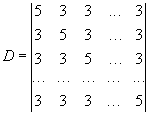 Віднімемо І рядок від усіх інших.

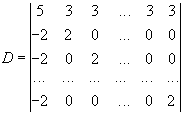 До І стовпця додамо суму всіх інших.

 

 

§5 Розв'язок систем n рівнянь із n невідомими

5.1. Правило Крамера

Встановивши основні властивості і способи обчислення визначників матриць будь-якого порядку, повернемося до основної задачі - розв'язку і дослідження систем рівнянь 1-ого порядку. Почнемо вивчення цього питання із розбору того основного випадку, коли число рівнянь співпадає з числом невідомих.

Нехай задана система:

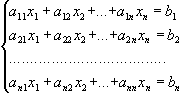 (1)

 

Будемо вважати, що система (1) має який-небудь розв'язок і потрібно тільки знайти його. Позначимо через А основну матрицю системи.

 

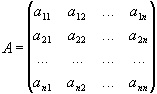
Помножимо всі члени 1-го рівняння системи (1) на А₁₁ - алгебраїчне доповнення елементу а₁₁ матриці А, всі члени 2-го рівняння системи (1) на А₂₁ - алгебраїчне доповнення елементу а₂₁матриці А, нарешті, всі члени n-го рівняння системи (1) на А_n1 - алгебраїчне доповнення елементу а _n1 матриці А. Тоді одержимо систему

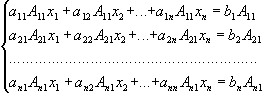 (1')

 

Додамо почленно всі рівняння системи, одержимо

(a_i1A_i1)x₁+(a_i2A_i1)x₂+...+(a_inA_i1)x_n=b_iA_i1

Згідно теореми про алгебраїчні доповнення маємо

a_i1A_i1=det A a_i2A_i1=0, ........., a_inA_i1=0

Тому одержане рівняння можна переписати у вигляді 

Розглянемо матрицю

,

 

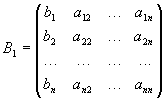отриману із матриці А заміною елементів 1-го стовпця стовпцем вільних членів рівнянь системи. Розкладаючи det B₁ по елементах 1-го стовпця, одержимо det B₁=b_iA_i1 , а тому Х_1 det A= det B₁

Аналогічно, помноживши рівняння системи (1) відповідно на А_і2 (і=1, 2, ... n) і додаючи їх, одержимо X_2 det A=det B₂ ,

 

де

,

 

Поступивши таким чином і в подальшому, одержимо систему рівнянь

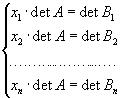 (2)

 

де матриця В_k одержана із А заміною k-го стовпця стовпцем вільних членів. Очевидно, будь-який розв'язок системи (1) є і розв'язком системи (2).

Будемо вважати тепер, що визначник основної матриці системи не дорівнює нулю. Тоді система (2) має єдиний розв'язок

 (3)

 

Нагадаємо, що формули (3) одержані з припущенням, що система (1) має розв'язок. Безпосередньою підстановкою знайдених значень Х_і в систему (1) можливо переконатися в тому, що вони є розв'язком системи (1) і, отже, в припущенні, що, система (1) має розв'язок і до того ж єдиний.

 

Теорема (теорема Крамера): якщо визначник основної матриці системи п рівнянь 1-го порядку з п невідомими відмінний від нуля, тоді система має єдиний розв'язок. При цьому значення кожного із невідомих дорівнює частці від ділення визначників двох матриць: в знаменнику стоїть визначник основної матриці системи, а в чисельнику визначник матриці, одержаної із основної матриці системи заміною стовпця, що відповідає вибраному невідомому, стовпцем вільних членів.

Із цієї теореми виходить, що якщо система рівнянь однорідна, тобто вільні члени у всіх рівняннях системи дорівнюють нулю, і якщо визначник основної матриці системи відмінний від нуля, тоді система має тільки нульовий розв'язок. Дійсно, в такому випадку, матриці, визначники яких стоять в чисельнику формул (3), містять стовпець, який включає в себе лише нулі, і, отже, всі числа Х_ідорівнюють нулю. Із доведеного випливає наступна теорема:

 

Якщо система п однорідних рівнянь 1-го порядку з п невідомими має хоча б один ненульовий розв'язок, тоді визначник основної матриці системи дорівнює нулю. Дійсно, якби цей визначник був не рівний нулю, тоді система мала б тільки нульовий розв'язок, що суперечить умові.

В подальшому ми доведемо, що рівність нулю визначника система є не тільки обов'язкова, необхідна умова існування ненульового розв'язку, але і умова, достатня для існування такого розв'язку. Інакше кажучи, якщо визначник системи однорідних рівнянь дорівнює нулю, тоді система має ненульовий розв'язок (і при цьому нескінченну множину таких розв'язків).