§4 Дослідження функцій

 

4.1. Умови монотонності функцій

Визначення 1. Функція називається зростаючою (спадною) на деякому проміжку Х, якщо для будь-яких виконана нерівність (відповідно ).

 

Теорема 1 (достатні умови монотонності). Якщо функція диференційована на проміжку Х і на Х, то функція зростаюча (спадна) на цьому проміжку.

 

Доведення. Нехай для конкретності на Х і - будь-які точки з Х, причому . За формулою Лагранжа , де .

 

Оскільки і , то або , тобто функція зростає на Х.

Випадок, коли на Х, досліджується аналогічно.

 

4.2. Умови локального екстремуму

 

Визначення 2. Точка називається точкою строгого локального мінімуму (максимуму) функції , якщо при всіх з деякого -околу точки виконується нерівність

.

 

Аналогічно, якщо в деякому -околі точки виконується нерівність

,

 

то точка називається точкою локального мінімуму (максимуму). Часто для скорочення слово локальний не вживають.

Точки мінімуму й максимуму функції називають точками екстремуму, а значення функції в цих точках – її екстремумами.

 

Теорема 2 (необхідні умови екстремуму). Якщо точка є точкою екстремуму функції і в цій точці функція диференційована, то .

 

Доведення. Нехай для конкретності - точка максимуму, тоді при досить малих і , а отже,

 

Оскільки ж функція диференційована в точці , то

.

 

Випадок, коли - точка мінімуму, досліджується аналогічно.

Теорема 2 має простий геометричний зміст: дотична до графіка диференційованої функції у відповідній точці паралельна осі Ох.

 

Зауваження 1. Якщо , то звідси ще не випливає, що - точка екстремуму. Наприклад, для функції похідна і . Проте , очевидно, не є точкою екстремуму.

 

Зауваження 2. Точка , в якій функція недиференційована, також може бути точкою екстремуму. Наприклад, функція не має похідної в точці , але ця точка є для неї точкою мінімуму.

Точки, в яких похідна дорівнює нулю, називаються стаціонарними. Стаціонарні точки, а також точки, де функція визначена, але її похідна не існує, називаються критичними. Саме серед них слід шукати точки екстремуму.

 

Теорема 3 (достатні умови строгого екстремуму першого типу). Нехай функція неперервна в деякому -околі точки : , диференційована у ньому, крім, можливо, самої точки . Тоді, якщо при і при , то точка є точкою строгого мінімуму (максимуму).

Коротко цю теорему формулюють таким чином: якщо в точці похідна змінює знак з мінуса на плюс (з плюса на мінус), то - точка строгого мінімуму (максимуму)

 

Доведення. Нехай для конкретності при і при .

 

Спочатку розглянемо . Застосуємо формулу Лагранжа до функції на відрізку . Маємо

,

 

де . Оскільки і, тоабо при .

 

Якщо ж , то застосовуючи формулу Лагранжа до функції на відрізку , матимемо

,

 

де . Оскільки і , то або при .

 

Таким чином, для будь-якого з - околу точки , а це й означає, що точка є точкою строгого мінімуму.

Випадок зміни знаку похідної з плюса на мінус досліджується аналогічно.

Зауваження. Якщо має однакові знаки на інтервалах і , то не є точкою строгого екстремуму.

 

Теорема 4 (друга достатня ознака екстремуму). Якщо в околі точки друга похідна неперервна, причому , а , то функція має в точці максимум, коли , і мінімум, коли .

Доведення. Нехай . Зважаючи на неперервність , існує деякий окіл точки , в якому . Тому в цьому околі функція буде спадною, бо її похідна - - від’ємна. Але ж при , отже, при переході (зліва направо) через точку функція змінює знак з плюса на мінус. А це означає, що в точці функція має максимум.

Аналогічно доводиться, що, коли і , то - мінімум функції .

Якщо ж в деякій критичній точці , то друге правило не застосовне і дослідження слід проводити за допомогою першої похідної (спираючись на теорему 3).

 

Приклад 3. Дослідити на максимуми та мінімуми.

1. Знаходимо похідну .

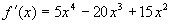1. Прирівнюємо до нуля і знаходимо її корені, тобто критичні точки

3. Обчислюємо другу похідну

4. Підставляючи у вираз другої похідної знайдені корені першої похідної, отримаємо 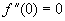(правило не застосовне), 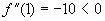(максимум), (мінімум).

Через те що при , вдаємося до першого правила. Маємо при , при (але ) .

Похідна не змінює знака, екстремуму в точці немає.

За допомогою теорії максимумів та мінімумів функції розв’язуються численні задачі з геометрії, економіки, механіки та з інших наук.