
- •Конспект лекцій з курсу
- •§2 Визначники матриць другого порядку
- •§3. Визначники матриць третього порядку
- •§ 4 Визначники матриць вищих порядків
- •Приклади розв’язання задач
- •§5 Розв'язок систем n рівнянь із n невідомими
- •5.1. Правило Крамера
- •5.2. Розв'язок і дослідження систем рівнянь першого порядку методом повного виключення (Метод Гаусса).
- •1. Система однорідних рівнянь 1-ого порядку завжди сумісна.
- •2. Якщо визначник системи однорідних рівнянь 1-ого порядку дорівнює нулю, тоді система має нескінченну множину розв 'язків.
- •§ 6 Ранг матриці, теорема про сумісність систем рівнянь першого порядку
- •Іі. Приклади розв`язку задач
- •Обчислення рангу матриці методом облямування
- •§ 7 Основні операції з матрицями
- •Приклади розв`язку задач
- •§ 8 Обернена матриця, розв`язок матричних рівнянь
- •Іі. Приклади розв`язку задач
- •§9. Модель багатогалузевої економіки
- •Глава іі: Векторна алгебра
- •§1 Основні поняття
- •§2 Лінійні операції з векторами.
- •§ 3 Лінійна залежність та лінійна незалежність системи векторів
- •Приклади розв‘язку задач
- •§4 Проекція вектора на ось
- •§5 Прямокутна декартова система координат в просторі
- •§6 Скалярний добуток векторів
- •§7 Векторний добуток векторів
- •§8 Мішаний добуток векторів
- •Іі. Приклади розв’язку задач
- •Глава ііі: Аналітична геометрія
- •§1 Відповідність між геометричними образами та рівняннями
- •§ 2 Лінійні образи - площина і пряма
- •§ 3 Лінії другого порядку
- •Приклади розв`язку задач
- •§4 Перетворення координат на площині. Застосування перетворення координат до спрощення рівнянь кривих другого порядку.
- •§5 Циліндричні поверхні з твірними, паралельними координатним осям; поверхні другого порядку
- •5.1. Дослідження форми еліпсоїда
- •5.2. Дослідження форми однопорожнинного гіперболоїда
- •5.3. Дослідження формули двопорожнинного гіперболоїда
- •5.4. Дослідження формули еліптичного параболоїда
- •5.5. Дослідження форми гіперболічного параболоїда
- •6. Дослідження форми конуса 2-го порядку
- •Приклади розв`язку задач
- •§6 Полярна система координат на площині. Циліндрична і сферична системи координат в просторі
- •6.1. Полярна система координат на площині
- •6.2. Циліндрична система координат
- •6.3. Сферична система координат
- •Приклади розв’язку задач
- •Розділ іі. Вступ до математичного аналізу
- •Глава IV: Функції
- •§1 Поняття множини
- •§2. Абсолютна величина дійсного числа
- •§3. Поняття функції
- •§4 Застосування функцій в економіці
- •Розв’язок задач
- •Глава V: Границя і неперервність
- •§1 Поняття границі послідовності
- •1.1 Збіжні послідовності
- •1.2 Нескінченно малі і нескінченно великі.
- •§2 Основні властивості збіжних послідовностей
- •§3 Поняття границі функції
- •3.1 Визначення границі функції
- •3.2 Односторонні границі
- •3.3 Границя функції на нескінченності і нескінченні границі
- •§4 Властивості границь
- •§5 Перша і друга важливі границі
- •5.1 Перша важлива границя
- •5.2 Друга важлива границя
- •Задача про неперервне нарахування процентів
- •§6 Нескінченно малі та нескінченно великі функції
- •§7 Неперервність функції
- •Розв’язки задач
- •Розділ ііі. Диференціальне числення
- •Главаvi: Похідні та диференціали
- •§ 1 Поняття похідної
- •§2 Зміст похідної
- •2.1. Задача про дотичну до кривої
- •2.2. Задача про миттєву швидкість
- •2.3. Задачі про витрати виробництва та виручку
- •§3. Правила диференціювання
- •3.1 Диференціювання суми, добутку й частки
- •3.2. Диференціювання складної функції
- •§4. Диференційованість елементарних функцій
- •§5. Похідні вищих порядків
- •§ 6. Диференціал функції
- •§ 7. Диференціали вищих порядків
- •§8 Розв'язки задач
- •§ 9 Економічний зміст похідної.
- •Глава 7: Застосування похідних до дослідження функцій
- •§ 1 Загальні властивості функцій, неперервних на замкненому проміжку
- •§ 2 Теореми про середнє значення
- •§ 3 Правила Лопіталя
- •§4 Дослідження функцій
- •4.1. Умови монотонності функцій
- •4.3. Знаходження найменшого й найбільшого значень
- •4.4 Опуклість, угнутість та точки перегину кривої
- •3.5. Асимптоти. Дослідження графіка функції в цілому
- •§ 5 Застосування похідної в економічній теорії.
- •§ 5. Розв’язки задач
Розв’язки задач
Попередні
вказівки. Для
засвоєння поняття границі функції
доцільно використати геометричну
інтерпретацію: при цьому змінна ![]() зображається
“рухомою” точкою на осі Ох,
а відповідні значення функції f(х) наближаються
і залишаються як завгодно близькими до
точки А на
осі Оу.
Якщо мова йде про однобічні границі, то
в такому випадку змінна х наближається
до точки а по
осіОх зліва
(
зображається
“рухомою” точкою на осі Ох,
а відповідні значення функції f(х) наближаються
і залишаються як завгодно близькими до
точки А на
осі Оу.
Якщо мова йде про однобічні границі, то
в такому випадку змінна х наближається
до точки а по
осіОх зліва
(![]() ,
тобто
,
тобто ![]() , х
< а )
або справа (
, х
< а )
або справа (![]() ,
тобто
,
тобто ![]() , х
> а ).
Слід звернути увагу, що у визначенні
границі функції не враховується значення
функції в граничній точці,
, х
> а ).
Слід звернути увагу, що у визначенні
границі функції не враховується значення
функції в граничній точці, ![]() f(х) не
залежить від величини f(х0),
яка може й не існувати. Звідси випливає,
що під знаком границі можна робити
тотожні перетворення аналітичного
виразу, незважаючи на поведінку функції
в граничній точці (тобто, можна скорочувати
дроби на множник, що перетворюється в
нуль в граничній точці ).
f(х) не
залежить від величини f(х0),
яка може й не існувати. Звідси випливає,
що під знаком границі можна робити
тотожні перетворення аналітичного
виразу, незважаючи на поведінку функції
в граничній точці (тобто, можна скорочувати
дроби на множник, що перетворюється в
нуль в граничній точці ).
Якщо ![]() ,
, ![]() ,
то кажуть, що вираз
,
то кажуть, що вираз![]() при
при ![]() є
невизначеність типу
є
невизначеність типу ![]() .
У цьому випадку для знаходження
.
У цьому випадку для знаходження ![]() застосовують
спеціальні прийоми, а сам процес
знаходження границі називають розкриттям
невизначеності.
застосовують
спеціальні прийоми, а сам процес
знаходження границі називають розкриттям
невизначеності.
Зустрічаються
невизначеності типу: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
При
цьому невизначеності типу ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() зводяться
до невизначеності типу
зводяться
до невизначеності типу ![]() або
або ![]() .
.
Приклад.
Знайти:
а) ![]()
![]() б)
б) ![]()
![]()
в)![]()
![]() г)
г)![]()
![]()
![]()
д) ![]()
![]() е)
е) ![]()
![]()
а)
Підстановка граничного значення
аргументу х=-3
призводить до невизначеного виразу
типу ![]() .
.
Для
усунення цієї невизначеності розкладемо
чисельник і знаменник дробу на множники
і скоротимо дріб на множник (х+3).Таке
скорочення тут можливе, оскільки множник
(х + 3) відмінний від нуля при ![]() :
:
![]()
![]() =
=![]()
![]() =
=![]()
![]() =
=![]() =
=![]() .
.
б)
Якщо ![]() ,
вираз
,
вираз ![]() дає
невизначеність типу
дає
невизначеність типу ![]() .
Для її усунення помножимо і розділимо
цей вираз на (
.
Для її усунення помножимо і розділимо
цей вираз на (![]() +
+ ![]() )
:
)
:
![]() (
(![]() -
-![]() )=
)=![]()
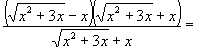
![]()
![]() =
=![]()
![]() .
.
в) У цьому випадку ні чисельник, ні знаменник не мають границі, тому що обидва необмежено зростають.
Перетворимо
попередньо вираз під знаком границі,
поділивши чисельник та знаменник на ![]() .
Тоді одержимо
.
Тоді одержимо
![]()
![]()
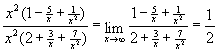
Зауваження
. Якщо
нам треба знайти границю відношення
двох многочленів при ![]() ,
то необхідно попередньо поділити
чисельник та знаменник на максимальні
ступені, що входять в них. Тоді
,
то необхідно попередньо поділити
чисельник та знаменник на максимальні
ступені, що входять в них. Тоді
![]()
![]() =
= ![]()
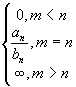
г)
Позначимо ![]() 5
х = у. Тоді 5 х =
5
х = у. Тоді 5 х = ![]() і
і ![]() при
при ![]() .
Застосовуючи властивості границь і
формулу першої важливої границі
.
Застосовуючи властивості границь і
формулу першої важливої границі
![]() ,
маємо:
,
маємо:
![]()
![]()
![]()
д) Перетворимо вираз
![]()
При ![]() такий
вираз дає невизначеність типу
такий
вираз дає невизначеність типу ![]()
Для
усунення її застосуємо формулу другої
важливої границі ![]() .
.
Тоді
маємо: 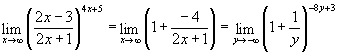 ;
;
де ![]() ,
, ![]() і
і ![]() при
при ![]()
Переходячи
до змінної ![]() ,
одержимо:
,
одержимо:
![]()
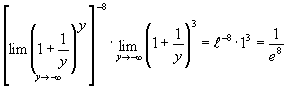 .
.
е) ![]() =
=![]()
При
обчисленні границі ми скористалися
теоремою про граничний перехід під
знаком логарифма, оскільки для неперервної
функції справедливо: ![]()
Приклад. Знайти:
а) ![]() ;
б)
;
б) ![]() ;
;
в) ![]() г)
г) ![]()
а) ![]() =0,
оскільки добуток нескінченно малої
величини х (при
=0,
оскільки добуток нескінченно малої
величини х (при ![]() )
на обмежену функцію
)
на обмежену функцію ![]()
![]() є
величина нескінченно мала.
є
величина нескінченно мала.
Відмітимо,
що ця границя не може бути обчислена за
допомогою теореми про границі добутку,
оскільки ![]() не
існує ( при
не
існує ( при ![]() аргумент
косинуса
аргумент
косинуса ![]() змінюється
неперервно вздовж числової осі до
нескінченності, при цьому
значення
змінюється
неперервно вздовж числової осі до
нескінченності, при цьому
значення ![]() коливається
від –1 до 1 і
від 1 до-1, не прямуючи ні до якого числа
(границі)).
коливається
від –1 до 1 і
від 1 до-1, не прямуючи ні до якого числа
(границі)).
б) 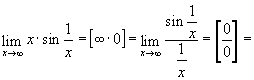
![]()
![]() (Тут
виконана заміна
(Тут
виконана заміна ![]() при
при ![]() ).
).
в) розглянемо два випадки:

Оскільки ![]()
При ![]() маємо
невизначеність
маємо
невизначеність ![]() ,
при цьому розділимо чисельник і знаменник
на
,
при цьому розділимо чисельник і знаменник
на ![]() і
використаємо теорему про границі,
одержимо:
і
використаємо теорему про границі,
одержимо:
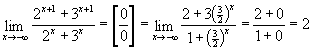
г) 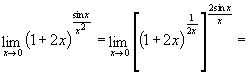

Приклад . Довести
неперервність функції ![]() в
точці х=0
і встановити характер точки розриву
функції в цій точці:
в
точці х=0
і встановити характер точки розриву
функції в цій точці:
а) ![]() ;
б)
;
б) 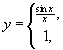 якщо
якщо ![]() ;
в)
;
в) ![]() ;
;
а)
При х=0 функція f(x) не
визначена, отже вона не неперервна в
цій точці. Оскільки ![]() ,
і відповідно границі функції зліва і
справа від точки х=0
скінченні і рівні, тобто
,
і відповідно границі функції зліва і
справа від точки х=0
скінченні і рівні, тобто ![]() ,
то х=0 – точка
усунутого розриву першого роду.
,
то х=0 – точка
усунутого розриву першого роду.
б)
В порівнянні з попереднім прикладом
тут функція до визначена в точці х=0
так, що ![]() ,
отже, така функція неперервна в цій
точці.
,
отже, така функція неперервна в цій
точці.
в)
При х=0
функція f(х) не
визначена. Оскільки границі функції
зліва і справа від точки х=0
скінченні, тобто ![]() ;
; ![]() ;
(
;
(![]() при
при ![]() ),
то в точці х=0 функція f(x)має
розрив першого роду.
),
то в точці х=0 функція f(x)має
розрив першого роду.
