Matta, Boyd. The quantum theory of atoms in molecules

32 1 An Introduction to the Quantum Theory of Atoms in Molecules

58	L. Pauling, The Nature of the Chemical	80	K. E. Laidig, Can. J. Chem. 1996, 74,
	Bond, (Third Ed.), Cornell University		1131–1138.
	Press: Ithaca, N.Y., 1960.	81	K. M. Gough, M. M. Yacowar, R. H.
59	C. F. Matta, FRAGDIP (QCPE 0801)		Cleve, J. R. Dwyer, Can. J. Chem.
	Quantum Chemistry Program		1996, 74, 1139–1144.
	Exchange, Indiana University, 2001.	82	K. M. Gough, H. K. Srivastava,
	(http://qcpe.chem.indiana.edu/).		K. Belohorcova´, J. Chem. Phys. 1993,
60	C. F. Matta, R. F. W. Bader, Proteins:		98, 9669–9677.
	Struct. Funct. Genet. 2003, 52,	83	K. M. Gough, H. K. Srivastava,
	360–399.		K. Belohorcova´, J. Phys. Chem. 1994,
61	M. J. Frisch, et al., Gaussian 03,		98, 771–776.
	Gaussian Inc.: Pittsburgh PA, 2003.	84	K. M. Gough, H. K. Srivastava, J. Phys.
62	C. G. Gray, K. E. Gubbins, Theory of		Chem. 1996, 100, 5210–5216.
	Molecular Fluids, (Vol. 1), Clarendon	85	R. L. A. Haiduke, A. E. de Oliveira,
	Press: Oxford, 1984.		R. E. Bruns, J. Phys. Chem. A 2004,
63	E. Espinosa, E. Molins, J. Chem. Phys.		108, 6788–6796.
	2000, 113, 5686–5694.	86	J. V. da Silva, R. L. A. Haiduke, R. E.
64	O. A. Zhikol, O. Shishkin, K. A.		Bruns, J. Phys. Chem. A 2006, 110,
	Lyssenko, J. Leszczynski, J. Chem.		4839–4845.
	Phys. 2005, 122, 144104-1–144104-8.	87	P. H. Ce´sar, S. H. D. M. Faria, J. V.
65	M. P. Waller , A. Robertazzi, J. A.		da Silva Jr., R. L. A. Haiduke, R. E.
	Platts, D. E. Hibbs, P. A. Williams,		Bruns, Chem. Phys. 2005, 317, 35–
	J. Comput. Chem. 2006, 27, 491–504.		42 .
66	C. F. Matta, N. Castillo, R. J. Boyd,	88	R. L. A. Haiduke, R. E. Bruns, J. Phys.
	J. Phys. Chem. B 2006, 110, 563–578.		Chem. A 2005, 109, 2680–2688.
67	S. E. O’Brien, P. L. A. Popelier,	89	R. F. W. Bader, D. Bayles, G. L.
	Can. J. Chem. 1999, 77, 28–36.		Heard, J. Chem. Phys. 2000, 112,
68	P. L. A. Popelier, J. Phys. Chem. A		10095–10105.
	1999, 103, 2883–2890.	90	K. E. Laidig, Chem. Phys. Lett. 1991,
69	S. E. O’Brien, P. L. A. Popelier, J. Chem.		185, 483–489.
	Inf. Comput. Sci. 2001, 41, 764–775.	91	R. F. W. Bader, Mol. Phys. 2002, 100,
70	U. A. Chaudry, P. L. A. Popelier,		3333–3344.
	J. Org. Chem. 2004, 69, 233–241.	92	P. F. Zou, R. F. W. Bader, Acta Cryst.
71	R. Carbo´, L. Leyda, M. Arnau, Int. J.		A 1994, 50, 714–725.
	Quantum Chem. 1980, 17, 1185–1189.	93	R. F. W. Bader, D. Bayles, J. Phys.
72	K. B. Wiberg, R. F. W. Bader, C. D. H.		Chem. A 2000, 104, 5579–5589.
	Lau, J. Am. Chem. Soc. 1987, 109,	94	R. F. W. Bader, A. Streitwieser, A.
	1001–1012.		Neuhaus, K. E. Laidig, P. Speers,
73	T. A. Keith, R. F. W. Bader, Chem.		J. Am. Chem. Soc. 1996, 118,
	Phys. Lett. 1992, 194, 1–8.		4959–4965.
74	T. A. Keith, R. F. W. Bader, Int. J.	95	R. F. W. Bader, S. Johnson, T.-H.
	Quantum Chem. 1996, 60, 373–379.		Tang, P. L. A. Popelier, J. Phys. Chem.
75	R. F. W. Bader, T. A. Keith, J. Chem.		1996, 100, 15398–15415.
	Phys. 1993, 99, 3683–3693.	96	K. R. Adam, J. Phys. Chem. A 2002,
76	T. A. Keith, R. F. W. Bader, Chem.		106, 11963–11972.
	Phys. Lett. 1993, 210, 223–231.	97	M. Song, C. M. Breneman, J. Bi, N.
77	T. A. Keith, R. F. W. Bader, J. Chem.		Sukumar, K. P. Bennett, S. Cramer,
	Phys. 1993, 99, 3669–3682.		N. Tugcu, J. Chem. Inf. Comput. Sci.
78	R. F. W. Bader, M. T. Carroll, J. R.		2002, 42, 1347–1357.
	Cheeseman, C. Chang, J. Am. Chem.	98	C. M. Breneman, M. Rhem,
	Soc. 1987, 109, 7968–7979.		J. Comput. Chem. 1997, 18, 182–197.
79	R. F. W. Bader, T. A. Keith, K. M.	99	C. F. Matta, J. Herna´ndez-Trujillo,
	Gough, K. E. Laidig, Mol. Phys. 1992,		R. F. W. Bader, J. Phys. Chem. A 2002,
	75, 1167–1189.		106, 7369–7375.

			References	33
100	N. Castillo, C. F. Matta, R. J. Boyd,	117	C. F. Matta, J. Phys. Chem. A 2001,
	J. Chem. Inf. Mod. 2005, 45, 354–		105, 11088–11101.
	359.	118	B. Dittrich, T. Koritsa´nszky,
101	S. Y. Liem, P. L. A. Popelier, J. Chem.		M. Grosche, W. Scherer, R. Flaig,
	Phys. 2003, 119, 4560–4566.		A. Wagner, H. G. Krane, H. Kessler,
102	H. J. Boho´rquez, M. Obrego´n, C.		C. Riemer, A. M. M. Schreurs,
	Ca´rdenas, E. Llanos, C. Sua´rez, J. L.		P. Luger, Acta Cryst. B 2002, 58,
	Villaveces, M. E. Patarroyo, J. Phys.		721–727.
	Chem. A. 2003, 107, 10090–10097.	119	S. Scheins, M. Messerschmidt,
103	P. L. A. Popelier, F. M. Aicken,		P. Luger, Acta Cryst. B 2005, 61,
	ChemPysChem 2003, 4, 824–829.		443–448.
104	P. L. A. Popelier, F. M. Aicken, J. Am.	120	D. S. Kosov, P. L. A. Popelier, J. Chem.
	Chem. Soc. 2003, 125, 1284–1292.		Phys. 2000, 113, 3969–3974.
105	C. Chang, R. F. W. Bader, J. Phys.	121	D. S. Kosov, P. L. A. Popelier, J. Phys.
	Chem. 1992, 96, 1654–1662.		Chem. A 2000, 104, 7339–7345.
106	C. M. Breneman, T. R. Thompson,	122	P. L. A. Popelier, L. Joubert, D. S.
	M. Rhem, M. Dung, Comput. Chem.		Kosov, J. Phys. Chem. A 2001, 105,
	1995, 19, 161–179.		8254–8261.
107	C. M. Breneman, L. W. Weber, in: The	123	J. A. Platts, Phys. Chem. Chem. Phys.
	application of charge density research to		2000, 2, 973–980.
	chemistry and drug design (NATO ASI	124	J. A. Platts, Phys. Chem. Chem. Phys.
	Series), (G. A. Je rey, J. F. E. Piniella,		2000, 2, 3115–3120.
	Eds.) Plenum Press, New York, 1991,	125	T. Dumitrica, C. M. Landis, B. I.
	pp 357–358.		Yakobson, Chem. Phys. Lett. 2002,
108	C. F. Matta, R. F. W. Bader, Proteins:		360, 182–188.
	Struct. Funct. Genet. 2000, 40,	126	T. S. Koritsanszky, P. Coppens, Chem.
	310–329.		Rev. 2001, 101, 1583–1628.
109	C. F. Matta, R. F. W. Bader, Proteins:	127	W. Koch, M. C. Holthausen,
	Struct. Funct. Genet. 2002, 48,		A Chemist’s Guide to Density
	519–538.		Functional Theory, (Second Edition),
110	R. F. W. Bader, F. J. Martı´n, Can. J.		Wiley–VCH: New York, 2001.
	Chem. 1998, 76, 284–291.	128	M. W. Schmidt, K. K. Baldridge, J. A.
111	F. J. Martı´n, Theoretical Synthesis of		Boatz, S. T. Elbert, M. S. Gordon, J. H.
	Macromolecules from Transferable		Jensen, S. Koseki, N. Matsunaga, K. A.
	Functional Groups, Ph.D. Thesis,		Nguyen, S. J. Su, T. L. Windus,
	McMaster University: Hamilton,		M. Dupuis, J. A. Montgomery,
	2001.		J. Comput. Chem. 1993, 14,
112	R. F. W. Bader, C. F. Matta, F. J.		1347–1363.
	Martı´n, Chapter 7 in: Medicinal	129	Bader, R. F. W., http://
	Quantum Chemistry, (F. Alber,		www.chemistry.mcmaster.ca/aimpac/.
	P. Carloni, Eds.) Wiley–VCH:	130	F. W. Biegler-Ko¨nig, T. T. Nguyen-
	Weinheim, 2003, pp 201–231.		Dang, Y. Tal, R. F. W. Bader, A. J.
113	V. Pichon-Pesme, C. Lecomte, R.		Duke J. Phys. B: At. Mol. Phys. 1981,
	Wiest, M. Be´nard, J. Am. Chem. Soc.		14, 2739–2751.
	1992, 114, 2713–2715.	131	F. W. Biegler-Ko¨nig, R. F. W. Bader,
114	R. Wiest, V. Pichon-Pesme, M.		T.-H. Tang, J. Comput. Chem. 1982,
	Be´nard, C. Lecomte J. Phys. Chem.		13, 317–328.
	1994, 98, 1351–1362.	132	Popelier, P. L. A., MORPHY, UMIST,
115	V. Pichon-Pesme, C. Lecomte,		England, EU, 1998.
	H. Lachekar, J. Phys. Chem. 1995, 99,	133	F. W. Biegler-Ko¨nig, J. Scho¨nbohm,
	6242–6250.		D. Bayles, J. Comput. Chem. 2001, 22,
116	C. Jelsch, V. Pichon-Pesme,		545–559.
	C. Lecomte, A. Aubry, Acta Cryst. D	134	F. W. Biegler-Ko¨nig, J. Comput. Chem.
	1998, 54, 1306–1318.		2000, 21, 1040–1048.

34 1 An Introduction to the Quantum Theory of Atoms in Molecules

135	F. W. Biegler-Ko¨nig, J. Scho¨nbohm,	140	J. A. Platts, CCL: MP2 virial value (8
	D. Bayles, AIM2000 Website: http://		July 2005), http://www.ccl.net/cgi-bin/
	gauss.fh-bielefeld.de/aim2000.		ccl/message.cgi?2005+07+08+004.
136	C. Gatti, TOPOND, CNR-CSRSRC:	141	F. Corte´s-Guzma´n, R. F. W. Bader,
	Milano, 1998.		Chem. Phys. Lett. 2003, 379, 183–
137	V. R. Saunders, R. Dovesi, C. Roetti,		192.
	R. Orlando, C. M. Zicovich-Wilson,	142	T. A. Keith, Link for self-consistent
	N. M. Harrison, K. Doll, B. Civalleri,		virial scaling (SCVS) in Gaussian 94/
	I. J. Bush, Ph. D’Arco, M. Llunell,		98, 1998.
	CRYSTAL 2003.	143	P.-O. Lo¨wdin, J. Mol. Spectr. 1959, 3,
138	Surfer 08, Golden Software, Inc.,		46–66.
	Golden, Colorado, USA, 2002.	144	D. E. Magnoli, J. R. Murdoch, Int. J.
139	T. A. Keith, AIMALL97 for Windows,		Quantum Chem. 1982, 22, 1249–
	1997.		1262.

Part I

Advances in Theory

37

2

The Lagrangian Approach to Chemistry

Richard F. W. Bader

2.1 Introduction

This article is written by a chemist for other chemists to explain how and why the definition of an atom in a molecule requires that one foregoes the usual Hamiltonian approach to quantum mechanics and replace it with one expressed in terms of the Lagrangian and the associated action principle. A consequence of the Lagrangian approach to chemistry is the possibility of foregoing arbitrary models and dealing instead with observation and physics, so the article should be of particular interest to experimentalists. It is addressed in particular to younger chemists, those willing to extend their knowledge of quantum mechanics beyond the orbital model of electronic structure.

2.1.1

From Observation, to Physics, to QTAIM

Thirty-four years have passed since it was first postulated that the virial theorem should apply to a bounded region of real space – to an atom in a molecule [1]. This postulate was put forth on the basis of the observation of the paralleling transferability of the topological properties of the electron and kinetic energy densities. In another three years, bringing one to 1975, this postulate was derived starting from Schro¨dinger’s first paper on ‘‘wave mechanics’’ [2]. The 1975 paper, by yielding a variational derivation of the virial theorem for an atom in a molecule, was the initial step in establishing a variational definition of ‘‘an atom in a molecule’’, one derived from the Lagrangian approach to physics. Thus one proceeded from observation, to physics, to the quantum theory of atoms in molecules, QTAIM, a theory that applies equally to the total system and to its constituent atoms [3]. By building upon Schwinger’s principle of stationary action [4] that follows the Lagrangian approach to physics, QTAIM yields a variational statement of the Heisenberg equation of motion for all quantum observables and establishes the equal applicability of these equations to the total system and its con-

38 2 The Lagrangian Approach to Chemistry

stituent atoms. In the Heisenberg approach, quantum mechanics is represented in terms of the equations of motion of the observables, thus emphasizing the ties that link theory to observation. Thus QTAIM, by uniting the Heisenberg and Lagrangian approaches to physics, unites theoretical chemistry with experiment.

QTAIM brings to the fore the modus operandi of quantum mechanics – to use the equations of motion – the theorems of quantum mechanics – to predict and understand the observed properties of a system. This is the approach followed by Slater in his use of the virial and Feynman theorems which he considered to be ‘‘two of the most powerful theorems applicable to molecules and solids’’ [5]. QTAIM, by extending these and all theorems to an atom in a molecule, enables one to apply this approach to all problems at the atomic level. The time has arrived to replace the criticisms of these powerful theorems that one finds throughout the literature, with the clarity and predictive powers of physics.

2.2

The Lagrangian Approach

2.2.1

What is The Lagrangian Approach and What Does it Do?

The Hamiltonian approach to quantum mechanics evolved from Schro¨dinger’s wave equation that he derived in 1926 [6]. Yourgrau and Mandelstam (Y&M) in their prelude to introducing the Lagrangian approach in their monograph on variational principles in quantum theory state: ‘‘The ordinary Hamiltonian presentation of quantum mechanics contains, apart from the basic principles of the subject, two distinct postulates: the commutation relations between generalized co-ordinates and the momenta, and the equations of motion’’ [7]. The alternative ‘‘Lagrangian approach’’, is based on the action principle, which in its earliest form was referred to as the principle of least action – first enunciated somewhat imperfectly by Maupertuis in 1744 and stated in its present form by Hamilton in 1834. Y&M point out that in classical mechanics the Lagrangian formalism can be substituted for the Hamilton theory enabling the laws of mechanics to be expressed as a single postulate, the principle of least action stated by Hamilton. Y&M go on to ask: ‘‘The obvious question that arises from such considerations: is it not possible, and moreover most desirable, to obtain a similar Lagrangian formulation of the quantum laws depending upon a single postulate only? This aim is achieved by the Feynman and Schwinger theories’’ [7]. Their theories re-introduced the action principle into the active fabric of physics, Feynman [8] in 1948 and Schwinger [4] in 1951, and yield both the equations of motion and the commutation relations. This chapter shows how Schwinger’s formulation enables one to ask and answer the question ‘‘what is an atom in a molecule?’’, a question that cannot be posed within the Hamiltonian approach. Answering the question takes one on an intellectual journey beginning with Schro¨dinger, on to Dirac, and end-

2.2 The Lagrangian Approach 39

ing with Schwinger, whose principle of stationary action can be extended to yield the physics of an open system and thus, the theory of atoms in molecules [3]. The work of Feynman and Schwinger may provide ‘‘the real foundation of quantum mechanics’’ [9]. Its extension to an atom in a molecule will bring to bear the advantages of this approach to the understanding and prediction of chemistry [10].

The derivation of the atomistic approach from the action principle imparts the certainty of physics to the molecular structure hypothesis – that a molecule is a collection of atoms with additive, characteristic properties linked by a network of bonds that impart a structure – a concept forged in the crucible of nineteenthcentury experimental chemistry. One hundred and fifty years of experimental chemistry underlie the realization that the properties of a total system are the sum of its atomic contributions and Dalton’s atomic hypothesis has emerged as the operational theory of chemistry. The time has arrived for a shift of emphasis in the prediction and understanding of chemistry, away from a philosophy based on the premise held by some that because chemical concepts are beyond physics, one is free to formulate and choose between a plethora of frequently conflicting subjective models.

This chapter is intended for a wide audience. Each section opens with an introduction to the essential underlying ideas and their reading will take one through to the chapter’s goal – an understanding of the rooting of the atomic concept in the fabric of quantum mechanics. Experimental chemists with a limited knowledge of physics, such as I when I first switched to theory, may skip intervening sections that provide those more knowledgeable of physics with more mathematical detail. A recent article provides a narrative of the development of the theory of atoms in molecules from the properties of the measurable electron density distribution [11].

2.2.2

The Lagrangian and the Action Principle – A Return to the Beginnings

It was the classical concept of ‘‘action’’ that provided Schro¨dinger with the con-

^ ¼

ceptual basis for his derivation of Hc Ec in the first of the four papers on ‘‘wave mechanics’’ that he published in 1926 [6]. He based its derivation on an analogy with a method of obtaining a solution to the classical equations of motion that corresponds to finding the time integral of the Lagrangian over the motion in question, the ‘‘action integral’’. Thus the action provided the starting point for Schro¨dinger’s derivation of his equation that evolved into the Hamiltonian approach to quantum mechanics. The quantum theory of an atom in a molecule (QTAIM) was, in turn, first obtained by extension of Schro¨dinger’s derivation to a system with finite boundaries [2]. Thus the initial step on the path that leads to the development an atom in a molecule is accomplished by a return to the action at the beginning of quantum mechanics, a path that leads directly to Schwinger’s principle of stationary action [4]. It is the purpose of this section to demonstrate that wave mechanics had its origin in the action principle and to show

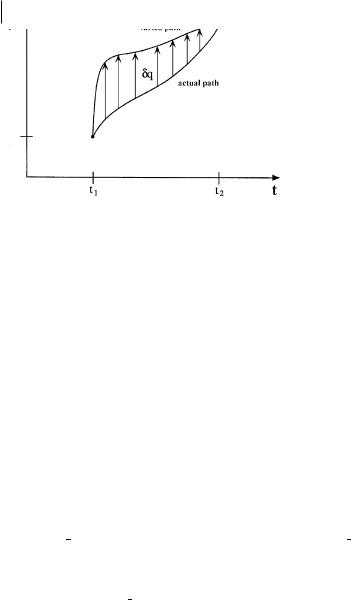
40 2 The Lagrangian Approach to Chemistry

Fig. 2.1 A representation of the actual path and a possible varied path obtained by variation of the position coordinate q connecting the initial (q1, t1) and final (q2, t2) space–time points for a classical system.

how this leads unavoidably to the definition of an atom as a bounded piece of real space.

2.2.3

Minimization of the Action

The principle of least action states that a quantity called the action is minimized as a system moves from one configuration to another – the action is said to be ‘‘stationary’’ relative to variations in the space–time path connecting the two configurations. Such a path is depicted in Fig. 2.1 for a classical trajectory connecting initial and final points in space; q1 and q2, at the corresponding times t1 and t2.

The action, denoted by W12, with the dimensions of Planck’s constant h (energy time) is the time integral between the limits t1 and t2, of the Lagrangian Lðq; q; tÞ, a function of the coordinates q, their velocities q and the time t (Eq. 1):

W12	¼	ðt1	Lðq; q; tÞ dt	ð1Þ
		t2

The mathematical procedure used to minimize the action over an entire path is outlined below for those desirous of a more complete description. The procedure yields a di erential equation, the Euler equation, the equation of motion for the chosen Lagrangian; the classical action integral yielding Lagrange’s equations and the quantum action yielding Schro¨dinger’s equation. Thus the action principle enables one to derive Newton’s and Schro¨dinger’s equations and in this sense alone it is a more fundamental statement of physics.

2.2 The Lagrangian Approach 41

2.2.4

Steps in Minimizing the Action

The classical Lagrangian equals the di erence between the kinetic and potential energies, L ¼ T V. It has a value at each point on the trajectory and the ‘‘sum’’ of these values between the two time limits must be a minimum. This problem is distinct from finding an extremum in some function at a single point in space using di erential calculus. Determining an extremum of a function over an entire path is accomplished using the ‘‘calculus of variations’’. Assuming the existence of the ‘‘actual path’’ that is to be found, one generates a ‘‘varied path’’ coterminus in space and time, by displacing q on the actual path by an amount dq at each time t, as depicted in Fig. 2.1, thereby causing a variation or first-order change in the action integral, dW12. Because W12 must be a minimum for the true path, the variation dW12 must vanish, and the action is said to be ‘‘stationary’’. One of Feynman’s lectures [12] presents a clear and very readable presentation of the elementary mathematics underlying the derivation of the expression for dW12 ¼ 0.

The mathematical result of varying the action integral is shown in Eq. (2) for a single coordinate q.

dW12	¼	ðt1 fðqL=qqÞ dðqL=qqÞ=dtgdq dt ¼ 0	ð2Þ
		t2

The variations in q are re-expressed in terms of dq using an integration by parts (refer to Feynman’s lecture) and the resulting terms at the time end points are discarded. Thus, the result of the variation is given by the group of terms enclosed in the curly brackets in Eq. (2), all multiplied only by dq, the variations in q. Because dq is arbitrary, the only way in which the variation dW12 can vanish is for the group of terms in the curly brackets to equal zero, yielding a di erential equation, representing Lagrange’s equations:

qL=qq dðqL=qqÞ=dt ¼ 0 ð3Þ

This, as pointed out above, is a general result – minimizing the action generates a di erential equation, called the Euler equation that for the classical action is Lagrange’s equation of motion. For a single particle L ¼ mq2=2 VðqÞ and the equation reduces to Newton’s equation of motion, i.e. the force, given byqV=qq, equals mass times acceleration, mq€.

If one employs the quantum mechanical Lagrangian and causes the action to be stationary relative to first-order variations in the wave function C, one obtains

Schrodinger’s¨	^
	time dependent equation, ihqC=qt ¼ HC, as the Euler equation.

Because Cðq; tÞ is a function of the coordinates and time, one must perform the variations over the whole of configuration space – all values of q – between the two time limits, a procedure that again clearly requires the methods of the calculus of variations.