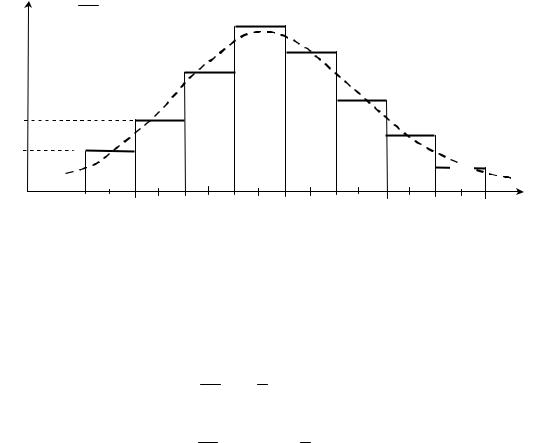
Графическое изображение статистического ряда – это гистограмма.

Рисуем оси координат, делаем разметку осей, наносим на ось Х границы

интервалов и их середины. После этого строим на каждом отрезке прямоуголь-

ники высотой i . Аппроксимируем фигуру из прямоугольников пунктирной

линией (рис. 8.1). По виду этой кривой можно выдвинуть предположение (ги-

потезу) о

виде

закона

распределения

генеральной

случайной

величиной X

(на рис. 8.1. видно, что пунктирная линия похожа на кривую Гаусса, которая

относится к нормальному закону).

i

mi

Р

n

И

2

У

1

Г x0k

x01

x02

x0i

a

1

b

ai

bi

Б a

k

b

k

X

1

а

xmin

xmax

Риск. 8.1

Имея статистический ряд можноеоценить числовые характеристики гене-

ральной случайной величин й X :

k

m

i

1

i

i

M[x]

т

mix0

a,

n

x0

n

i 1

о

и

k

mi

i

a)

2

1

i

a)

2

л

D[x]

i 1 n

(x0

n mi (x0

.

б

8.2. Оценки и методы их получения

и

Приближенные значения параметров, входящих в законы распределения,

Б

определяемые каким-либо способом по выборкам, называются оценками или

статистиками. Оценки бывают точечными и интервальными. Точечные оцен-

ки представляются одним числом, интервальные – двумя числами ( 1 и 2) :

началом и концом интервала, накрывающего оцениваемый параметр. Самыми

распространенными методами получения точечных оценок являются метод

моментов и метод наибольшего правдоподобия.

104

8.2.1. Метод моментов

Пусть генеральная случайная величина Х имеет плотность распределения f(х). Начальный и центральный моменты можно найти так (см. раздел 4.1.6):

K

xk f (x)dx,

(8.1)

K

(x 1)k f (x)dx.

(8.2)

По выборке x1,x2,...,xn определяем выборочные начальные и центральные

моменты:

Р

1

n

K

И

K

xi

,

(8.3)

У

n i 1

1

n

K

i 1

(xi

1)K .

Г

(8.4)

n

Метод моментов состоит в том, что генер льные моменты (8.1, 8.2), в ко-

Б

торые входят оцениваемые параметры, приблизительно приравниваются к со-

ответствующим выборочным

(8.3), (8.4). Составляется система урав-

нений:

а

к

k

k ,

(8.5)

моментам

(8.6)

k

k .

Решая систему (8.5), (8.6), находим оцениваемые параметры.

т

Особо важную

играет

– выборочный начальный момент 1-го по-

роль

1

рядка, он называется выборочным средним и обозначается

:

x

и

л

1

n

x

xi .

(8.7)

б

n i 1

Следующим по важности выборочным моментом является выборочный

центральныйи момент 2-го порядка

, который называется выборочной дис-

2

персией и обозначается S2

:

Б

S2 1 n (xi x)2 . n i 1

Наиболее часто используются две формулы метода моментов.

M[X] x,

(8.8)

(8.9)

105

D[X] S2 .	(8.10)
Сформулируем метод моментов в общем виде.

Пусть f (x, 1, 2,..., r ) плотность распределения случайной величины

Х, где i – неизвестные параметры. Чтобы найти оценки 1, 2,..., r , выра-

жаем первые r начальных или центральных моментов случайной величины Х через параметры 1, 2,..., r , затем генеральные моменты аппроксимируем соответствующими выборочными. В результате имеем систему из r уравне-

ний с r неизвестными, откуда и получаем 1, 2,..., r .

Пример.

Пусть генеральная случайная величина Х имеет показательный закон рас-

пределения с плотностью

f (x) e x , x 0,

0. По выборке x ,x ,...,x ме-

тодом моментов найти оценку параметра .

У

1

Р2 n

И

1. Определяем 1 , используя (8.1):

u x, dv e xdx,

1 =M X = x e xdx

xe xdx

Б

du dxГ, v

1

e

x

0

0

а

= 1e xx

e x

к

1 .

2

0

е1

0

2. По (8.3) или (8.7) находим выборочный начальный момент 1-го поряд-

ка или

и составляем выражение вида (8.5) или (8.9):

x

о

x.

и

1

3. Заменяя в п. 2

на

тценку

, составим уравнение:

x.

л

4. Откуда опреде

м оценку параметра

:

б

1

1

.

и

1 n

x

xi

Б

n i 1

8.2.2. Метод наибольшего правдоподобия

Этот метод предложен математиком Фишером в 1912 г.

Пусть f (x, 1, 2,..., r ) – плотность распределения генеральной случайной величины Х, где 1, 2,..., r – неизвестные параметры. Согласно методу,

наилучшими оценками ˆ1,ˆ2,...,ˆr параметров 1, 2,..., r являются такие, для которых функция правдоподобия L принимает наибольшее значение.

106

Для непрерывной случайной величины

n
L( 1,..., r ,x1,...,xn) f (xi, 1,..., r ).	(8.11)
i 1
Для дискретной случайной величины
n
L( 1,..., r ,x1,...,xn) P(xi, 1,..., r ).	(8.12)
i 1
Здесь x1,x2,...,xn – выборка из генеральной случайной величины Х.

Априорные выборочные значения x1,x2,...,xn – являются независимымиР случайными величинами, закон распределения которых совпадает с законом

распределения генеральной случайной величины Х. Тогда правуюИчасть (8.11) на основании теоремы умножения законов распределений (см. раздел 3.5) мож-

но рассматривать как плотность распределения вероятности n-мерного вектора

У

случайный

(X1, X2, …, Xn). Согласно методу, для наилучших оценок ˆ

,ˆ

,...,ˆ

r

Г

1

2

вектор (X1, X2, …, Xn) будет иметь наибольшую плотность распределения. То

есть надо найти такие оценки ˆ

,ˆ

,...,ˆ

, для которых функция правдоподобия

1

2

r

Б

L – максимальна. Для этого составляют и реш ют такую систему уравнений:

L

а

0, (i

1,r).

(8.13)

i

к

Так как функция и ее логарифмедостигают экстремума в одной точке, то

часто для упрощения решения задачи используют логарифмическую функцию

правдоподобия. В случае л гарифмической функции правдоподобия составля-
ется система следующ х уравненийт:
				о
			и		lnL	0, (i		).		(8.14)
							1,r
					i
		л
Пр мер.
Пусть генеральная случайная величина Х имеет показательный закон рас-
	б								0 .	По выборке x ,x ,...,x
пределен я с плотностью f (x, ) e x , x 0 ,
и										1 2	n
методом наибольшего правдоподобия найти оценку параметра .
1. Так как нам необходимо оценить один параметр , то надо составить и
Б
решить одно уравнение. Найдем функцию правдоподобия, используя (8.11):
										n
				n		n			n	xi
	L( ,x1,...,xn) f (xi, )= e xi n e xi ne i 1 .
				i 1		i 1			i 1

107