Если из трех главных значений тензоров совпадают два, то кристалл относится к одноосным (кристаллы ромбоэдрической, тетрагональной и гексагональной систем). Одна из главных осей – оптическая ось кристалла

– совпадает с осью поворота на угол 2π / n , n = 3, 4, 6; соответствующие главные значения обозначаются как ε и µ . Две другие главные оси,

перпендикулярные между собой, расположены произвольно в плоскости, перпендикулярной оптической оси; главные значения для них обозначают через ε и µ . Тогда при выборе оптической оси вдоль z

ε		0	0					µ		0	0
	0	ε	0			,	µˆ		0	µ	0		(2.6.13)
εˆ =								=				.
	0	0	ε						0	0	µ

Наконец, при различии всех трех главных значений тензоров (кристаллы триклинной, моноклинной и ромбической систем) говорят о двухосных кристаллах. Заметим, что положение всех трех главных осей фиксировано кристаллографическими направлениями только в кристаллах ромбической системы. Для других же систем эти направления (все три для триклинной системы и два для моноклинной системы) зависят от частоты; в этих случаях направления главных осей для вещественных и мнимых частей тензоров εˆ и µˆ могут различаться, так что одновременно они не

будут приводиться к диагональному виду. Однако в областях оптической прозрачности мнимые части тензоров пренебрежимо малы, а для естественных оптических сред магнитная проницаемость близка к единице, так что основное значение имеет тензор вещественной части диэлектрической проницаемости.

2.6.2. Нелинейные восприимчивости

Общие соотношения

Будем считать здесь среду однородной, стационарной. Для простоты ограничимся случаем среды с магнитной проницаемостью µ =1 , не

обладающей пространственной дисперсией. Как и в (2.4.1) разлагаем поляризованность в ряд по степеням амплитуды излучения

P = P(1) +ξP(2) +ξ2P(3) +... .

(2.6.14)

Естественным обобщением линейного соотношения (3) для поляризованности служат следующие интегральные представления (общее ввиду отсутствия пространственной дисперсии значение координаты r опускаем):

87

		3	∞	∞
Pi	(2) (t) = ∑		∫dτ1 ∫dτ2			χi(2), j1 j2 (τ1,τ2 )E j1 (t −τ1 )E j2 (t −τ2 ),
		j1, j2 =1	0	0
		3		∞	∞	∞
Pi	(3) (t) =	∑		∫dτ1	∫dτ2 ∫dτ3 χi(3), j1 j2 j3 (τ1,τ2 ,τ3 )E j1 (t −τ1 )E j2 (t −τ2 )E j3 (t −τ3 ),
		j1, j2 , j3=1		0	0	0
...
		3		∞	∞
Pi(k ) (t) =		∑		∫dτ1...∫dτk			χi(,kj1)... jk (τ1,...,τk )E j1 (t −τ1 )...E jk (t −τk ).
		j1,..., jk =1		0	0		(2.6.15)
При k = 1 определяемая							(15) линейная поляризованность совпадает в

указанных предположениях с выражением (3). Вообще говоря, наряду с

электрической		напряженностью	под интегралом	в	(15) могут
фигурировать		и напряженности	магнитного поля		, например
				H
E j	(t −τ1 )H j (t −τ2 ) при k = 2. Однако в большинстве задач их можно не
1	2

включать в разложение (15). Дело в том, что электрические и магнитные компоненты оптического излучения не независимы, а связаны уравнениями Максвелла, в частности, так как само разложение (14)

предполагает малость нелинейности, по порядку величины E и H

			ε0
совпадают (	H	≈	µ0		E		, где ε0	и µ0 – линейные диэлектрическая и

магнитная проницаемости). Поэтому для дополнения (15) членами с напряженностями магнитного поля нет физических оснований. Напомним,

однако, что в наших обозначениях E и H быстро, с оптическими частотами, осциллируют. Поэтому здесь не идет речь об эффектах типа электрооптических или магнитооптических; для описания последних включение в разложения (15) напряженностей статических или низкочастотных магнитных полей вполне оправдано.

Будем считать, что излучение состоит из набора монохроматических полей, см. (2.3.83). Соответственно, поляризованность k-го порядка имеет вид (2.4.3) и (2.4.30), причем развернутая форма записи (2.4.30) следующая:

Pi(k ) (ωf1 ,ωf2 ,...,ωfk ) =

= ∑ χi(,kj1),..., jk (ωf1 +ωf2 +... +ωfk ;ωf1 ,ωf2 ,...,ωf3 )E j1 (ωf1 )E j2 (ωf2 )...E jk (ωfk ).

j1,..., jk

(2.6.16)

Из сравнения (16) с (15) находим связь нелинейных восприимчивостей χi(,kj1),..., jk (ωf1 +... +ωfk ;ωf1 ,...,ωfk ) с функциями отклика χi(,kj1)... jk (τ1,...,τk ) :

88

χi(,kj1),..., jk (ωf1 +... +ωfk ;ωf1 ,...,ωfk ) =

∞

∞

(2.6.17)

= ∫dτ1...∫dτk χi(,kj1)... jk (τ1,...,τk )exp[i(ωf1τ1 +... +ωfkτk )].

0 0

Отметим здесь некоторые общие свойства тензоров нелинейной восприимчивости. Непосредственно из (16) следует перестановочная симметрия: можно менять местами любую пару частотных аргументов вместе с соответствующим декартовым индексом, например

χi(,kj), j	..., j	(ωf		+ωf	+... +ωf ;ωf			,ωf	,...,ωf	) =	(2.6.18)
1 2	k		1		2		k 1	2	k
= χi(,kj)		, j	..., j	(ωf	+ωf	2	+... +ωf	;ωf	,ωf ,...,ωf ).
	2	1	k	1			k		2 1	k

Вещественность функций отклика приводит к тому, что изменение знаков всех частот эквивалентно комплексному сопряжению восприимчивости:

χi(,kj1),..., jk (−ωf1 −... −ωfk ;−ωf1 ,...,−ωfk ) = χi(,kj1)*,..., jk (ωf1 +... +ωfk ;ωf1 ,...,ωfk ) . (2.6.19)

Как уже упоминалось, связь между вещественными и мнимыми частями восприимчивости среды, находящейся в отсутствие излучения в термодинамическом равновесии, также определяется соотношениями типа Крамерса – Кронига.

В областях прозрачности нелинейные проницаемости вещественны (что следует из рассмотрения микромоделей с помощью матрицы плотности в отсутствии релаксации, γnm = 0 ). При этом возникает

дополнительная симметрия тензоров восприимчивости по индексам, включающая перестановки первого индекса. Эту симметрию нам будет удобней обсудить в следующих главах. Здесь же мы отметим играющую особую роль пространственную симметрию аморфных и кристаллических тел. Точнее, имеется в виду симметрия в расположении частиц среды – атомов, ионов и молекул – при статистическом усреднении их положений, флуктуирующем при тепловом движении. Фактор пространственной симметрии был важен и в линейной области при разделении сред на оптические изотропные и одноосные и двухосные кристаллы. Но применительно к феноменологическим нелинейным восприимчивостям этот фактор особенно актуален, так как его использование позволяет резко сократить число ненулевых и различающихся компонент восприимчивостей.

Пространственная симметрия кристаллов

Здесь мы представим только краткое изложение этого вопроса, отсылая читателя за подробностями, например, к монографии [37]. Под симметрией идеальных кристаллов понимается свойство совмещения

89

решетки составляющих их частиц при параллельных переносах, поворотах, отражениях или части или комбинации этих операций.

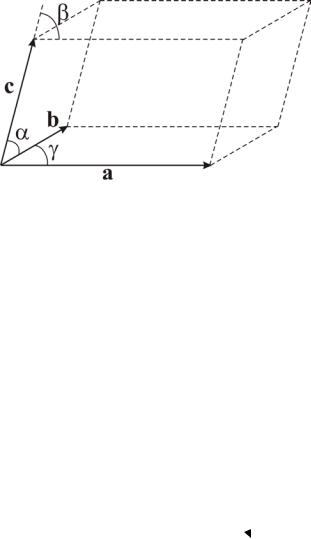
Основное свойство идеального кристалла заключается в возможности выделения в нем такой элементарной ячейки (параллелепипед, рис. 2.9) с фиксированным расположением частиц в ней, что параллельный перенос ячейки на вектор трансляции также дает элементарную ячейку и применение к элементарной ячейке всех операций трансляции покрывает все пространство. Формирующие кристаллическую решетку частицы не обязательно находятся в узлах элементарной решетки; в частном случае такого совпадения говорят о примитивной ячейке, узлы которой представляют все точки решетки. Для элементарных ячеек приняты следующие обозначения, указывающие на характер расположения частиц в ячейке:

P – примитивная ячейка (в том числе R – ромбоэдр); C – с центрированными основаниями;

I – объемноцентрированная ячейка;

F – гранецентрированная ячейка.

Вектора трансляции Т связаны с векторами, построенными на ребрах элементарной решетки a, b и c (см. рис. 2.9), соотношением

T = ia + jb + kc ,	(2.6.20)
где i, j и k – целые числа.

Рис. 2.9. Элементарная ячейка кристалла в виде параллелепипеда с ребрами a, b и c и углами между ними α, β и γ.

В зависимости от соотношений между длинами ребер элементарной ячейки и углами между ними имеется 7 кристаллических систем, см. Табл. 2.1.

Таблица 2.1. Кристаллические системы

Кристаллическая	система	Соотношение	Соотношение углов
(типы ячеек)		длин ребер
Триклинная (Р)		a ≠ b ≠ c	α ≠ β ≠γ
Моноклинная (P, C)		a ≠ b ≠ c	α =γ =π / 2 ≠ β

90

Ромбическая (P, C, I, F)		a ≠ b ≠ c		α = β =γ =π / 2
Тетрагональная (P, I)		a = b ≠ c		α = β =γ =π / 2
Тригональная (R)		a = b = c		α = β =γ < 2π / 3, ≠π / 2
Гексагональная (Р)		a = b ≠ c		α = β =π / 2, γ = 2π / 3
Кубическая (P, I, F)		a = b = c		α = β =γ =π / 2
При исключении	трансляций сохраняется			симметрия точечных

групп (с наличием неподвижных при операциях симметрии точек), элементами которой служат:

Оси поворота на угол 2π / n , n = 1, 2, 3, 4, 6 (случай n = 1 отвечает тождественному преобразованию).

Плоскости зеркального отражения, проходящие через точки решетки.

Центр симметрии (инверсия) с совпадением кристаллической структуры при инверсии координат r → −r .

Инверсионно-поворотные оси, когда кристаллическая структура совпадает с исходной после поворота вокруг оси и последующей инверсии.

При операциях симметрии точечных групп кристаллов – поворотах и отражениях – все физические величины (скаляры, векторы и тензоры различного ранга) преобразуются так, что их новые значения равны линейным комбинациям прежних значений с коэффициентами преобразования, определяемыми углами поворота и видом и числом отражений. Естественно, что скаляры при преобразованиях не меняются. Полярные векторы (см. п. 1.2), которые можно трактовать как тензоры первого ранга, при инверсии координат меняют знак. Поэтому при

инверсии	r → −r компоненты напряженности				электрического поля и
поляризованности (обе величины – полярные векторы) меняют знаки:
Ei → −Ei ,	Pi → −Pi .					(2.6.21)
Тензоры	восприимчивости k-го	порядка	χi(,kj),..., j		, число	координатных
			1	k
индексов	у компонент которых	равно	k + 1,		обладают	рангом k + 1.

Поэтому при инверсии компоненты этих тензоров в общем случае меняются следующим образом:

χi(,kj),..., j		→ (−1)k+1 χi(,kj),..., j .		(2.6.22)
1	k	1	k

Если кристалл обладает симметрией по отношению к инверсии, то его компоненты не должны меняться при этой операции, то есть для них компоненты тензора в левой и правой частях (22) должны совпадать

χi(,kj),..., j		= (−1)k+1 χi(,kj),..., j .		(2.6.23)
1	k	1	k

Отсюда следует, что для сред с центром инверсии (они называются центросимметричными) все восприимчивости четных порядков равны нулю:

91