уравнения (из-за включения членов с производными высших порядков с малыми коэффициентами) может приводить к нефизическим решениям, исключение которых требует применения так называемой сингулярной теории возмущений (см., например, [17]).

В основе квазиоптического уравнения лежит предположение о близости поля к плоской монохроматической волне с огибающей, которая, соответственно, медленно меняется при изменении времени и пространственных координат. В некоторых случаях удобно ослабить эти условия, ограничившись требованием медленности только временного изменения огибающей. Тогда вместо (1) следует записать

E = Re{Eexp(−iω0t)} и пренебрегать при преобразовании волнового

уравнения (1.4.6) только членом ∂2E/ ∂t2 . Соответственно, в управляющем

уравнении сохранится член ∂2E/ ∂z2 . Такой подход будет проиллюстрирован в следующей части Пособия.

Формулировка закона сохранения энергии в рамках квазиоптического подхода зависит от вида нелинейности и будет конкретизирована далее. Вид потока энергии приводится в следующей задаче.

Задание 1.1. Вывести вид среднего за оптический период потока энергии (вектора Пойнтинга) излучения с линейной поляризацией в квазиоптическом приближении.

Ответ. Поскольку излучение близко к плоской волне, то поток энергии направлен преимущественно вдоль той же оси z,

< Sz >=		c		| E |2 .			(1.5.25)
	4π
Для поперечных компонент усредненного вектора Пойнтинга
< S >=		c		Im(E* E) =	c	| E |2 Φ.	(1.5.26)
		8π			8π

Здесь поле представлено в форме E =| E | exp(iΦ)ex , так что Ф – фаза излучения.

1.6. Квазиоптическое уравнение для анизотропных сред

Рассматриваем немагнитную среду ( B = H ). Исходным служит уравнение (1.5.4), поперечную проекцию которого мы перепишем в виде

2

1

2

(l)

2

∂

E

∂

D

4π ∂ δP

∂Ez

= 0. (1.6.1)

∆ E

+

∂z2

−

c2

∂t2

−

c2 ∂t2

− grad div E −

grad ∂z

Здесь

∂

∂

∂

∂Ex

Ey

div E

=

∂x

+

∂y

,

grad = ex

∂x

+ey

∂y

.

(1.6.2)

19

Как и в предыдущем разделе, задача состоит в переходе к уравнениям для огибающих E . Вывод уравнения близок к приведенному в разделе (1.5).

Оценки значимости различных членов основываются на том, что в простейшем варианте квазиоптического уравнения для случая монохроматического излучения

2ik

∂E

+ ∆

E

+ 4π

k2

(1.6.3)

0

0 δP = 0

∂z

ε0

все члены для оценок считаются одного порядка величины ~ E

/ r2 ,

так

что

характерный

масштаб

продольного

изменения огибающих

r ~ k r2

0

(

~ r−1,

∂/ ∂z ~ (k r2 )−1)

и δP

~ E /(k

0

r )2

. Для расширения области

0

применимости уравнений мы включим в них также поправочные члены

~ (k r )−1		(E	/ r2 ) , пренебрегая членами более высокого порядка малости
0
~ (k r )−2		(E / r2 ) .
0				на	совпадающих	с	предыдущими
	Не		останавливаясь

преобразованиях выражений вида ∆ E , ∂2E2 и т.д., отметим очевидное

∂z

соотношение

	(1.6.4)
− grad div E = − grad div E exp(ik0 z −iω0t) .

Новым специфичным для анизотропной среды обстоятельством служит присутствие в третьем и последнем членах левой части (1) продольной компоненты электрического поля. Ее можно выразить через поперечные компоненты поля и их пространственные производные. Для этого запишем (1.2.32) в форме

div

D(l ) +ik

D(l ) + ∂Dz(l )

+ 4πdiv

δP

= 0.

(1.6.5)

0

z

∂z

(1-ый

Члены этого уравнения имеют, соответственно,

величину ~ E / r

член),

~ k

D(l)

(2-ой

член), ~ D(l) /(k r2 ) (3-ий

член) и ~ D(l)

/(k2r3 )

0

z

z

0

z

0

(последний член). Отсюда следует, что последний (нелинейный) член пренебрежимо мал по сравнению с первым членом. Сохраняя в этом соотношении только линейные члены, перепишем его в виде

	2		i	3	3
E3 = −	1	∑ε3m Em +		∑	∂	∑εml El ,	(1.6.6)
	ε33 m=1		k0ε33 m=1		∂xm l=1
где E1 = Ex , E2 = Ey , E3 = Ez , x1 = x, x2 = y, x3 = z . Для							рассматриваемых

широких пучков основным в правой части (6) является первый член. Тогда, учитывая второй член как добавку и пренебрегая в нем малым членом с производной в продольном направлении, найдем

		1	2	i	2	∂E
E3	= −		∑ε3m Em +		∑αml	m ,	(1.6.7)
		ε33 m=1		k0 m,l=1		∂xm

20

	где			εlmε33 −εl3ε3m
	α	ml	=		(m,l =1,2) .	(1.6.8)
				ε2
				33

Для среды с пренебрежимо слабой анизотропией первый член в левой части (7) отсутствует, а во втором члене αml =δml , так что в этом случае

приходим к (1.5.19).

Ввиду анизотропии среды изменения возникают и в описывающем частотную дисперсию 3-м члене (1). Дисперсия определяется заданием фурье-разложений поля и электрической индукции (знак вещественной части опускается):

E = exp(ik0 z)∫Eδω exp[−i(ω0 +δω)t]dδω,

D(l ) = exp(ik0 z)∫εˆ(δω)Eδω exp[−i(ω0 +δω)t]dδω.

Теперь

− c12 ∂2∂Dt2(l ) = exp(ik0 z)∫kˆ 2 (δω)Eδω exp[−i(ω0 +δω)t]dδω,

где введен тензор

kˆ 2 (δω) = (ω0 +2δω)2 εˆ(δω) . c

Разложение Тейлора этого тензора записывается в виде

(1.6.9)

(1.6.10)

(1.6.11)

∞

1

d

n ˆ 2

ˆ

2

(δω) = ∑

ˆ (n)

n

ˆ

(n)

k

k

Q

(δω)

,

Q

=

d(δω)

n

.

(1.6.12)

n=0

n!

δω=0

В частности, Q

представляет тензор обратной групповой скорости, а

Q

ˆ

(1)

– тензор квадратичной дисперсии. Теперь (10) примет вид

ˆ

(2)

1

2

(l )

N

i

n

n

∂

D

= ∑

ˆ (n) ∂

E

−

c

2

∂t

2

Q

∂t

n

exp(ik0 z −iω0t) ,

(1.6.13)

n=0

n!

где целое число N указывает порядок теории дисперсии. В правой части (13) присутствуют продольные компоненты векторов

V( j) = ∂jE/ ∂t j ( j = 0,1,2,...) . Их можно выразить через поперечные компоненты этих же векторов, продифференцировав (7) j раз по времени:

1

2

i

2

∂V

( j)

V3( j) = −

∑ε3mVm( j) +

∑αml

m .

ε33 m=1

k0 m,l=1

∂xm

V

Тогда для поперечных компонент вектора Q

ˆ

(n)

( j)

ˆ (n)

(

j)

2 (n)

ε3q

(n)

( j)

i

(n)

2

(Q

V

)p = ∑ Qpq

−

Qp3 Vq

+

Qp3 ∑αmn

ε33

k0

q=1

m,n=1

Применяя эти соотношения к (13), получим

	(1.6.14)
найдем (p = 1, 2)
∂V ( j)	(1.6.15)
m .
∂xn

21

−

1

∂2 Dp(l )

= exp(ik

z −iω t) ×

c2

∂t2

0

0

N

in 2

(n)

ε3q

(n) ∂n Eq

i

(n)

×∑

∑ Qpq

−

Qp3

+

Qp3

ε33

∂t

n

k0

n=0

n! q=1

Последний член левой части (1)

− grad

∂E

∂E

z

= − ik0grad Ez + grad

z

∂z

∂z

2	∂	n+1	Emn .
∑αmj
m, j=1	∂xj∂t
имеет вид
exp(ik		z −iω t) .
	0		0

После подстановки сюда (7) и введения двумерного вектора найдем

k

0

2

∂E

ik

grad

E

z

= i

grad

(ε

3

,E

) + grad

∑

α

mj

m

,

0

ε33

m, j=1

∂xj

− grad

∂Ez

=

1

grad

∂

(ε

3

,E

) .

ε33

∂z

∂z

(1.6.16)

(1.6.17)

ε3 = (ε31,ε32 )

(1.6.18)

(1.6.19)

В последнем выражении мы пренебрегли членом ~ (k0r )−2 (E / r2 ) .

Суммируя полученные выражения, мы получаем окончательно квазиоптическое уравнение с поправочными членами:

2ik

∂E + ∆

E

− grad

div

E

+i

k0

grad

(ε

,E

) +

ε33

0 ∂z

3

2

N

in

2

ε3q

∂n Eq

i

2

∂n+1E

+∑ep ∑

∑ Qpq(n) −

Qp(n3)

+

Qp(n3) ∑αmj

mn

+

ε33

∂t

n

k0

∂xj∂t

p=1

n=0

n! q=1

m, j=1

2

∂E

1

∂

4π

∂δP

+grad ∑αmj

m +

grad

(ε3 ,E )

+

2

ω02δP + 2iω02

=

0.

∂z

c

m, j=1

∂xj

ε33

∂t

Коэффициенты

pq(n)

Qpq(n)

(1.6.20)

совпадают

с

при

n ≠ 0, 2

,

при

этом

Q

Qpq(0) =Qpq(0) −k02δpq , а различие между Qpq(2) и Qpq(2) связано с обсуждавшимся

в предыдущем разделе вкладом члена ∂2E2 , см. (1.5.24).

∂z

Уравнение (20) описывает, в частности, перемешивание поперечных компонент огибающей вследствие анизотропии среды. Для изотропной среды (20) сводится к (1.5.18).

1.7. Квазиоптическое уравнение для метаматериалов

Для естественных сред в оптической области магнитная проницаемость μ близка к единице, и это условие до сих пор мы считали выполненным. В последнее время развиваются технологии создания искусственных сред с произвольными значениями эффективной

22

магнитной проницаемости, в том числе отрицательными. В этом разделе мы выведем квазиоптическое уравнение, описывающее распространение монохроматического излучения в изотропном метаматериале с нелинейными диэлектрической проницаемостью ε и магнитной восприимчивостью μ:

2			2
ε =ε0 +δε(| E | ),		µ = µ0 +δµ(| H | ),
2	|,	2	|,	(1.7.1)
|δε(| E | ) | |ε0		|δµ(| H | ) | | µ0

Imε0 = Im µ0 = 0.

Будем исходить из уравнений Максвелла для монохроматического излучения с частотой ω (комплексная форма записи):

					(1.7.2)
iωµH = c rot E,		iωεE = −c rot H .
Отсюда	можно			учетом зависимости		2
		выразить H	через E (с		δµ(| H | ) ,

строго говоря, определение этой зависимости сводится к решению трансцендентного уравнения):

	c
H = −i	ωµ	rot E.	(1.7.3)

С учетом этого соотношения получаем замкнутое уравнение для напряженности электрического поля

1

ω2

rot

µ

rot E

=

c

2

εE,

(1.7.4)

или

∂2

ω2

1

∂z

2

E + ∆ E +

c

2

εµE

−grad div E − µ[grad

×rot E] = 0 .

(1.7.5)

µ

В невозмущенной прозрачной линейной среде (δε =δµ = 0 ) решение имеет вид плоской волны с зависимостью напряженностей поля от z (в

комплексной форме записи) вида exp(ikz), где волновое число k = ωc 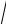ε0µ0 ,

причем считается ε0µ0 > 0 (в противном случае распространение волны

невозможно). Существенно, что напряженности электрического и магнитного поля связаны соотношениями

	ε0					ε0
H =	µ0	[ez ×E],		H	=	µ0		E		.	(1.7.6)
Для вывода квазиоптического уравнения полагаем
											(1.7.7)
E = Re{Eexp(ikz)},					H = Re{Hexp(ikz)}.

В стандартных для квазиоптики приближениях получаем искомое уравнение в виде

23