Решение. Перепишем (15) в форме, в которой все малые члены собраны в правой части уравнения (хотя их порядки величины различны):

	2			2	2			2		ωp2
P	+Ω	P	= −γ P +(Ω		−ω	)P −κ	P		+		E cos(ωt).
					0	2				4π

По смыслу задачи, внешняя сила с частотой ω возбуждает колебания на второй гармонике, частота которой Ω = 2ω близка к собственной частоте осциллятора ω0 . Последнее обстоятельство обеспечивает гистерезис и

определяет принятые ниже соотношения порядков величин. В нулевом порядке теории возмущений, как и ранее,

	2	P		= 0,				P			= p cos(Ωt +ϕ) .
P	+Ω
0			0						0		0
В первом порядке
	2				ωp2																							ωp2
P	+Ω	P		=			E cos(ωt),											P			= p	cos(ωt),					p =					E .
					4π																							12πω2
1			1																1		1						1
Во втором порядке												1
	2	P		= −κ				P		2	= −			κ					2	[1+cos(2Ωt + 2ϕ)],
P	+Ω											2					p
2			2				2		0							2			0
P	= p		+ p			cos(2Ωt + 2ϕ),															p	= −	κ		p2		p	=	κ		p2
																									2 0 ,					2		0 .
2	20				22																20		8ω2				22		24ω2
Наконец, в третьем порядке
	2	P		= −2κ					P		P −		κ		P		2					+(Ω		2	−ω	2	)P .
P	+Ω																		−γ P
3			3					2		0	2			2		1					0				0		0

Периодическое решение последнего уравнения возможно при условиях типа (42), откуда вытекает уравнение вида (45) (вывести самостоятельно).

2.1.3.Другие осцилляторные модели

Модель осцилляторов эффективна для решения большого числа

линейных и нелинейных оптических задач. Упомянем здесь только некоторые из них.

Модель связанных осцилляторов

При описании комбинационного рассеяния (следующая часть Пособия) излучения на молекулах рассматривается возбуждение оптическим излучением молекул, которые помимо частоты ω0

электронного перехода характеризуются более низкой частотой

молекулярных колебаний Ω	0	, Ω	0	/ω ~ 10−2	. Поэтому медленные
				0

колебания ядер около положения равновесия модулируют оптическую поляризуемость молекул. Феноменологическая модель связанных колебаний отклонений от равновесных положений координат электронов x и молекул Q имеет вид [6]

39

2

e

+ 2

η

,

x

+γ x

+ω0 x

=

m

E

m

Qx

η

(2.1.52)

2

2

.

Q

+ ΓQ +Ω0Q =

x

M

Здесь m и M – массы электрона и молекулы, соответственно, а величина η пропорциональна параметру Плачека (производной поляризуемости молекулы по Q). Согласно (52) ядра раскачиваются силой, пропорциональной квадрату колебаний электронов, и резонансное возбуждение молекулярных колебаний достигается, когда разностная частота колебаний электронов (разность частот оптических колебаний) приближается к собственной частоте Ω0 .

Экситонные резонансы и пространственная дисперсия

В предыдущих разделах мы игнорировали эффекты пространственной дисперсии ввиду их слабости в обычных условиях из-за малости отношения межатомных расстояний к длине волны оптического излучения. Однако во многих диэлектриках и полупроводниках могут возбуждаться экситоны – квазичастицы, отвечающие электронному возбуждению и мигрирующие по твердому телу без переноса электрического заряда и массы [7]. Один из типов экситонов – экситоны ВаньеМотта – можно интерпретировать как водородоподобное связанное состояние электрона проводимости и дырки. Размеры таких экситонов могут значительно превышать межатомные расстояния в полупроводнике, в связи с чем роль эффектов пространственной дисперсии возрастает, особенно при близости частоты излучения к резонансной частоте экситона.

Одна из простейших теорий резонансного возбуждения экситонов оптическим излучением, справедливая для изолированного экситонного электродипольного резонанса в кубическом кристалле, отвечает следующей осцилляторной модели [8]:

		2			ω		ωpe2
					0
P	+γ P +ω		P	−		∆P =		E .	(2.1.53)
		0			Me		4π

Здесь поляризация излучения фиксирована и обозначения близки к использованным в п. 2.1 для модели Друде – Лоренца, ср. с (2). Так, P – экситонная составляющая поляризованности, ω0 – собственная частота

экситонного перехода, γ – постоянная затухания, E – электрическая напряженность поля излучения. Специфически экситонными параметрами

	служат Me				– эффективная масса экситона (изотропная модель) и
	ω2	=	2d 2		– квадрат плазменной экситонной частоты (d – матричный
			ω0V0
	pe

элемент дипольного экситонного перехода, V0 – объем элементарной

40

ячейки кристалла). Пространственная дисперсия учтена в (53) членом с оператором Лапласа .

Как и (2), уравнение (53) линейно и описывает линейную восприимчивость среды. Чтобы найти ее, положим

	1	E exp(ikz −iωt) + к.с.,		1	Pexp(ikz−iωt) + к.с.,	(2.1.54)
E =	2		P =	2

где ω и k – частота и волновое число излучения. Подстановкой (54) в (53) получаем

P = χ(1) (ω,k)E ,

(2.1.55)

где (ср. с (9))

χ

(1)

(ω,k) =

ωpe2

1

.

(2.1.56)

π

ω

2

−iγω −ω

2

+

ω

2

4

0 k

0

Me

Согласно

(56),

линейная

восприимчивость χ(1) (ω,k)

зависит не

только от

частоты

излучения, но и от квадрата волнового числа

(пространственная

дисперсия).

Модель

отвечает

изотропной

негиротропной

среде. С учетом

следующего

из волнового

уравнения

соотношения k2

=

ω2

[1+ 4πχ(1) ]

дисперсионное соотношение сводится к

c2

квадратному уравнению для определения зависимости линейной восприимчивости от частоты. Особенности линейных дисперсионных соотношений вблизи экситонных резонансов рассмотрены в [2].

Обобщением (52) на нелинейный случай служит уравнение (ср. с

(13))

2

ω

2

3

ωpe2

0

P

+γ P +ω

P

−

∆P +κ

P

+κ

P

+... =

E .

(2.1.57)

0

Me

2

3

4π

Это уравнение описывает, в частности, изложенные выше эффекты генерации гармоник, суммарных и разностных частот, а также гистерезисные явления.

Задание 2.6. Исходя из (54) и (57) при κ3 = 0 , найти квадратичную

восприимчивость, отвечающую генерации второй гармоники.

Указание. Как и для нелинейной модели Друде – Лоренца, использовать нерезонансный вариант теории возмущений.

Оптическая нелинейность наноструктур и метаматериалов

Недавний впечатляющий прогресс в технологии создания искусственных композитных оптических сред – наноструктур и метаматериалов – делает реальной разработку сред с заранее задаваемыми и управляемыми характеристиками, в том числе с отрицательными

41

диэлектрической и магнитной проницаемостями (см. также п. 1.7). В твердотельных наноструктурах (гетероструктурах) формируются пространственные неоднородности с масштабами от единиц до сотен нанометров, внутри которых возможна локализация внешнего оптического излучения и различных элементарных возбуждений твердого тела. Например, согласно теории Ми [9], для шарика малых размеров с диэлектрической проницаемостью εs , находящегося в материале с

диэлектрической проницаемостью εm , соотношение между действующим полем Es и полем в объемном материале Em следующее

Es	~	εm −εs				.	(2.1.58)
E
		ε	m	+ 2ε	s
m

Резонансное усиление поля, когда знаменатель дроби в правой части (58) приближается к нулю, происходит вблизи частоты излучения ω =ωp / 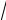3 , где ωp – плазменная частота (см. (2.1.3)), и интерпретируется как

возбуждение коллективных колебаний электронов в среде (мода Фрелиха). Более общее условие резонансного усиления в соответствии с теорией Ми формулируется в виде εm /εs = −( j +1) / j , j =1,2,3,... Естественно, что при

таком усилении поля возрастает роль нелинейности среды. Некоторые нелинейно-оптические свойства металлических частиц рассмотрены в [10].

Более изощренные метаматериалы могут включать металлические проволочки и кольцевые резонаторы с размерами, меньшими длины волны излучения. На рис. 2.4 представлена схема такой двумерной композитной структуры с квадратной решеткой периодических ячеек из проводящих проволочек (обеспечивающих, главным образом, отрицательную вещественную часть эффективного показателя преломления) и разомкнутых кольцевых резонаторов (приводящих к отрицательной магнитной проницаемости).

Рис. 2.4. Схема композитного метаматериала, состоящего из проводящих проволок (вертикальные линии) и разомкнутых кольцевых резонаторов. Нижняя вставка указывает геометрические параметры резонаторов и

42

поляризационную структуру излучения. На верхней вставке представлена расчетная модель эквивалентного осциллятора [11].

Нелинейность композитной структуры определяется двумя факторами. Во-первых, имеется вклад от зависимости от интенсивности объемной диэлектрической проницаемости диэлектрика-заполнителя

εD =εD (| E |2 ) . Во-вторых, решетка резонаторов также приводит к

нелинейному вкладу, так как емкость резонаторов и, соответственно, их собственная частота зависят от локального электрического поля в узком зазоре. В свою очередь, интенсивность поля в зазоре зависит от электродвижущей силы в цепи резонатора, которая индуцируется магнитным полем. Поэтому эффективная магнитная проницаемость µeff

должна зависеть от средней напряженности магнитного поля Н. Выполненный в [11] анализ показал, что при определенных

условиях эффективные нелинейные диэлектрическая и магнитная проницаемости могут быть записаны в виде

	2		ωp2					(H) =1+	Fω2
εeff	=εD (| E |	) −				,	µeff				. (2.1.59)
			ω(ω −iγ	ε	)				ω2 (H) −ω2	+iΓω
									0NL
Здесь ωp ≈ (c / d )[2π / ln(d / r)]1/ 2								– эффективная плазменная частота,
γε	= c2 / 2σS ln(d / r) , d –						период решетки (см. рис. 2.4), r – радиус
проволочек,		F =πa2 / d 2 1 , Γ = c2 / 2πσa min(h,δ) ,								σ – проводимость

металла проволочек, S – эффективная площадь их сечения ( S ≈πr2 при

δ > r и S ≈πδ(2r −δ) при δ < r , где δ = c /							2πσω – толщина скин-слоя, h
– толщина слоя в кольцевом резонаторе (см. рис. 2.4). Наконец,
ω2	(H) =	c 2			dg		(2.1.60)
					2
0NL
		a			πhεD (| Eg (H) | )

– собственная частота осцилляций в присутствии внешнего поля конечной амплитуды и Eg – напряженность электрического поля в области зазоров

резонаторов. Согласно (59) и (60), резонансная частота искусственной магнитной структуры зависит от амплитуды внешнего магнитного поля, и это приводит к зависимости от интенсивности магнитной проницаемости µeff . В характерных условиях высокодобротных резонаторов собственная

частота осцилляций ω0NL является многозначной функцией напряженности

магнитного поля, что вызывает различные гистерезисные явления. Заметим, что реальные размеры микрорезонаторов заметно больше

размеров ячеек обычных кристаллов и даже размеров экситонов в полупроводниках. Поэтому можно ожидать, что для такого метаматериала могут быть сильно выражены анизотропия и пространственная дисперсия

– факторы, которые не учитывались в приближенной модели.

43