Дискретная математика. Расчёт функции Эйлера для составных чисел.

65. Преобразовать последовательность a,b,c,dв уникальный набор неповторяющихся цифр: например,,, 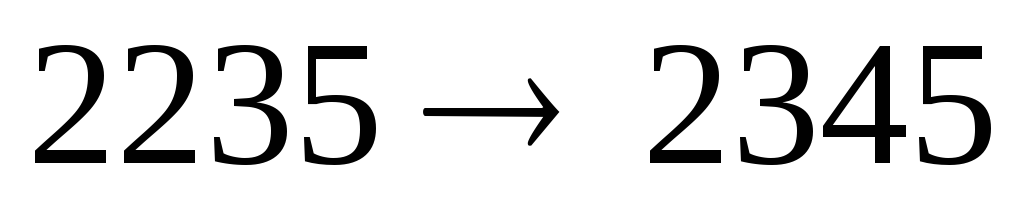наборы, не имеющие повторений, сохраняются, и рассчитать следующие функции Эйлера,,,,,

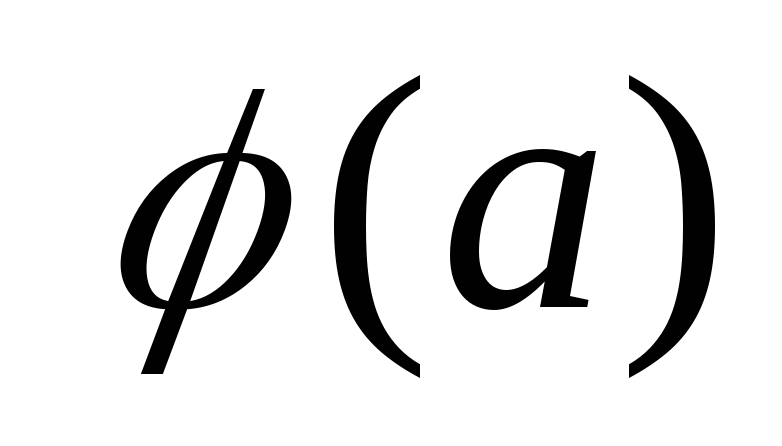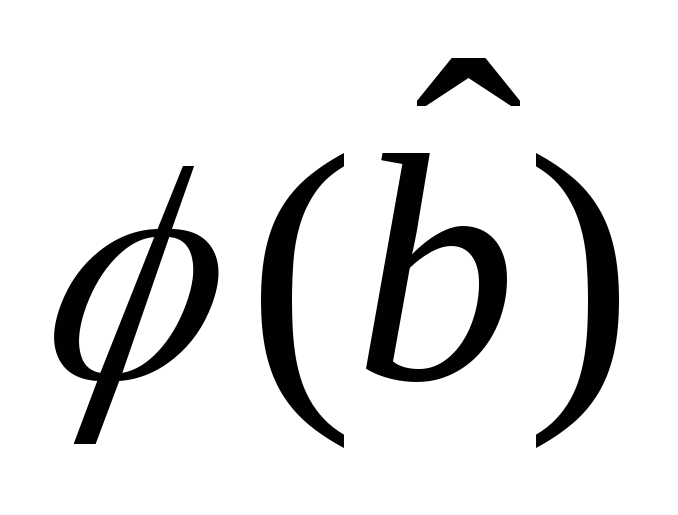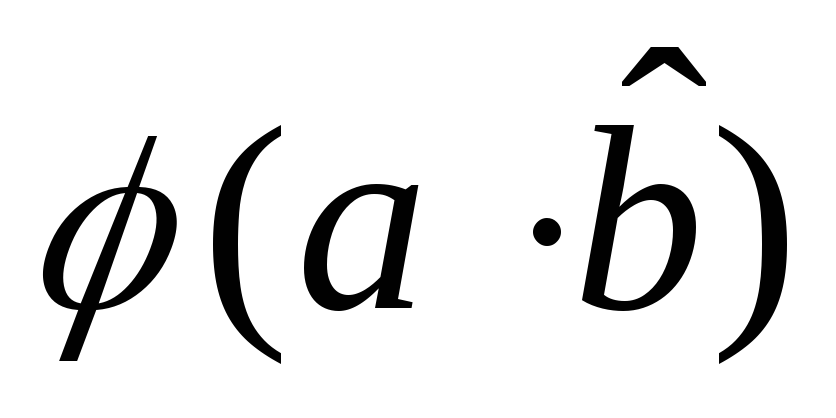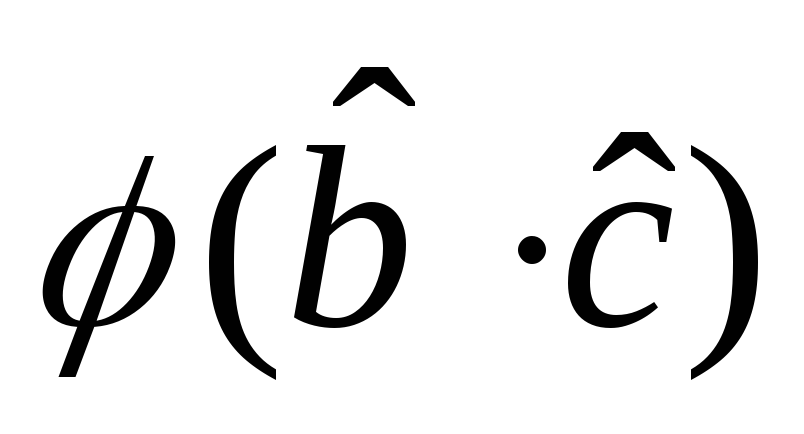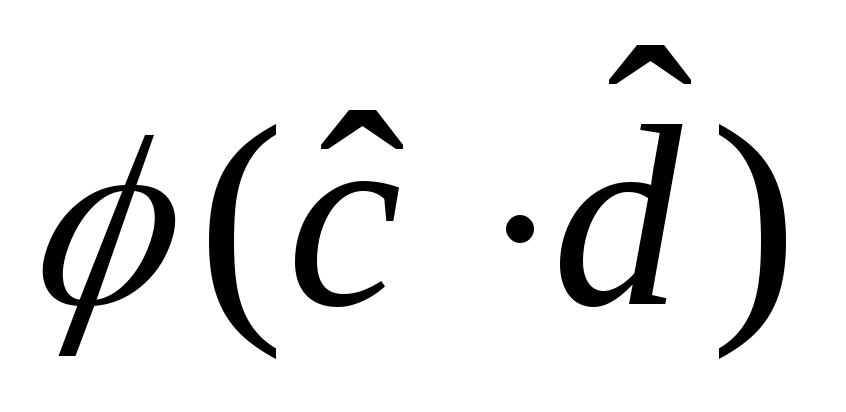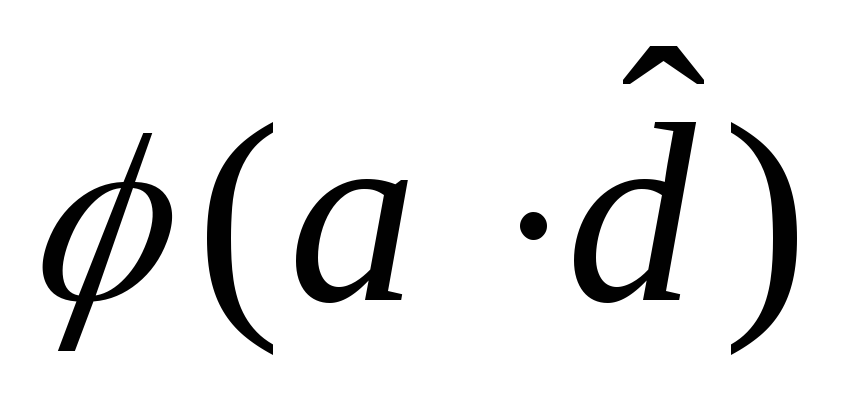
14. Какие из модулей удовлетворяют СТАНДАРТНЫМ Требованиям для применения алгоритмов Диффи-Хелмана, Масси-Омуры, RSA.

Хроматические полиномы. Задача о раскрасках.

66. (в пяти вершинном исполнении –очень Дорогая задача).

1. (1+ задача) Построить хроматический полином по пустым графам и кликам для 4-хвершинного графа, пример

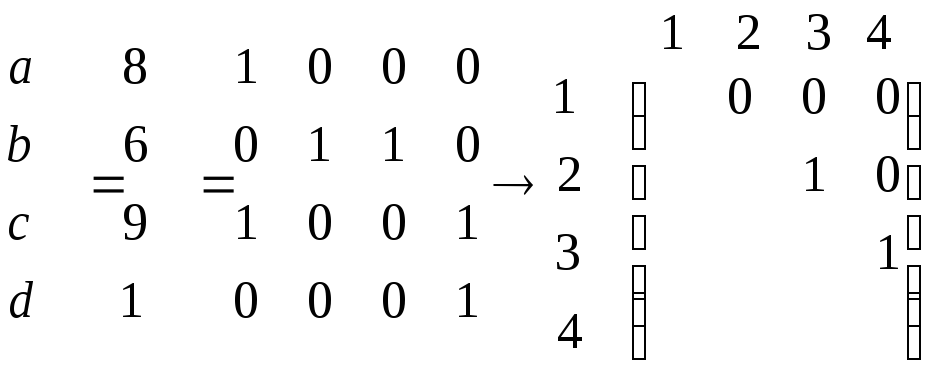
2. Вариант 2 Построить хроматический полином по пустым графам и кликам для стандартизованного 5ти рёберного и 5-ти вершинного графа.

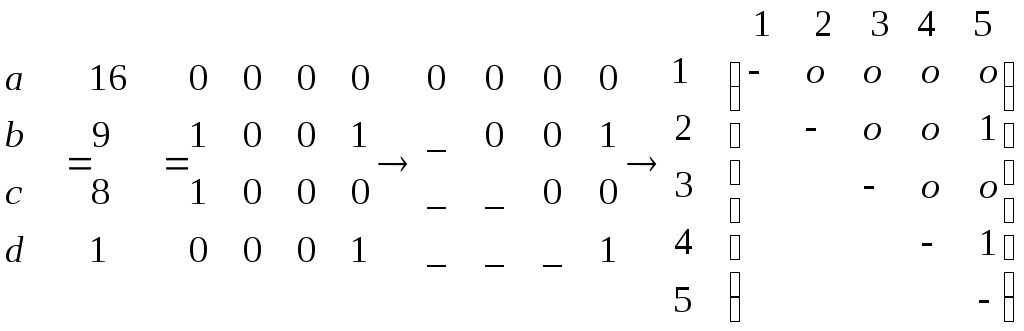Переводим данный граф СТАНДАРТНЫМ ОБРАЗОМ в пяти-рёберный: для этого рассматриваем позиции нечётные в следующей нумерации. (В полном пяти вершинном графе – клике 10 рёбер, но нам нужна ровно половина – это связано с экспоненциальной зависимостью от числа наличествующих и пустых рёбер двух ветвей алгоритма.).

точнее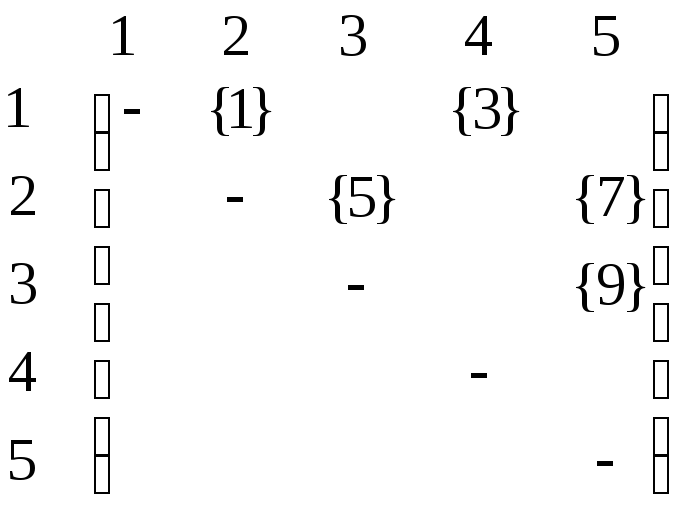

слева-направо (номера ) и сверху вниз – РАСТРОВАЯ развёртка).

Конкретнее, рассматриваем ровно 5 позиций: позиции 1 и 3 в первой строке, 1 и 3 во второй (каждый раз счёт идёт от диагонали) позицию 2 в третьей и ЗАМЕНЯЕМ в порядке ОЧЕРЁДНОСТИ избыточные ЭЛЕМЕНТЫ на НЕДОСТАЮЩИЕ. (Мы рассмотрели нечётные позиции при обходе над-диагонального треугольника

пока в графе есть 2 ребра.

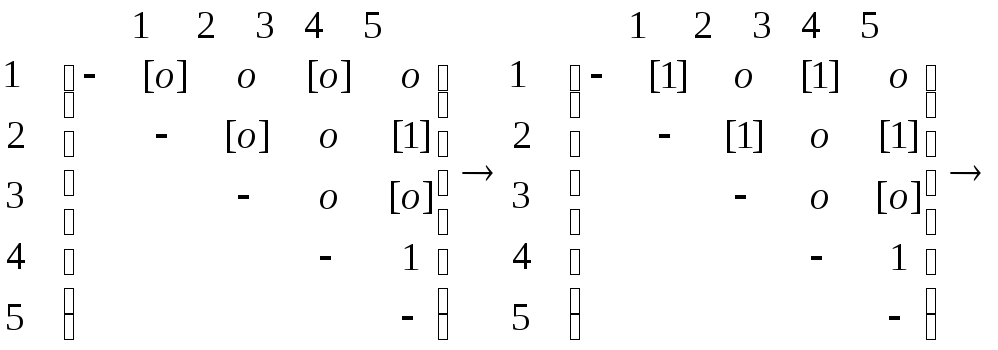
МЫ ЗАМЕНИЛИ первые три НУЛЯ (нечётной под-Последовательности ) на ТРИ ЕДИНИЦЫ.

3. Вариант 3 (эта часть решается по указанию преподавателя вместо части b) … для 5-ти вершинного графа, полученного из заполнения верхнетреугольной матрицы инцидентности симметричного графа двоичными записями чиселabcd(числа пишутся в каждое в свою строку так, чтобы последний разряд был в последнем столбце).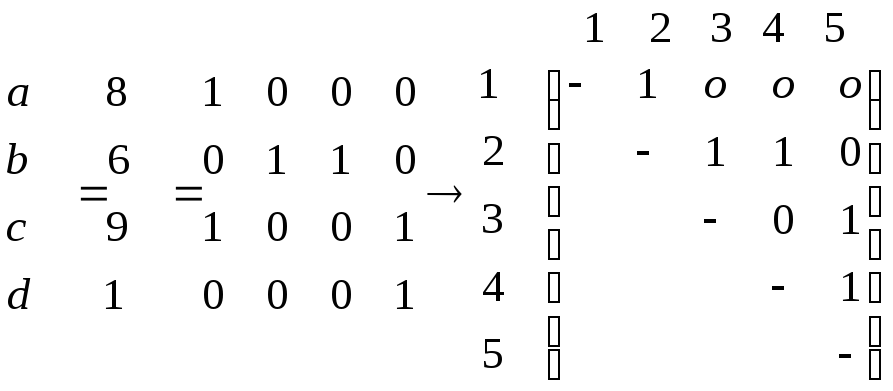(Недостаток – этой части неконтролируемый уровень сложности, что преодолено в частиb, если числапроведённыхинепроведённыхрёбер оба равны 5.(всего может быть 10 рёбер в полном графе)).

Логика. Нормальные формы. Теорема Поста.

Построить ДНФ, ПНФ, КНФ для функций двух переменных, чьи столбцы значений определены монотонной комбинацией на основе личного номера

Теория.

Классы Поста.

По теореме Поста Функциональная система полни т.и т.т.к. все её функции не содержатся ни в каком из 5-ти классов Поста.

Классы Поста это

• Линейные функции

• Монотонные

• Самодвойственные

• А также функции сохраняющие 0

• И сохраняющие 1

Функции сохраняющие 0:

Функции сохраняющие 1 – функции имеющие значение 1 на наборе из всех единиц: (половина всех функций принадлежит этому классу)

Монотонные функции – это функции, которые не убывают: если для всех ситуаций ,

,

либо ,либо,

Но нет ни одной ситуации, когда при условии

имеет место

,

Самодвойственные функции – по сути это нечётные функции, если заменить 0 на -1. Очевидно, комбинация (точнее, композиция) нечётных функций нечётна

Самодвойственные функции это те, которые на всех противоположных наборах имеют противоположные же логические значения , илиили.

Линейные функции - это функции вида

.

Очевидно класс линейных функций замкнут относительно композиции.

Пример решения

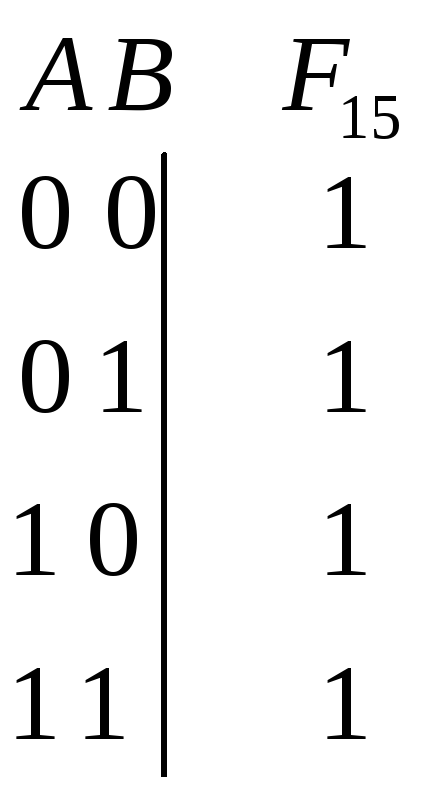
Возьмём набор функций 3,2, 14, 15, (преобразуем личный номер, точнее его монотонную комбинацию, в двоичное представление, транспонируем столбцы – получаем столбец значений логической функции):

3=0011

2=0010

14=1110

15=1111 (ПО Нашему соглашению при транспонировании младший разряд оказывается снизу!!).

,,,

Разберём - остальное делается аналогично

Строим КНФ

Общая формула

.

(произведение дизъюнктов вида по наборам где функция принимает значение 0)

Далее строим ДНФ

Строим функции вида , которые имеют значение 1 на единственном наборе, том на котором функция равна 1,

Наша функция – это Очевидно – задаётся суммой всех произведений, соответствующих её единичным наборам.

итого

Общий подход

(сумма всех конъюнкций по наборам, где функция принимает значение 1 ).

По ДНФ построим полиномиальную форму

преобразуем в

(пояснение мы можем заменить + на , потому и только потому, что не более 1 слагаемого

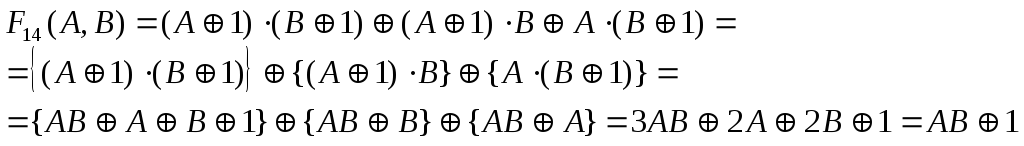
таким образом:

функция нелинейна, т.к. в её ПНФ присутствует - смешанный член.

(Не сохраняет 0),

(Не сохраняет 1),

(Не монотонна (например, последний набор 0, первый 1:)), в общем случае на по Парето сравнимых наборах, на большем наборе должно быть не меньшее значение.

не самодвойственна, например, потому что

Данная функция Шефферова, образует базис.

По той же схеме - безо всяких упрощений - решаем

,

, она очевидно, линейна, монотонна, самодвойственна, сохраняет 0, сохраняет 1,

- монотонна, линейна, неСамодвойственна, потому, что есть контр пример- противоположные наборы с одинаковыми значениями (для тех же целей подойдёт пример).

Аналогично,

- монотонна, линейна, неСамодвойственна, потому, что есть контр пример- противоположные наборы с одинаковыми значениями (для тех же целей подойдёт пример).

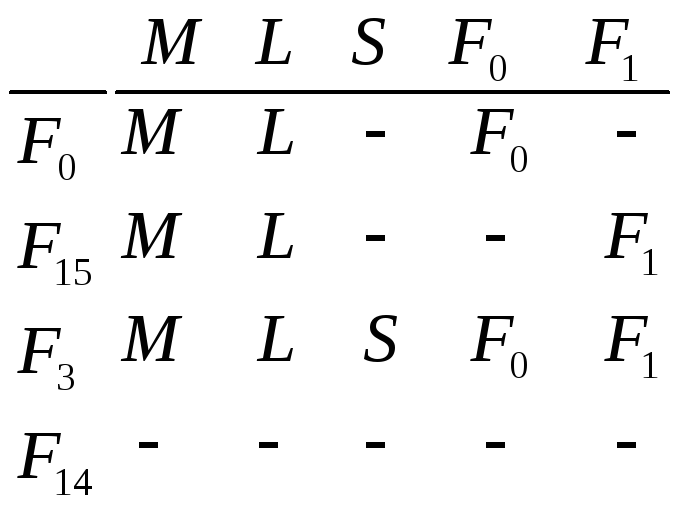
Ответ: единственный минимальный базис составляет функция

Для полноты примеров рассмотрим часто используемые системы функций():

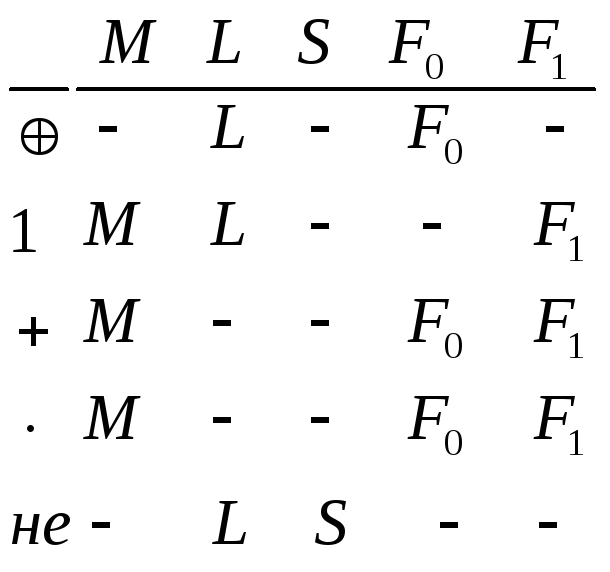
Найдём полные базисы в этой системе. Это можно делать и безсистемно, но в данной системе базисов много, как всегда начнём с поиска наиболее узких мест:

Нам нужна

Одна из функций + или , чтобы избежать попадания в классL

Одна из функций "не" и "исключающее или", чтобы избежатьи М.

Одна из пары функций и «не» , чтобы избежать.

Чтобы удовлетворить второму признаку нужно либо образовать пары с функцией "не"

,

Либо с функцией

но это будут тройки ,.

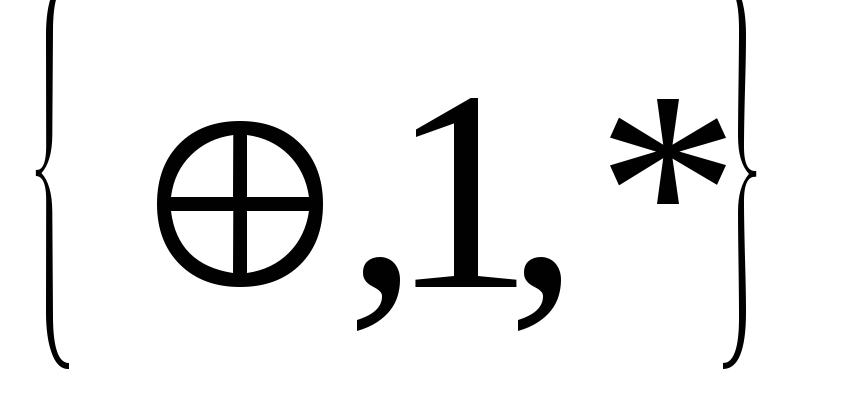Других (минимальных) базисов здесь нет.

Ответ: в представленной системе минимальные базисы образованы наборами функций: ,,,,

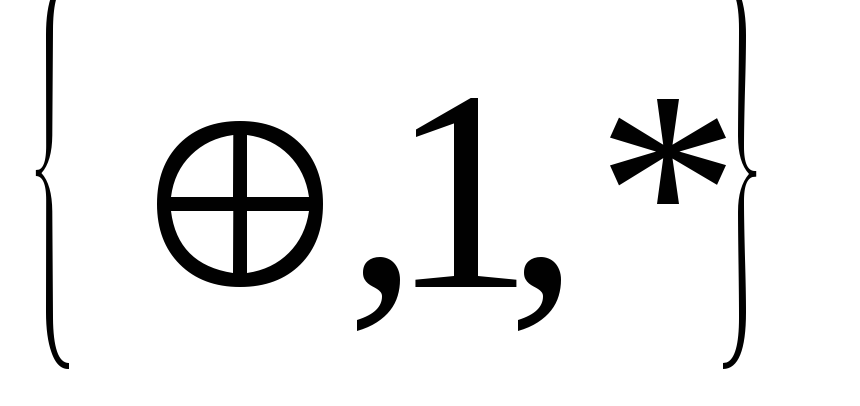Теоретическое замечание:

объединение базисов ,порождает КНФ и ДНФ (имея отрицание и логическое "и" или логическое "или" можно получить оставшийся компонент).

Набор - базис полиномиальных нормальных форм.

67. Для функци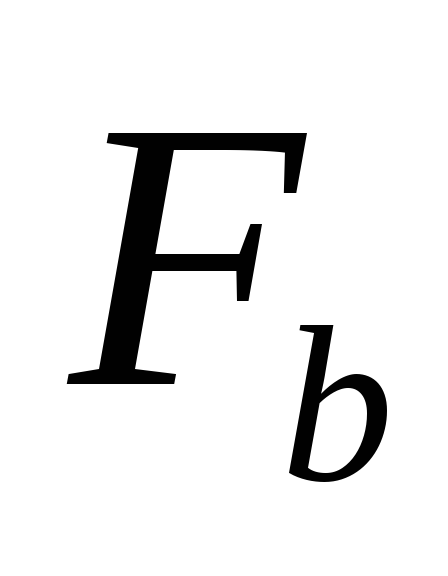й ,,и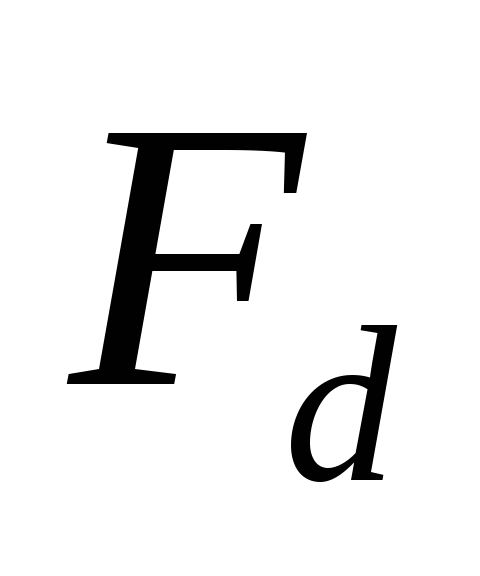полученных из чиселabcdв двоичном представлении (каждое число – столбец логических значений функции). (При совпадении увеличить одно из чисел на 1, пока не исчезнет совпадение – таким образом, в любом случае будет 4 функции).

4. Выяснить отношения следствия

5. Написать СКНФ, СДНФ, СПНФ (СПНФ пишется только для первых двух функций: и).

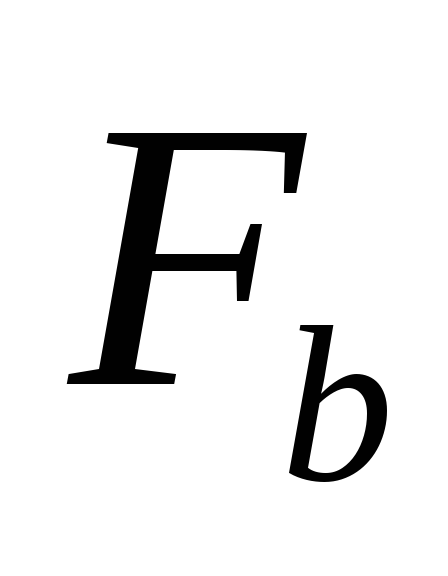6. Идентифицировать данные функции, а также их отрицания (максимум 8 функций).

7. Определить какие переменные существенны для 8ми функций из предыдущего пункта

Пустьдвоичная запись числа,

тогда 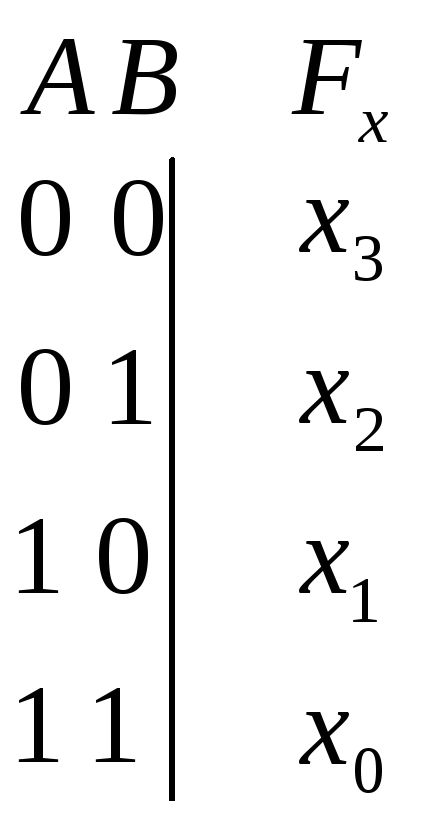Пример

1. (в дополнение к предыдущей задаче)Классифицировать функции по всем классам Поста. Найти минимальные базисы, т.е. найти все такие наборы которые перестают быть базисными при вычеркивании каждой входящей в них функции. Например к Шефферовой функции не надо добавлять никакую (она сама базис).

1. Для функци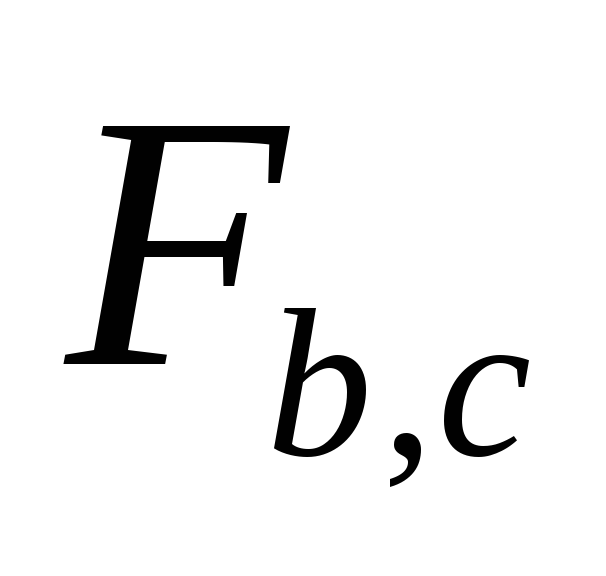й ,,и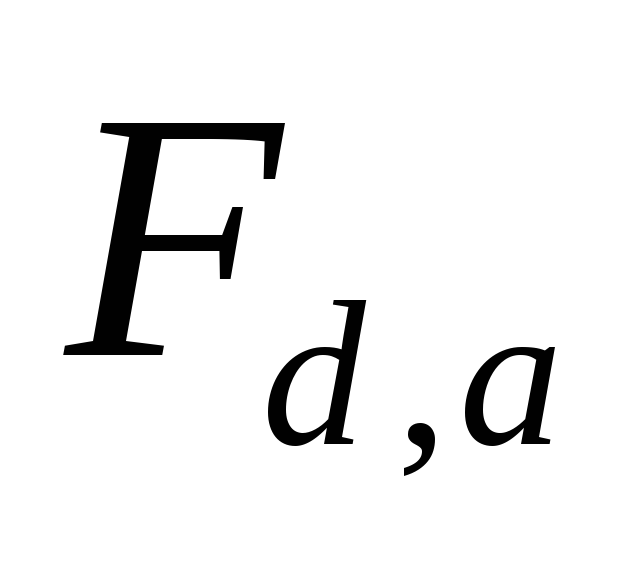(ИКТ использует 4 функции, остальные факультеты - для краткости три) где функция:

, гдедвоичная запись числа, (например) сделать то же самое:

1. Написать СКНФ, СДНФ, СПНФ (для двух функций: и).

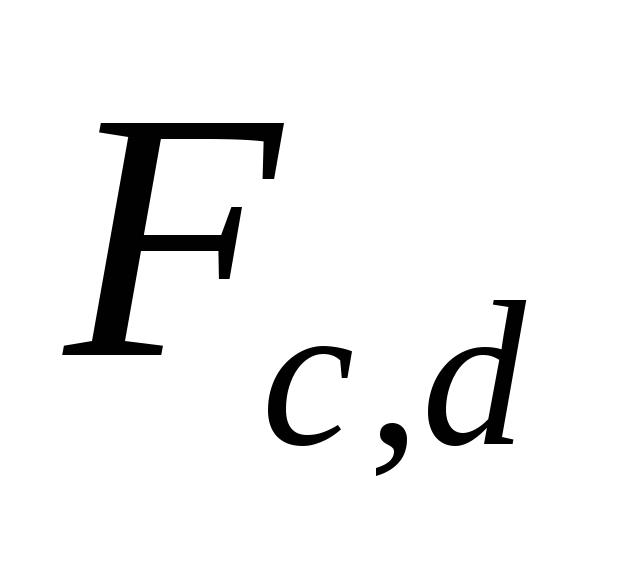2. Рассмотрев данные функции плюс 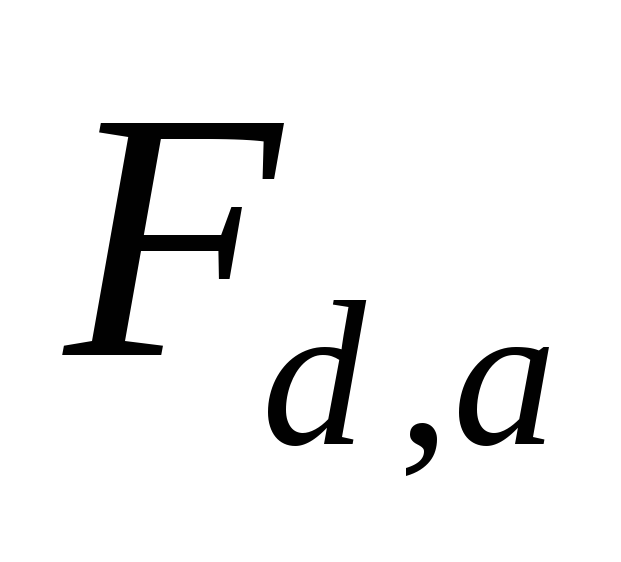, а также их отрицания (максимум 8 функций), выяснить отношения следствия и эквивалентности

3. определить какие переменные существенны для данных функций (для существенных переменных привести пары доказывающих наборов значений лог. переменных, для не существенных отметить (выписать) пары наборов, отличающихся только значением данной переменной, с указанием общего значения функции.

4. Классифицировать функции по всем классам Поста. Указать причины (не) монотонности, (не) самодвойственности, (не) линейности.

5. Руководствуясь теоремой Поста найти минимальные базисы, т.е. найти все такие наборы которые перестают быть базисными при вычеркивании каждой входящей в них функции. Например к Шефферовой функции не надо добавлять никакую (т.к. она сама базис).

6. *(по просьбе преподавателя).Выяснить отношения следствия

69. Алгебра высказываний закодируем