2. Множественная регрессия. Оценка параметров множественной регрессии

Множественная регрессия - уравнение связи с несколькими независимыми переменными:

. (1)

где у - зависимая переменная (результативный признак); x₁, x₂, , x_p - независимые переменные (факторы).

Для построения уравнения множественной регрессии чаще используются следующие функции:

- линейная:

, (2)

- степенная:

(3)

- гиперболическая:

(4)

- экспоненциальная регрессия:

(5)

- и другие.

Одним из наиболее распространённых методов, используемых для оценки параметров уравнения множественной регрессии является метод наименьших квадратов (МНК).

Система уравнений, используемая для оценки параметров линейной регрессии (2.2) имеет вид:

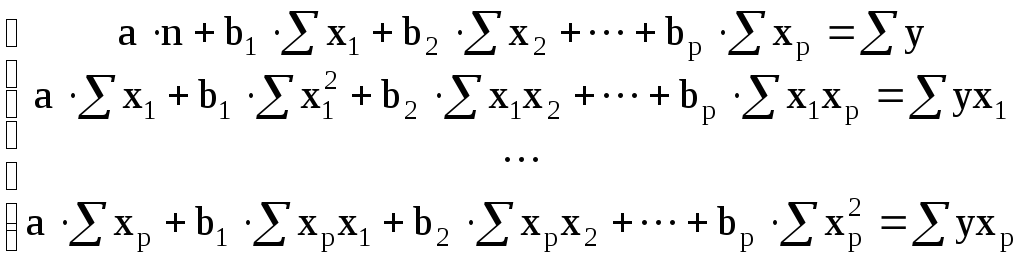(6)

Решая систему уравнений, получаем искомые параметры множественной регрессии. Для оценки параметров нелинейных регрессий используются методы линеаризации, аналогичные рассмотренным ранее.

Другим методом оценки является метод, связанный с использованием псевдообратной матрицы. Этот метод заключается в следующем:

- по исходным данным составляется система уравнений, описывающая зависимость выходной величины от входных, для каждой группы значений:

Обозначим:

A = {a, b₁, b₂,…, b_p}, вектор оценок параметров регрессии;

Y = {y_i}, - вектор значений зависимой переменной;

X = {x_ij}, , - матрица значений независимых переменных;

при этом p - количество независимых переменных, n - объем выборки.

Уравнение регрессии может быть представлено в следующим образом.

Для конкретного yi:

_i = a + b₁x_i1 + b₂x_i2 + ... + b_px_ip , (7)

или в матричном виде:

Y = A X,

где X =

1   x11   x12    ...     x1p 1   x21   x22    ...     x2p ... 1   xn1   xn2    ...     xnp

Обратите внимание на то, что в матрицу X дополнительно введен столбец, все элементы которого равны 1, т.е. условно полагается, что в уравнении (1.7) свободный член a умножается на фиктивную переменную xi0, принимающую значение 1 для всех i.

Можно показать, что для общего случая множественной линейной регрессии, коэффициенты уравнения могут быть определены из следующего соотношения:

A = (X^т∙X)^-1∙X^т∙Y. (8)

4. Основные способы представления динамических моделей

Важным этапом моделирования является создание математической модели исследуемой системы. На базе математической модели происходит анализ характеристик системы, при компьютерном моделирования на основе математической модели создается алгоритм программ для получения информации о поведении системы. Формальное описание объекта исследования необходимо также для взаимопонимания между специалистами разных областей, объединенных для решения какой-либо глобальной задачи.

1. Математические модели непрерывной системы

Как правило, модели динамических систем представляются в виде системы дифференциальных уравнений в форме Коши.

Система обыкновенных дифференциальных уравнений первого порядка, разрешенных относительно производных, может быть представлена следующим образом:

, (4.1)

где – непрерывное время;

– вектор интегрируемых переменных (их также называют кординатами состояния);

– вектор искомых переменных в алгебраических уравнениях (их также часто называют «алгебраическими» переменными) с согласованными начальными значениями ;

– вектор параметров.

Предполагается, что функция непрерывна по всем переменным в некоторой окрестности .

Линейные системы могут быть также представлены в векторно-матричном виде.