4. Метод авторегрессионной идентификации

Передаточную функцию линейной дискретной системы можно рассмотреть в виде:

, (1)

От такой формы прост переход к разностному уравнению системы: ,

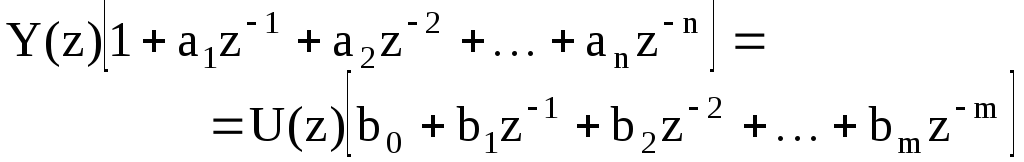, (2)

Здесь z^–1 может интерпретироваться как оператор запаздывания на такт, Окончательно запишем разностное уравнение:

, (3)

Выразим выходную величину системы:

, (4)

Таким образом, модель линейной дискретной системы полностью определяется коэффициентами a₀…a_n, b₀…b_m.

Задача идентификации сводится к нахождению оценок коэффициентов так, чтобы получить результат наилучшим образом согласующийся с экспериментальными данными, то есть, чтобы в каждый момент дискретного времени k получить достаточно малое рассогласование ε_k между выходным сигналом модели и системы :

, (5)

Предположим, что в ходе экспериментального исследования системы были получены последовательности дискретных отсчетов входного и выходного сигналов системы, Обозначим эти последовательности соответственно u₁…u_N, y₁…y_N,

Для каждого дискретного отсчета составим уравнение:

, (6)

получим систему из N линейных уравнений:

, , (7)

Решение системы относительно a и b дает искомые коэффициенты, Задачу идентификации можно коротко сформулировать так:

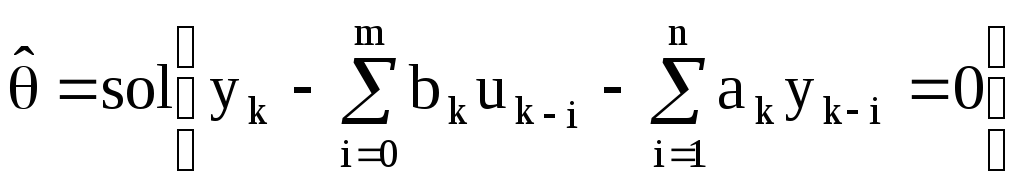, , (8)

Объединим все неизвестные коэффициенты в один вектор столбец θ, Сформируем также вектор-столбец, содержащий выходные координаты системы Y, Составим матрицу экспериментальных данных по следующему правилу. Каждая строка матрицы Ф соответствует моменту k дискретного времени и представляет собой вектор:

, ,

,

; , (9)

Используя введенные обозначения, запишем систему уравнений в матричной форме:

, (10)

При определенных условиях вектор θ может быть найден по формуле

(11)

где Ф^-1 - обратная матрица Ф,

Система (10) составлена, опираясь на предполагаемую структуру модели, которая лишь до некоторой степени близости отражает свойства реальной системы.

Требуется найти такой вектор θ, который давал бы модель возможно ближе, описывающую свойства системы,

При этом система уравнений (10) должна быть переопределенной (число уравнений гораздо больше числа неизвестных), но вместе с тем может быть несовместной, то есть не иметь точных решений, Обращение матрицы Ф становится невозможным, так она может не быть квадратной или может оказаться вырожденной (ее определитель равен нулю),

Поэтому необходимо искать псевдорешение [6], Псевдорешением системы называется такой вектор θ, который при подстановке в (10) дает вектор невязки , минимальный по евклидовой норме (метод наименьших квадратов),

Псевдорешение может быть получено одним из двух способов:

(12)

где Ф^T -транспонированная матрица Ф; Ф⁺ -псевдообратная матрица Ф,

5. Идентификация в векторно-матричной форме

Описание непрерывных стационарных систем управления в пространстве состояний имеет вид

(12.1)

где: X(t)— n-мерный вектор состояния;

U(t)— r-мерный вектор управления (входные управляющие воздействия);

Y(t)— m-мерный вектор выхода системы,

A– матрица состояния размера nxn;

B— матрица входа размера nxr;

C— матрица выхода размера mxn;

D— матрица обхода размера mxr.

Для строго реализуемых систем матрица D=0.

В задачу регрессионной оценки (идентификации) линейной стационарной системы (12.1) может входить определение ее структуры и параметров по наблюдаемым данным — входным и выходным сигналам функционирующей системы. Если структура системы задана, т. е. известны дифференциальные уравнения, описывающие систему, то в задачу входит определение ее параметров — коэффициентов дифференциальных уравнений — матриц действительных чисел A, B, C, D.

Для применения регрессионного анализа систему с непрерывным временем (12.1) следует представить в дискретной форме:

(12.2)

где:

T— шаг квантования (период дискретизации) по времени;

k— целые числа, , ;

C, D— матрицы дискретной системы тех же размеров, что и для исходной непрерывной системы.

Матрицы , имеют следующий вид:

, (12.3)

(12.4)

Если матрица A непрерывной системы не вырожденная, то матрицу можно представить в виде

, (12.5)

где E — единичная матрица n-го порядка.

Поскольку в уравнениях дискретной системы шаг квантования по времени T входит слева и справа, то его часто опускают и систему записывают в виде

. (12.6)

По известной матрице дискретной системы можно определить матрицу непрерывной системы, логарифмируя обе части уравнения (12.3). При этом следует иметь в виду, что в (12.3) следует применять матричный экспоненциал, а для обратного преобразования — матричный логарифм.

В случае неособенной матрицы A непрерывной системы уравнение (12.5) можно разрешить относительно матрицы B в виде

. (12.7)

Для достаточно малых значений шага квантования можно воспользоваться следующей приближенной формулой:

Таким образом, оценка матриц A и B непрерывной системы (12.1) осуществляется через оценку соответствующих матриц дискретной системы (12.2). При этом существуют более универсальные методы преобразования дискретной системы к непрерывной].

Систему разностных уравнений запишем в виде скалярных уравнений:

(12.8)

В задачу входит оценка (идентификация) параметров , , , .

Выпишем из (12.8) промежуточное уравнение:

(12.9)

В ходе эксперимента нужно запомнить g решений u(k), x(k), x(k+1) для идентификации параметров дискретной системы, причем . Решения системы (12.8) определяются в результате подачи на нее некоторых входных сигналов (управляющие воздействия). Чтобы проверить, насколько построенная модель точно имитирует или предсказывает данные наблюдений, необходимо сравнить их при одинаковых воздействиях. Эта процедура называется верификацией модели.

Составим матрицу из элементов x(k), u(k) размерностью (n+r)x1. Эта матрица будет представлять собой совокупность входных воздействий и выхода системы на момент дискретного времени k:

(12.10)

Составим матрицу из искомых коэффициентов уравнения (12.9):

(12.11)

С учетом (12.10), (12.11) запишем уравнение (12.9) в матричном виде:

. (12.12)

Сформируем вектор из элементов правой части уравнения (12.12) после g испытаний (значений, решений, наблюдений):

(12.13)

Выражая через , , получим , где

(12.14)

Размерность матрицы равна gx(n+r).

Считая, что вектор и матрица известны (входные и выходные сигналы), можно применить метод наименьших квадратов, в соответствии с которым получим следующее нормальное уравнение относительно искомых параметров уравнения (12.9):

(12.15)

Если матрица невырожденная, то оптимальная оценка параметров дискретной системы определяется в виде

(12.16)

Зная , для всех индексов i=1…n можно найти коэффициенты системы уравнений (12.8), т. е. матрицы , , а затем, например, по формулам (12.3), (12.7) найти матрицы A, B непрерывной системы (12.1).

В случае, когда матрица вырожденная или плохо обусловленная, при решении нормального уравнения (12.6) прибегают к псевдообращению, например, используют псевдообратную матрицу Мура–Пенроуза.

Расчет вектора состояния дискретной системы можно произвести по соотношению

, (12.17)

где X(0) — начальный вектор состояния системы в момент времени, равный нулю.

Для регрессионной оценки матриц уравнения выхода C и D используются те же способы и приемы, которые были описаны для оценки матриц A и B. В случае невырожденной матрицы одновременная оценка матриц C и D может быть получена с помощью матричного уравнения следующего вида:

, (12.18)

где

,

Примечание. При верификации модели на вход модели и на реальную систему подают сигналы, которые не использовались при идентификации параметров и сравнении выходных сигналов модели и реальной системы.