
- •Оглавление
- •3. Прямая линия в пространстве 22
- •4. Прямая и плоскость 25
- •1. Простейшие задачи на плоскости 26
- •I. Векторная алгебра
- •1. Определение вектора
- •2. Линейные операции над векторами и их свойства
- •3. Базис и координаты Декартов прямоугольный базис и декартова система координат
- •Декартова прямоугольная система координат
- •Проекция вектора на ось
- •4. Скалярное произведение векторов
- •Геометрические приложения скалярного произведения векторов в декартовой системе координат
- •5. Векторное произведение векторов
- •6. Смешанное произведение векторов
- •Выражение смешанного произведения в декартовых координатах
- •II. Аналитическая геометрия в пространстве
- •1. Уравнения поверхностей и линий
- •2. Плоскость в пространстве
- •Общее уравнение плоскости (поверхность первого порядка)
- •Неполные уравнения плоскостей
- •Уравнение плоскости «в отрезках»
- •Нормальное уравнение плоскости
- •Расстояние от точки до плоскости
- •Уравнение плоскости, проходящей через три данные точки
- •Угол между двумя плоскостями
- •Условие параллельности и перпендикулярности плоскостей
- •Уравнение прямой, проходящей через две данные точки
- •Угол между двумя прямыми
- •Условие параллельности и перпендикулярности двух прямых
- •4. Прямая и плоскость Точка пересечения прямой и плоскости
- •Уравнение пучка плоскостей, проходящих через прямую
- •III. Аналитическая геометрия на плоскости
- •2. Прямая линия на плоскости
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Окружность
- •Гипербола
- •Сопряженные гиперболы – две гиперболы, которые в одной и той же системе прямоугольных координат при одних и тех же значениях и определяются уравнениями и .
- •Парабола
- •4. Преобразования координат Параллельный перенос
- •Поворот координатных осей
- •Изменение начала координат и поворот осей
- •Приведение общего уравнения кривой второго порядка к каноническому виду
- •5. Линии в полярной системе координат
- •Связь полярных координат с декартовыми
- •Окружности
- •Спирали
- •Астроида
- •IV. ПоверхносТи второго порядка
- •Исследование формы поверхностей второго порядка по их каноническим уравнениям
- •Эллипсоид
- •Гиперболоиды Однополостный гиперболоид
- •Двуполостный гиперболоид
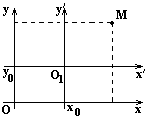
4. Преобразования координат Параллельный перенос
 (1)
(1) 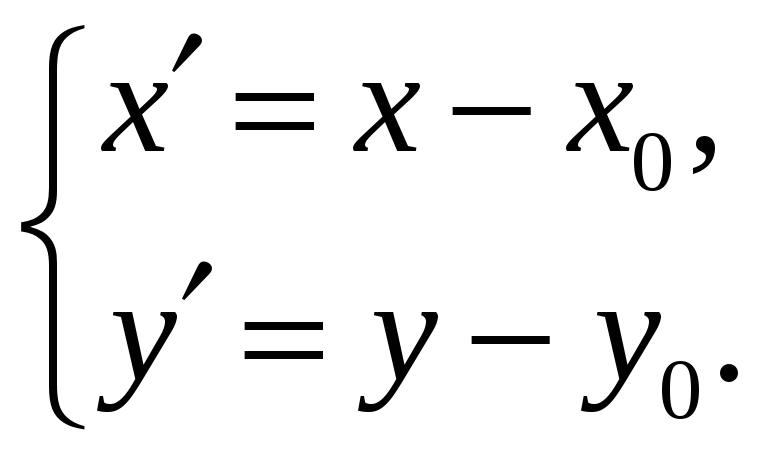 (2)
(2)
Уравнения кривых второго порядка, когда их центры симметрии находятся в точке с координатами O1(x0,y0), получаются с помощью преобразования координат при параллельном переносе осей (2).

![]() - уравнение окружности
с центром
- уравнение окружности
с центром
в точке O1(x0,y0) и радиусом R;
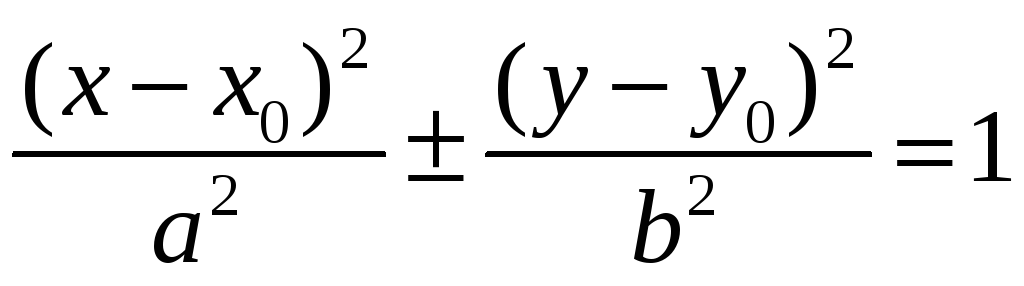 -
уравнения эллипса и гиперболы с
-
уравнения эллипса и гиперболы с
центром симметрии в точке O1(x0,y0);
![]() -
уравнения асимптот гиперболы;
-
уравнения асимптот гиперболы;
![]() -
уравнение параболы с вершиной в точке
O1(x0,y0).
-
уравнение параболы с вершиной в точке
O1(x0,y0).
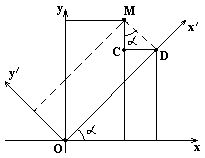
Поворот координатных осей
Выведем формулу преобразования координат при повороте координатных осей.
A B
![]() ,
OD=x,
MD=y.
,
OD=x,
MD=y.
Следовательно, x=OA=OB-AB=OB-CD, y=MA=AC+CM=DB+CM.
Поскольку
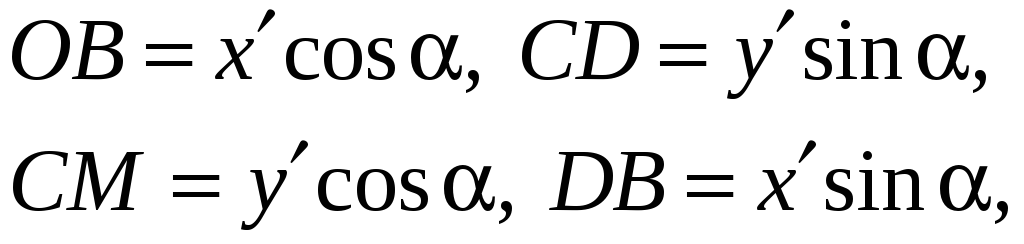
то
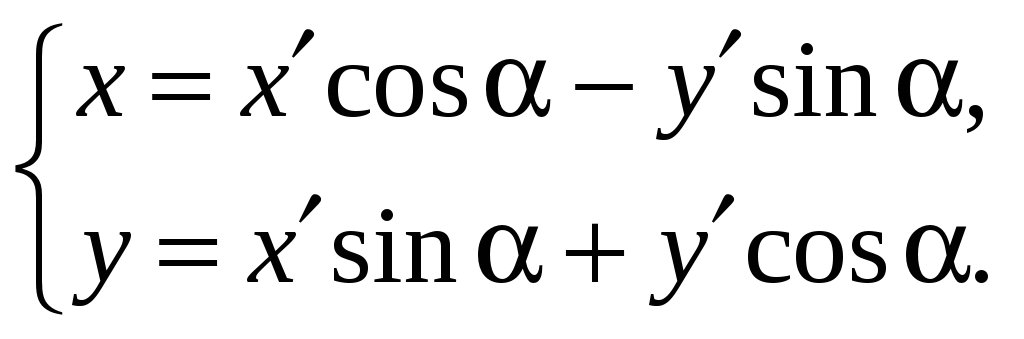 (3)
(3)
Эти формулы выражают старые координаты (x,y) произвольной точки М через новые координаты (x,y) этой же точки при повороте осей на угол .
Формулы, выражающие новые координаты (x,y) точки М через её старые координаты (x,y), получим из следующих соображений: если новая система получена поворотом старой на угол , то старая система получается поворотом новой на угол (-), поэтому в равенствах (3) можно поменять местами старые и новые координаты, заменяя одновременно на (-).
Выполнив это преобразование, получим

Изменение начала координат и поворот осей
Если оси декартовой прямоугольной системы переносятся параллельно на величины x0 по оси ox и на y0 по оси oy и, кроме того, поворачиваются на угол , то этому изменению системы соответствуют формулы преобразования координат, выражающие старые координаты через новые
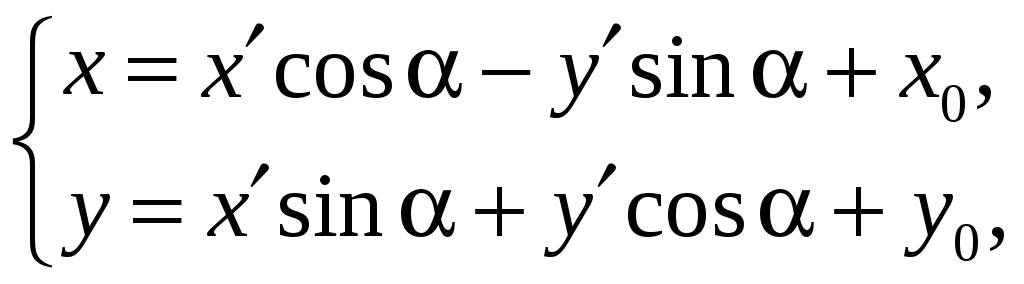 (4)
(4)
и новые координаты через старые:
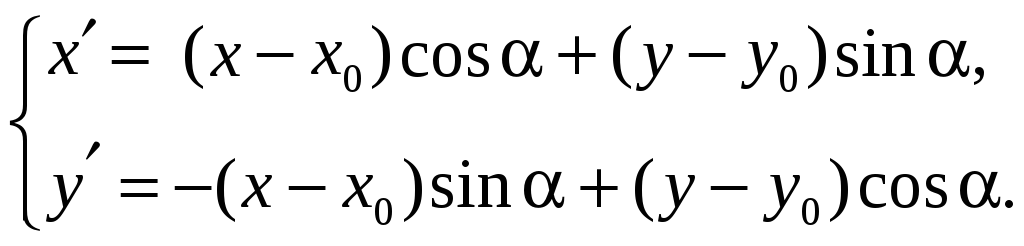 (5)
(5)
Приведение общего уравнения кривой второго порядка к каноническому виду
Пусть кривая второго порядка задана в общем виде:
![]() .
.
Всякая линия второго порядка есть либо эллипс, либо парабола, либо распадается на пару прямых (пересекающихся, параллельных или совпадающих).
Приведение этого уравнения к каноническому виду заключается в нахождении системы координат, в которой кривая имеет канонический вид, геометрически это может быть достигнуто поворотом координатных осей на угол, совмещающий оси симметрии кривой с координатными осями и переносом начала координат в центр кривой (x0,y0).
1)
Члены, содержащие переменные в
первой степени,
исчезают после выделения в общем
уравнении полных квадратов, тем самым
алгебраически позволяют найти центр
кривой после применения формул

Центр кривой, если он существует, находится из системы
 (6)
(6)
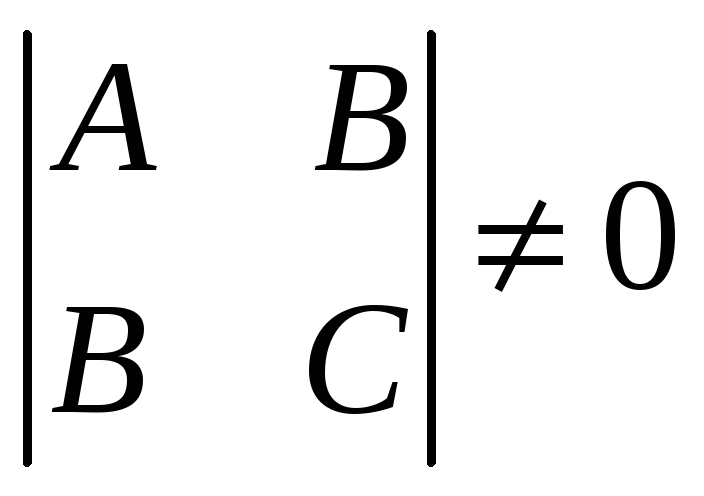 – условие
центральности.
– условие
центральности.
Кривые второго порядка, имеющие единственный центр, называются центральными.
После переноса начала координат в центр (x0,y0) уравнение кривой примет вид
![]() ,
,
где
![]() .
.
2) Члены, содержащие произведение текущих координат исчезают после
применения формул
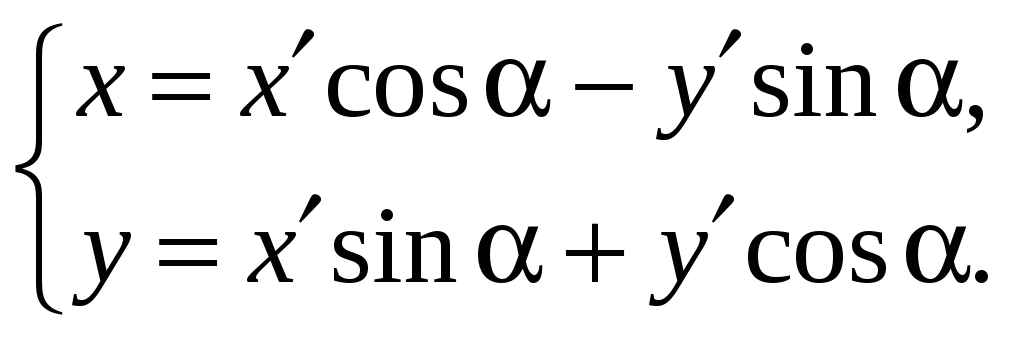
подвергнем
уравнение (6) преобразованию поворота
осей координат на угол
![]() .
.
После преобразования

где
![]() -
новые координаты.
-
новые координаты.
Выпишем из преобразованного уравнения, слагаемые второго порядка:
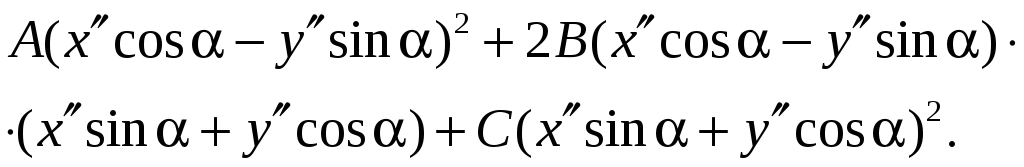
Из
этих слагаемых нас интересует слагаемое,
содержащее произведение
![]() ,
коэффициент перед которым равен
,
коэффициент перед которым равен
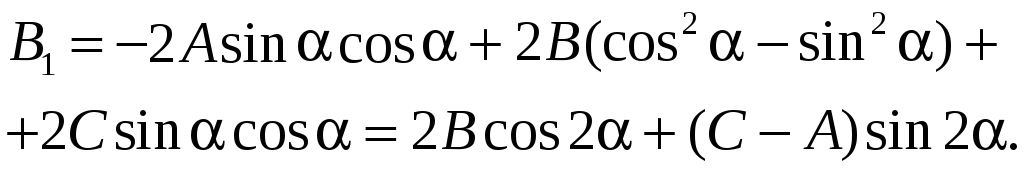
Угол
поворота
находится из условия В1=0:
![]() .
.
Откуда
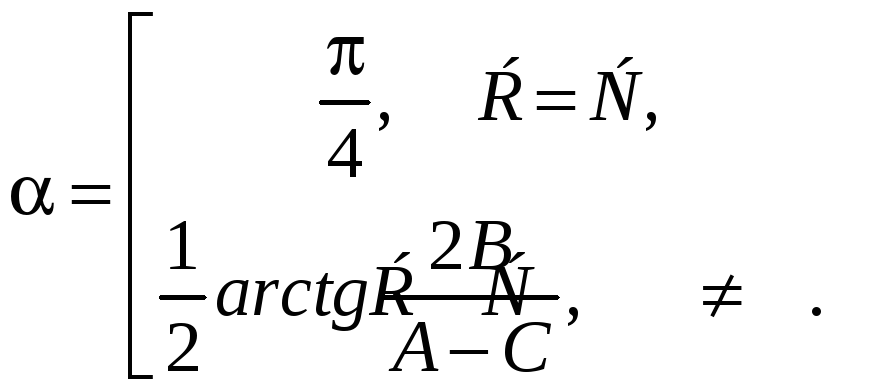 (7)
(7)
Каноническое уравнение кривой принимает вид:
![]() ,
,
где
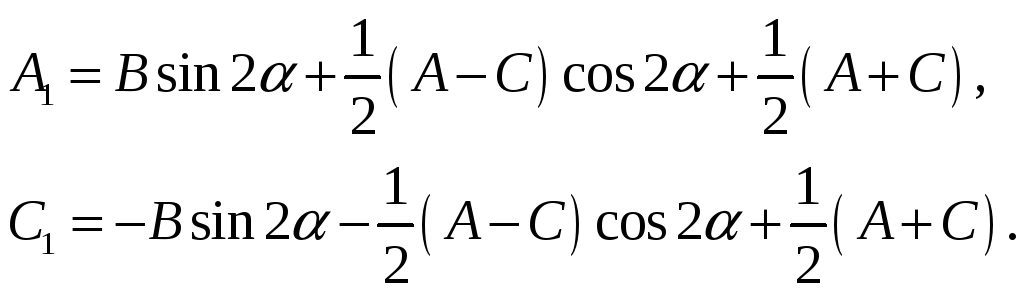
Сделаем некоторые замечания о виде линий второго порядка.
При
переходе от одной системы прямоугольных
координат к другой мы заменяем уравнение
![]()
линии второго порядка другим уравнением
![]() .
.
При
этом выражения
![]() и
и
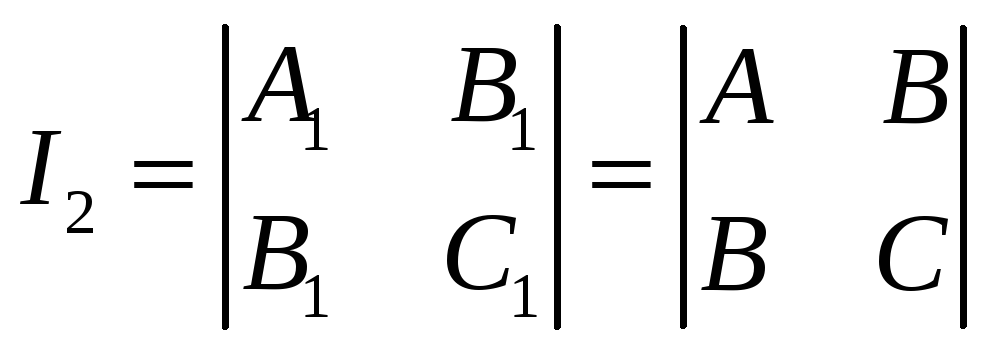
остаются равными. Они называются инвариантами (неизменными) уравнения второй степени.
С их помощью различают три типа линий второго порядка.
-
Эллиптический тип, если
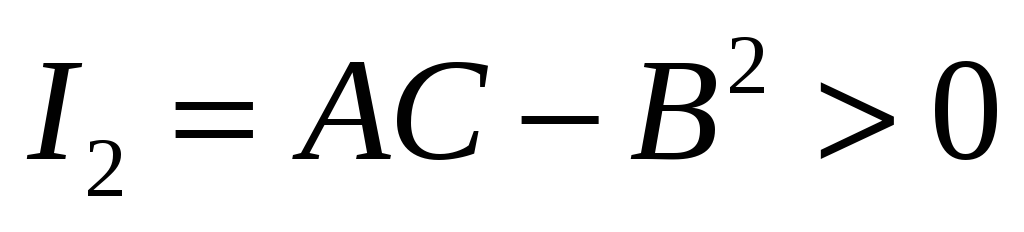 .
.
К нему относятся, кроме действительного эллипса, также мнимый эллипс
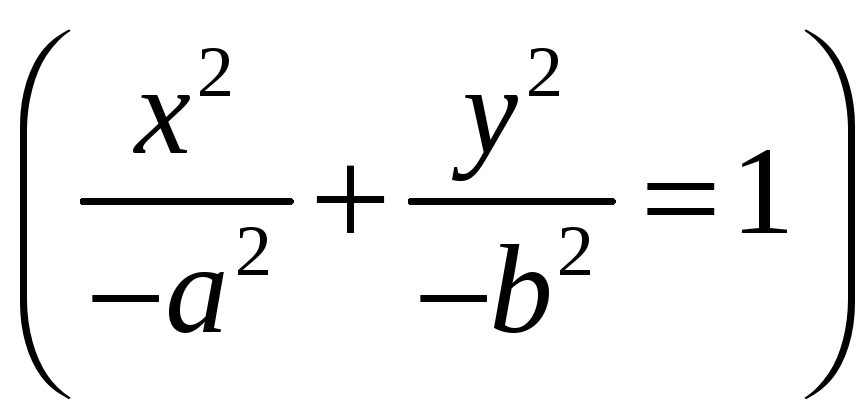
и
пара мнимых прямых, пересекающихся в
действительной точке
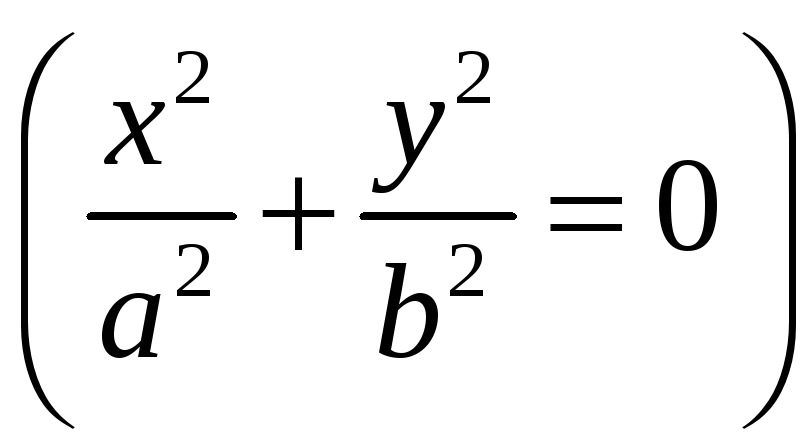 .
.
-
Гиперболический тип, если
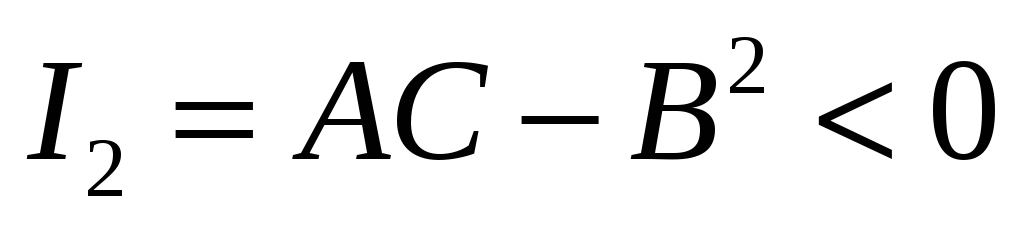 .
.
К
нему относится, кроме гиперболы, пара
действительных пересекающихся прямых
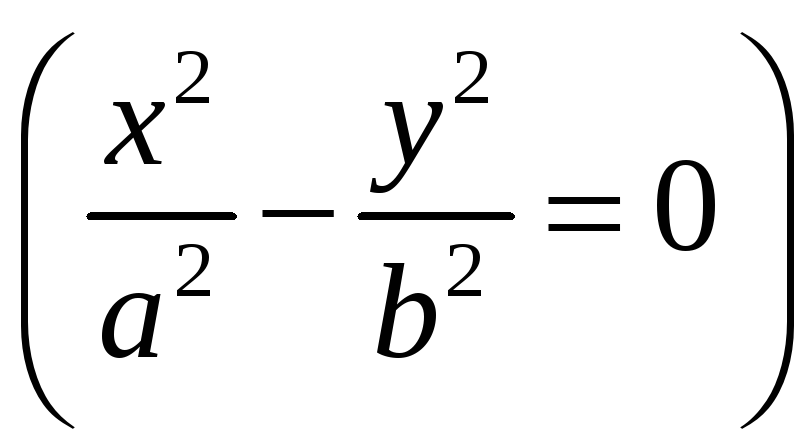 .
.
-
Параболический тип, если
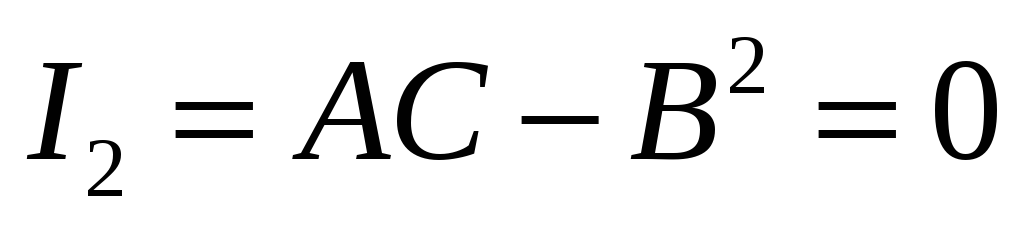 .
.
К нему относится, кроме параболы, пара параллельных (действительных или мнимых) прямых (они могут совпадать).
Пример. Приведите уравнение 5x2 + 9y2 – 30x + 18y + 9 = 0 к каноническому виду и постройте кривую.
Выделим полный квадрат: сгруппируем члены этого уравнения, содержащие одноименные координаты: (5x2 – 30x) + (9y2 + 18y) +9 = 0, 5(x2 – 6x) + 9(y2 + 2y) +9 = 0.
Дополним члены в скобках до полных квадратов: 5(x2 – 6x + 9 – 9) + 9(y2 + 2y + 1 – 1) +9 = 0, 5(x – 3)2 + 9(y + 1)2 = 45.
Введем новые координаты: x = x – 3, y = y + 1, x0 = 3, y0 = -1,
то есть точка О1(3, -1) – центр кривой.
Уравнение в новой системе координат принимает вид:
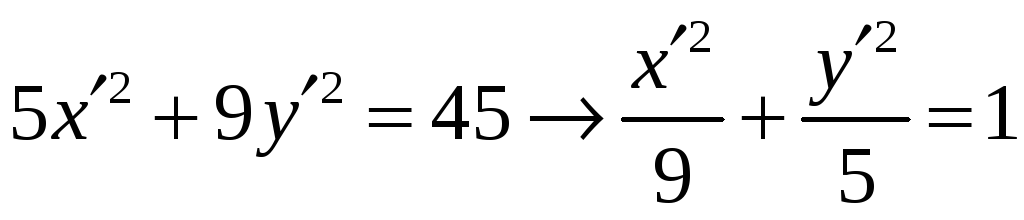 ,
определяет эллипс с полуосями а=3,
b=
,
определяет эллипс с полуосями а=3,
b=![]() который в исходной системе координат
имеет центр в точке О1(3, -1).
который в исходной системе координат
имеет центр в точке О1(3, -1).

Пример.
Определите вид кривой
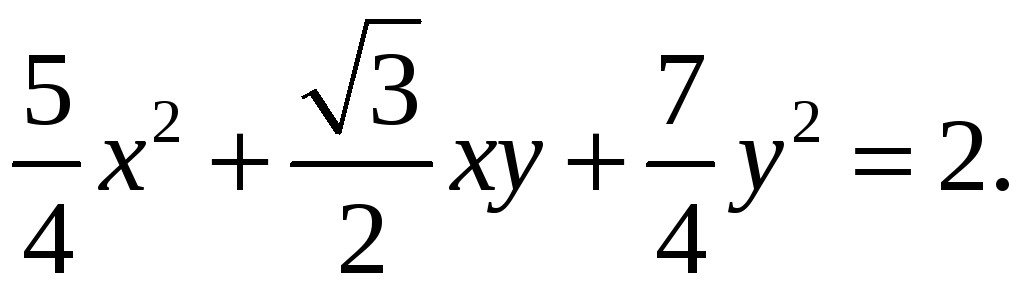
Определим угол поворота осей по формуле (7):
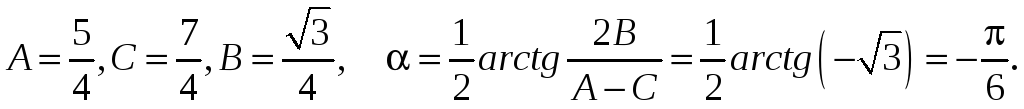
Подвергнем уравнение кривой преобразованию:
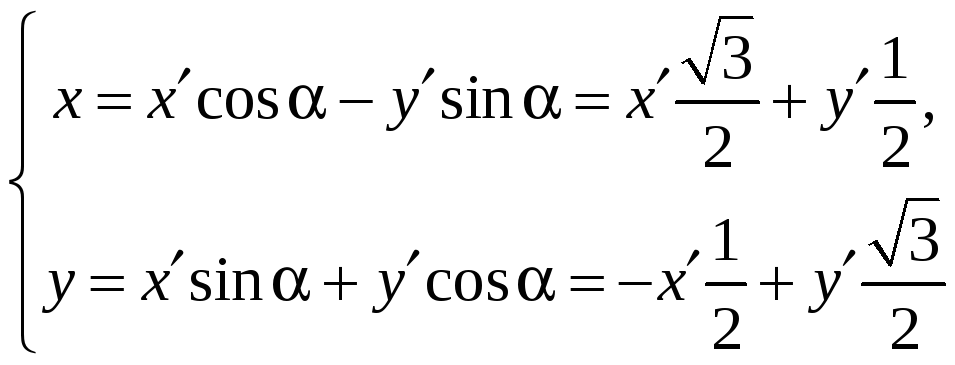
и получим уравнение эллипса
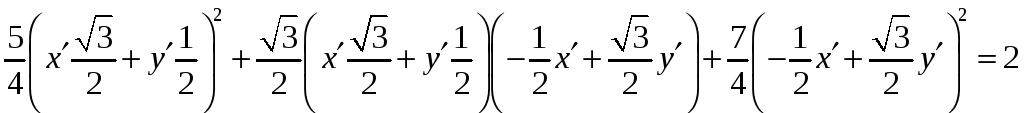 .
.
x 2 + 2y 2 = 2.
