2. Прямая линия на плоскости

Прямая линия – одно из основных понятий геометрии. Если основой построения геометрии служит понятие расстояния между точками, то прямую можно определить как линию, вдоль которой расстояние между двумя точками является кратчайшим.

Уравнения прямой

Общее уравнение прямой на плоскости получается из общего уравнения плоскости в пространстве при z=0:

Ax+By+C=0.

Если А=0 (В=0), то прямая параллельна оси ox (оси oy). Если С=0, то прямая проходит через начало координат.

Если прямая проходит через точку (x₀,y₀) перпендикулярно вектору , ее уравнение принимает вид: .

Каноническое уравнение прямой

Если прямая проходит через точку (x₀,y₀) параллельно направляющему вектору , то получаем каноническое и параметрические уравнения прямой на плоскости в виде:

и

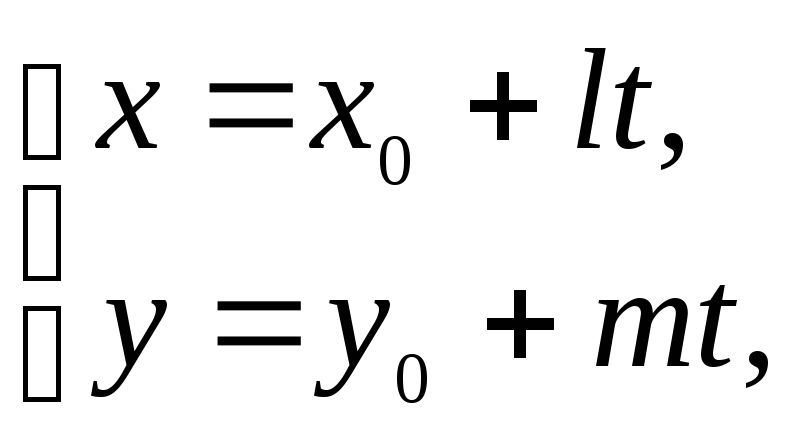
где t - параметр, .

Уравнение прямой, проходящей через две точки

Пусть на плоскости заданы две точки M₁(x₁,y₁), M₂(x₂,y₂). Уравнение прямой, проходящей через эти точки, можно записать как условие коллинеарности векторов , где M(x,y) – произвольная точка прямой. Получаем искомое уравнение в виде

.

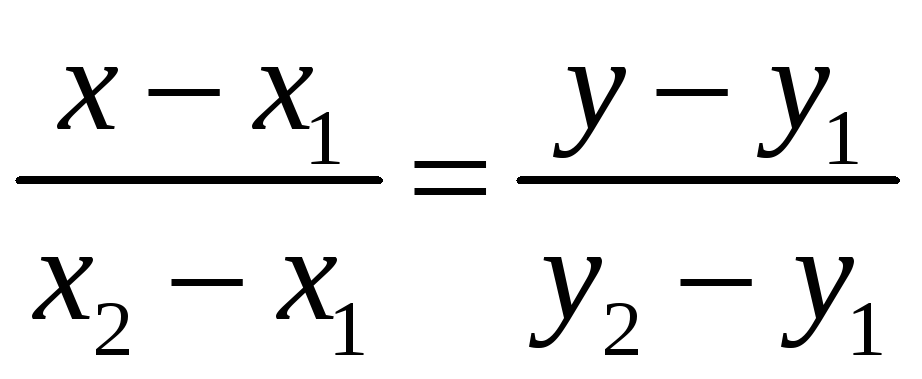Уравнение прямой, проходящей через данную точку в заданном направлении

Пусть прямая составляет угол с осью ох. Угловым коэффициентом прямой k называется число .

Прямая может быть задана точкой М₁(x₁,y₁) и угловым коэффициентом k или двумя точками М₁(x₁,y₁) и М₂(x₂,y₂).

Уравнение прямой с угловым коэффициентом k может быть получено из общего уравнения прямой Ax+By+C=0, если :

, где и .

Прямая пересекает ось oy в точке P(0,b).

Из уравнения прямой, проходящей через две точки, имеем

, ,

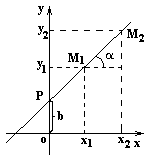
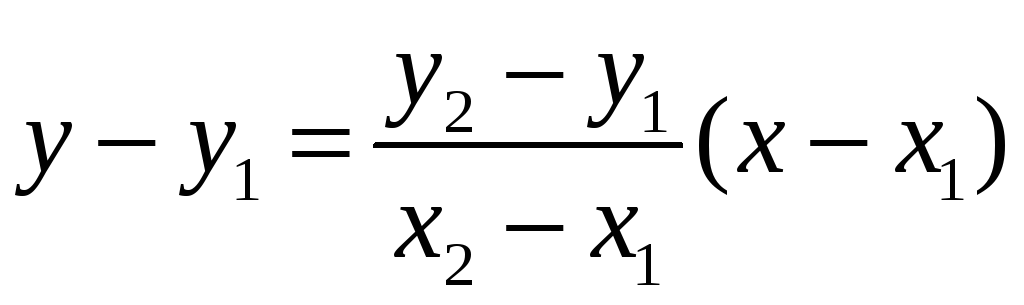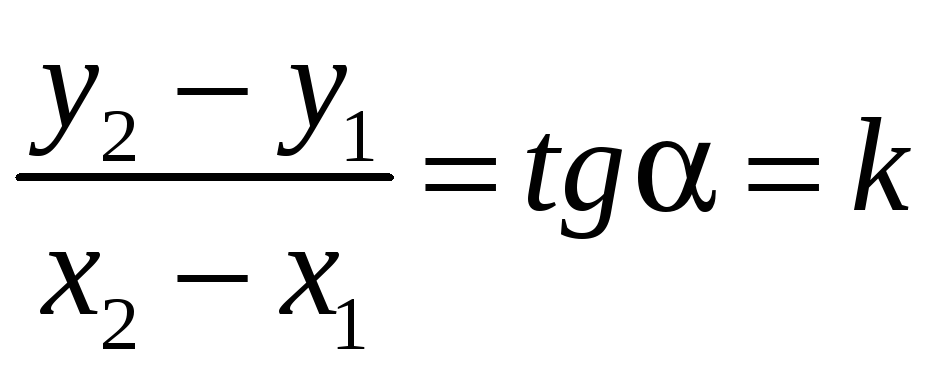Уравнение прямой в отрезках

Общее уравнение прямой Ax+By+C=0 может быть преобразовано к виду уравнения прямой “в отрезках”: .

Прямая в отрезках пересекает ось ox в точке А(а,0) и ось oy в точке В(0,b).

Нормальное уравнение прямой

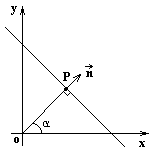
Пусть известно расстояние от прямой до начала координат и угол  между перпендикуляром к прямой и осью OX. Из нормального уравнения плоскости в пространстве, полагая z=0 и учитывая, что

,

получаем нормальное уравнение прямой на плоскости в виде

.

Нормальное уравнение прямой можно получить из общего уравнения прямой Ax+By+C=0, умножив его на нормирующий множитель 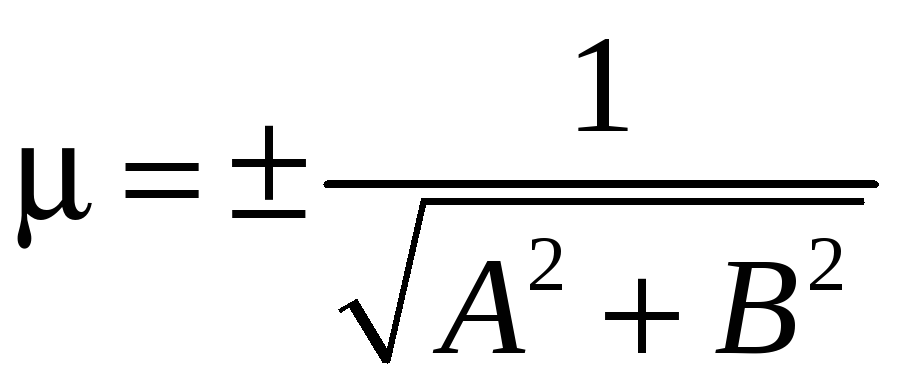. Знак числа  должен быть противоположен знаку числа С.

Косинусы углов, образуемых прямой с осями координат, называются направляющими косинусами прямой.

Если угол между прямой и осью ox равен  и угол между прямой и осью oy равен , то .

Расстояние от точки до прямой

Расстояние d от точки M₀(x₀,y₀) до прямой, задаваемой нормальным уравнением, равно модулю отклонения точки от прямой , d = ||: .

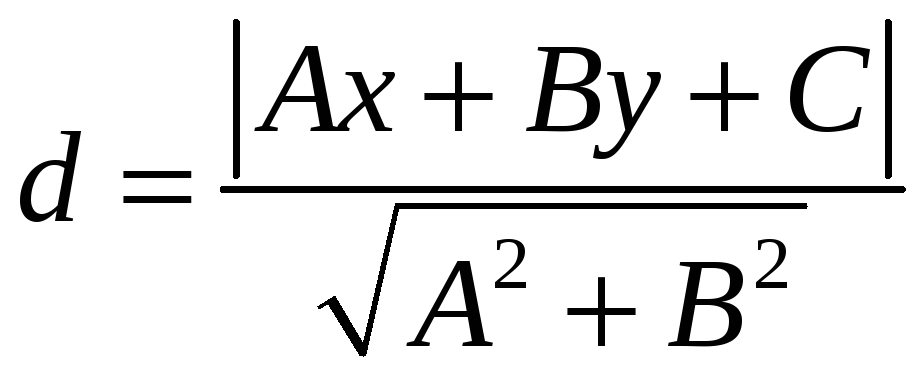По этой формуле положительно, если точка М₀ и начало координат лежат по разные стороны от прямой, в противном случае отрицательно.

Координаты точки пересечения двух прямых

Если прямые заданы уравнениями A₁x+B₁y+C₁=0 и A₂x+B₂y+C₂=0, то координаты точки их пересечения (x₀, y₀) получаются как решение системы уравнений

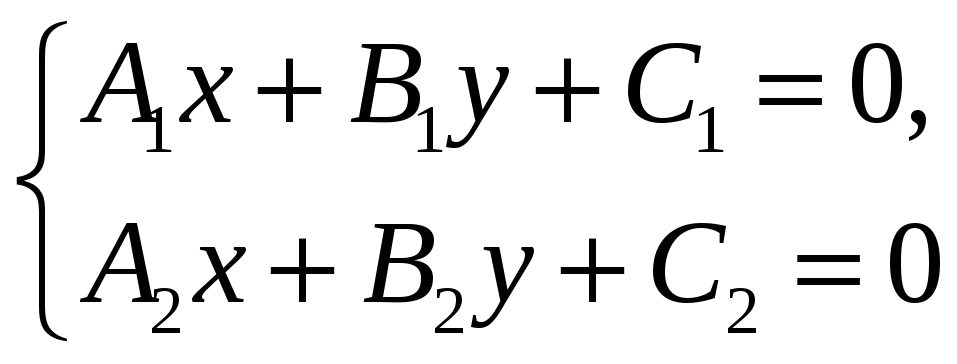
по формулам Крамера в виде 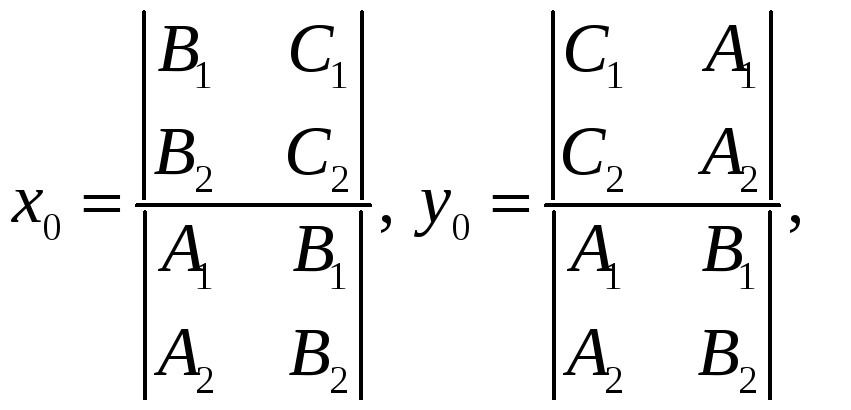при

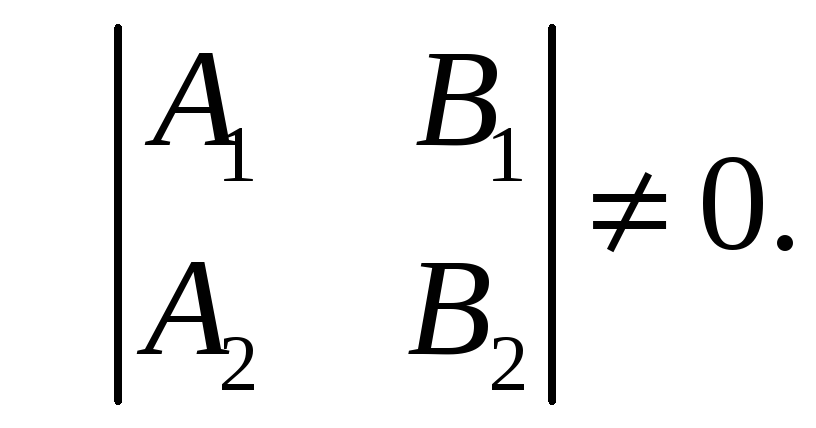
Угол между двумя прямыми

Пусть две прямые заданы уравнениями:

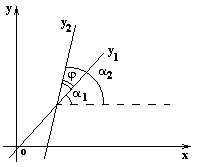
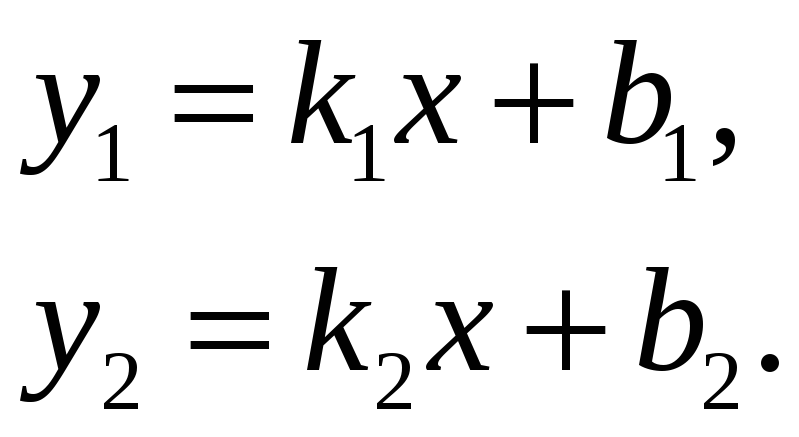
Острый угол  пересечения этих прямых (отсчитываемый против часовой стрелки) находится из следующих соотношений:

.

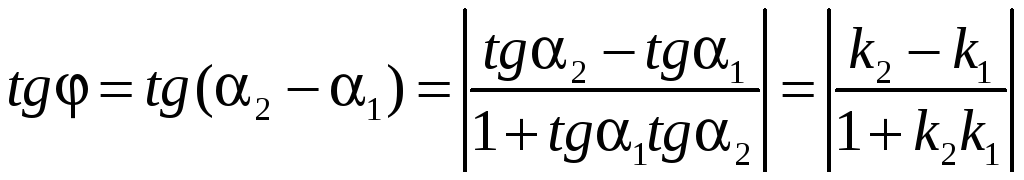Условие параллельности и перпендикулярности двух прямых

Если прямые заданы уравнениями A₁x+B₁y+C₁=0 и A₂x+B₂y+C₂=0, то они параллельны, если 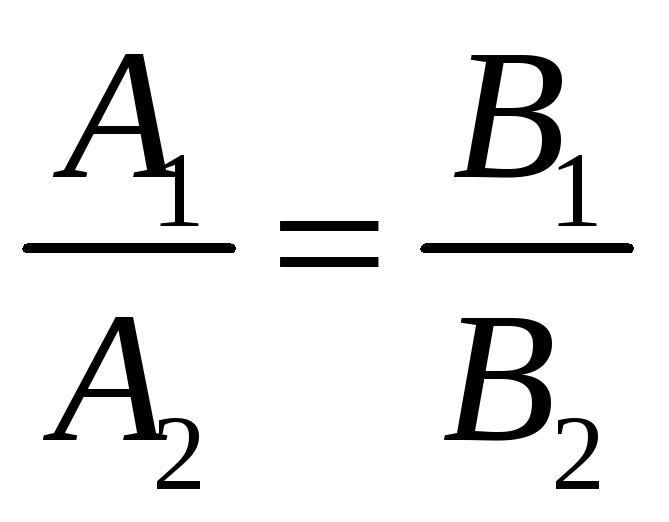, и перпендикулярны, если .

Прямые y₁=k₁x+b₁ и y₂=k₂x+b₂ параллельны друг другу,

если , : k₁=k₂,

и перпендикулярны друг другу, если , : .

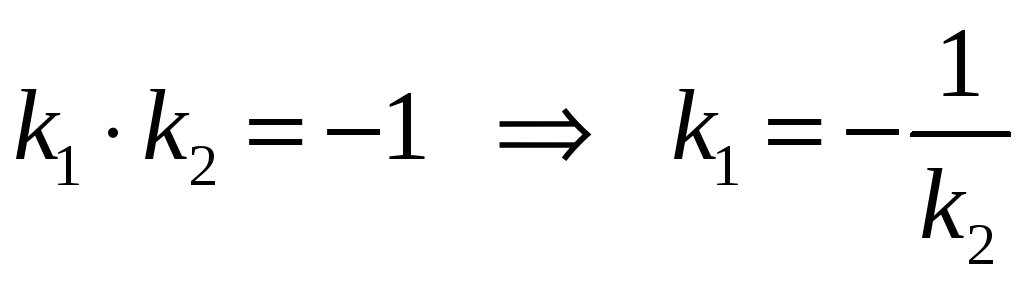3. Кривые второго порядка

Кривые второго порядка на плоскости определяются алгебраическими уравнениями второго порядка.

Эллипс

Эллипсом называется геометрическое место точек M(x,y), для которых сумма расстояний до двух заданных точек F₁(+с,0) и F₂(-с,0) (называемых фокусами эллипса) постоянна и равна 2а.

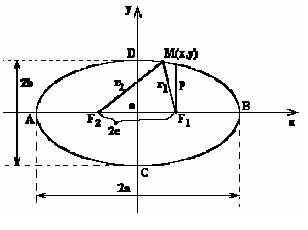
Вывод уравнения эллипса.

По определению и значит а>c.

Воспользуемся формулой расстояния между двумя точками

По определению . Подставим в это равенство r₁ и r₂:

.

Проделаем преобразования:

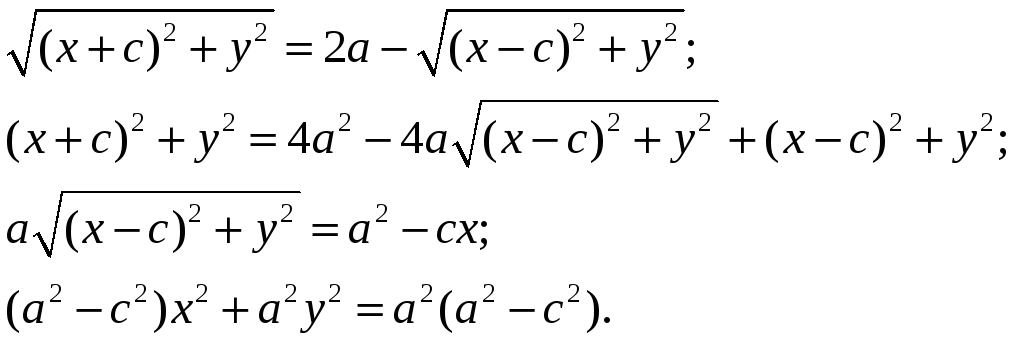
Если a²- c²=b², b²x²+a²y²=a²b² и

- каноническое уравнение эллипса.

Для полноты доказательства следовало показать, что любая точка, удовлетворяющая этому уравнению, принадлежит эллипсу.

Эллипс – центральная линия второго порядка, замкнутая линия, симметричная относительно осей и центра. Элементами эллипса являются: точка О - центр эллипса; точки A, B, C, D - вершины эллипса; точки F₁(с,0), F₂(-с,0) - фокусы эллипса; 2c - фокусное расстояние, которое вычисляется по формуле ; АВ=2а и CD=2b - большая и малая оси эллипса; a и b - большая и малая полуоси эллипса; - эксцентриситет эллипса, который вычисляется по формуле .

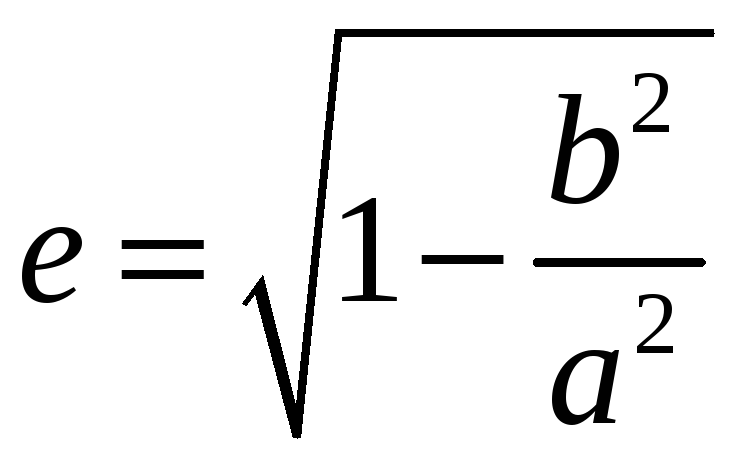Эксцентриситет определяется отношением осей эллипса и характеризует его форму: чем больше e, тем более вытянут эллипс вдоль большой оси.

Прямые и , параллельные малой оси эллипса и отстоящие от его центра на расстояниях , называются директрисами эллипса, соответствующими фокусам F₁ и F₂. Отношение расстояния любой точки эллипса до фокуса к расстоянию ее до соответствующей директрисы постоянно и равно эксцентриситету .