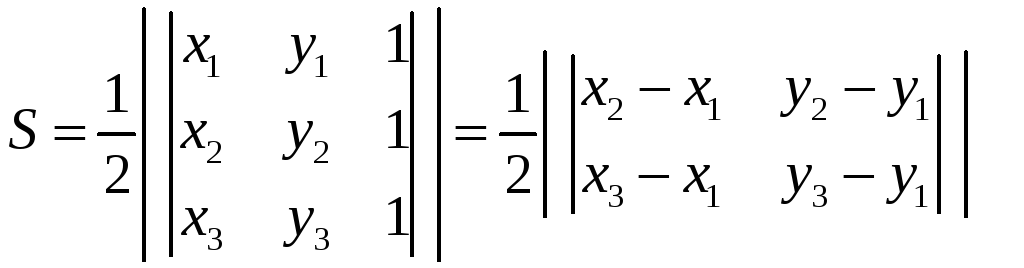- •Оглавление
- •3. Прямая линия в пространстве 22
- •4. Прямая и плоскость 25
- •1. Простейшие задачи на плоскости 26
- •I. Векторная алгебра
- •1. Определение вектора
- •2. Линейные операции над векторами и их свойства
- •3. Базис и координаты Декартов прямоугольный базис и декартова система координат
- •Декартова прямоугольная система координат
- •Проекция вектора на ось
- •4. Скалярное произведение векторов
- •Геометрические приложения скалярного произведения векторов в декартовой системе координат
- •5. Векторное произведение векторов
- •6. Смешанное произведение векторов
- •Выражение смешанного произведения в декартовых координатах
- •II. Аналитическая геометрия в пространстве
- •1. Уравнения поверхностей и линий
- •2. Плоскость в пространстве
- •Общее уравнение плоскости (поверхность первого порядка)
- •Неполные уравнения плоскостей
- •Уравнение плоскости «в отрезках»
- •Нормальное уравнение плоскости
- •Расстояние от точки до плоскости
- •Уравнение плоскости, проходящей через три данные точки
- •Угол между двумя плоскостями
- •Условие параллельности и перпендикулярности плоскостей
- •Уравнение прямой, проходящей через две данные точки
- •Угол между двумя прямыми
- •Условие параллельности и перпендикулярности двух прямых
- •4. Прямая и плоскость Точка пересечения прямой и плоскости
- •Уравнение пучка плоскостей, проходящих через прямую
- •III. Аналитическая геометрия на плоскости
- •2. Прямая линия на плоскости
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Окружность
- •Гипербола
- •Сопряженные гиперболы – две гиперболы, которые в одной и той же системе прямоугольных координат при одних и тех же значениях и определяются уравнениями и .
- •Парабола
- •4. Преобразования координат Параллельный перенос
- •Поворот координатных осей
- •Изменение начала координат и поворот осей
- •Приведение общего уравнения кривой второго порядка к каноническому виду
- •5. Линии в полярной системе координат
- •Связь полярных координат с декартовыми
- •Окружности
- •Спирали
- •Астроида
- •IV. ПоверхносТи второго порядка
- •Исследование формы поверхностей второго порядка по их каноническим уравнениям
- •Эллипсоид
- •Гиперболоиды Однополостный гиперболоид
- •Двуполостный гиперболоид
Уравнение прямой, проходящей через две данные точки
Пусть даны две точки
![]() В качестве направляющего вектора прямой
выберем вектор
В качестве направляющего вектора прямой
выберем вектор
![]() ,
и уравнение прямой, проходящей через
две данные точки примет вид:
,
и уравнение прямой, проходящей через
две данные точки примет вид:
![]()
ПРИМЕР:
Составьте уравнение прямой, проходящей
через две точки
![]()
![]()
![]() .
.
Угол между двумя прямыми
Е сли
сли
![]() и
и
![]() направляющие векторы прямых
направляющие векторы прямых
![]() и
и
![]() ,
то положительное значение косинуса
угла между этими векторами
,
то положительное значение косинуса
угла между этими векторами
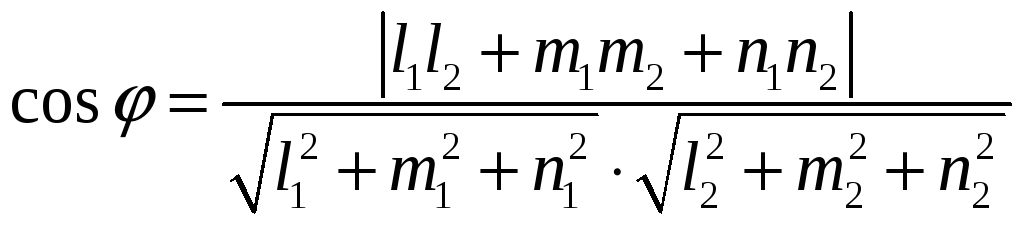
позволяет найти угол между прямыми.
Условие параллельности и перпендикулярности двух прямых
Прямые будут
параллельны,
если их направляющие векторы
![]() параллельны, то есть
параллельны, то есть
![]()
Прямые будут
перпендикулярны,
если их направляющие векторы
перпендикулярны, то есть
![]() .
.
ПРИМЕР: Определите угол между двумя прямыми:
![]()
Находим направляющие
векторы данных прямых. Нормальные
векторы плоскостей, задающих первую
прямую,
![]() ,
и вторую прямую,
,
и вторую прямую,
![]()
Направляющие векторы первой и второй прямых:
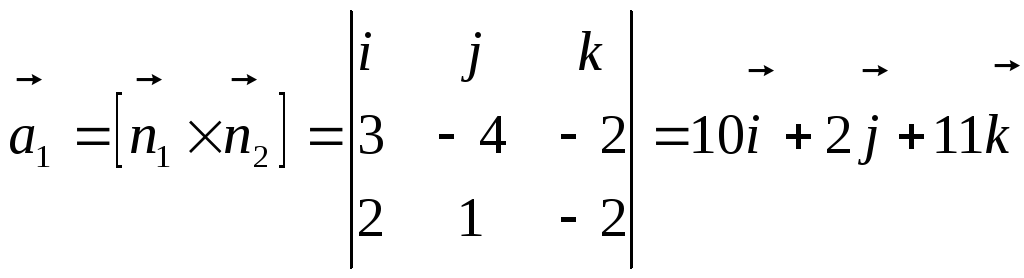 ,
,
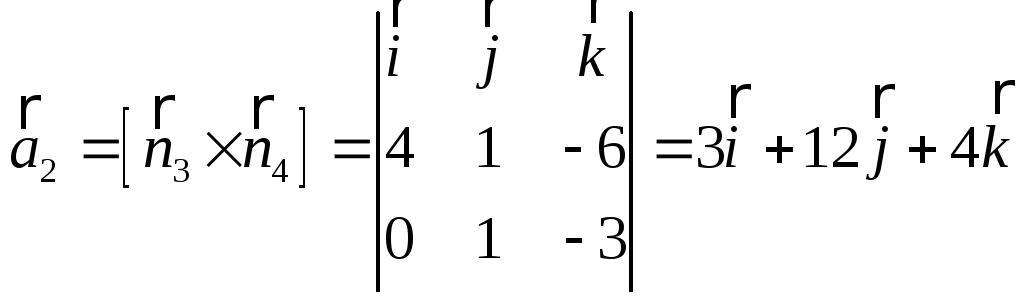 ,
,
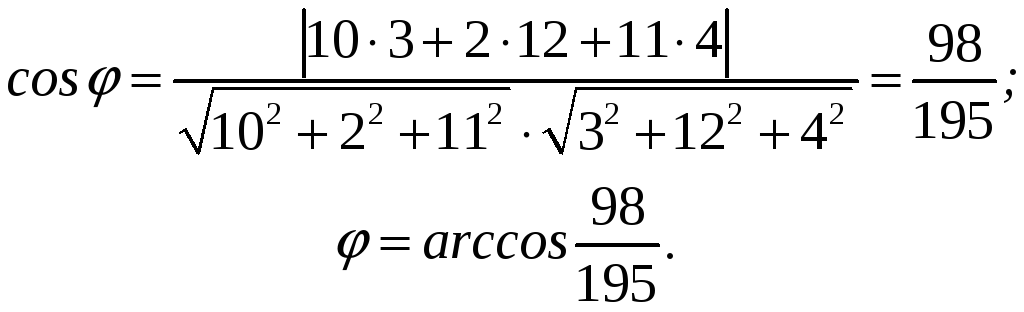
4. Прямая и плоскость Точка пересечения прямой и плоскости
Даны уравнения прямой и плоскости:
![]() .
.
Координаты точки пересечения прямой и плоскости должны одновременно удовлетворять этим уравнениям.
1) Выражая две переменных через третью из уравнений прямой и подставляя их в уравнение плоскости, получим уравнение для одной переменной и найдем точку пересечения прямой и плоскости.
2) Можно перейти к параметрическим уравнениям прямой:
![]() ,
,
тогда подстановка
переменных в уравнение плоскости P,
позволяет найти значение параметра
![]() для координат точки пересечения прямой
и плоскости.
для координат точки пересечения прямой
и плоскости.
3) Если прямая задана общими уравнениями, точка пересечения может быть найдена как решение системы из трех уравнений.
Уравнение пучка плоскостей, проходящих через прямую
Пусть прямая задана линией пересечения двух плоскостей:
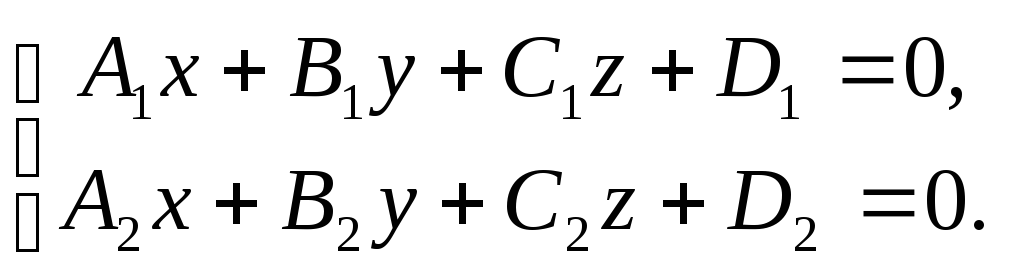
Возьмем любые отличные
от нуля числа
![]() и составим равенство
и составим равенство
![]()
Это равенство
определяет плоскость, которая проходит
через ту же прямую, так как каждая тройка
чисел (x, y, z)
удовлетворяет этим двум равенствам.
Совокупность всех плоскостей, проходящих
через одну и ту же прямую, называется
пучком плоскостей.
Если положить
![]() ,
то уравнение
,
то уравнение
![]()
определяет все плоскости пучка, кроме второй из плоскостей, задающих прямую.
Угол между прямой и плоскостью
У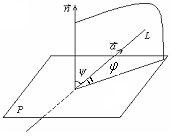 гол
гол
![]() между прямой и плоскостью,
между прямой и плоскостью,
![]()
(![]() – угол между вектором нормали
– угол между вектором нормали
![]() к плоскости и направляющим вектором
к плоскости и направляющим вектором
![]() прямой):
прямой):
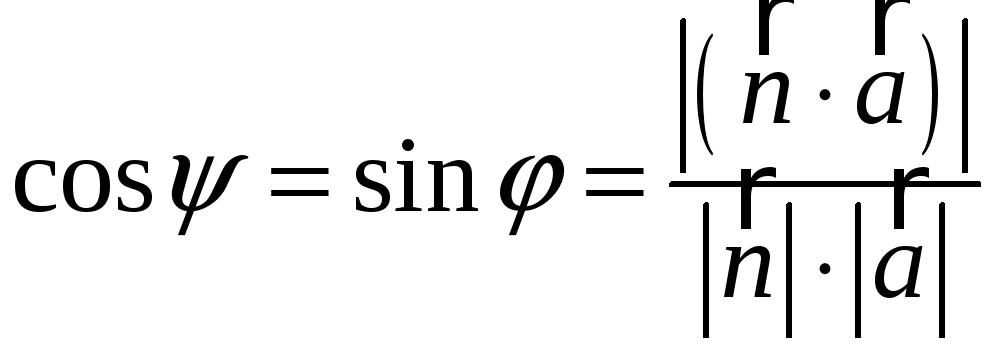 .
.
Условия параллельности и перпендикулярности
прямой
![]() и
и
плоскости
![]()
Прямая L перпендикулярна плоскости P, если направляющий вектор прямой коллинеарен нормальному вектору плоскости, то есть
![]() .
.
Прямая
L параллельна
плоскости P,
если направляющий вектор прямой
перпендикулярен нормальному вектору
плоскости,
![]() то есть
то есть
![]()
III. Аналитическая геометрия на плоскости
1. Простейшие задачи на плоскости
Расстояние между двумя точками
![]() и может быть вычислено по формуле
и может быть вычислено по формуле
![]() .
.
Деление отрезка в данном отношении
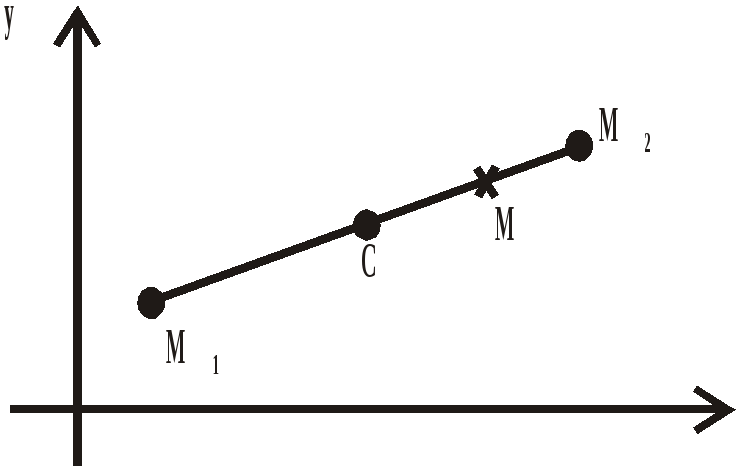
![]() ,
,
если
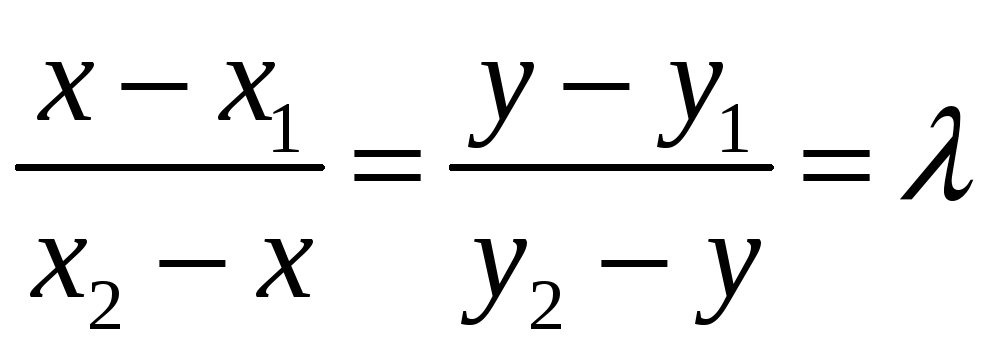 .
.
Координаты
точки М
находятся по формулам
:
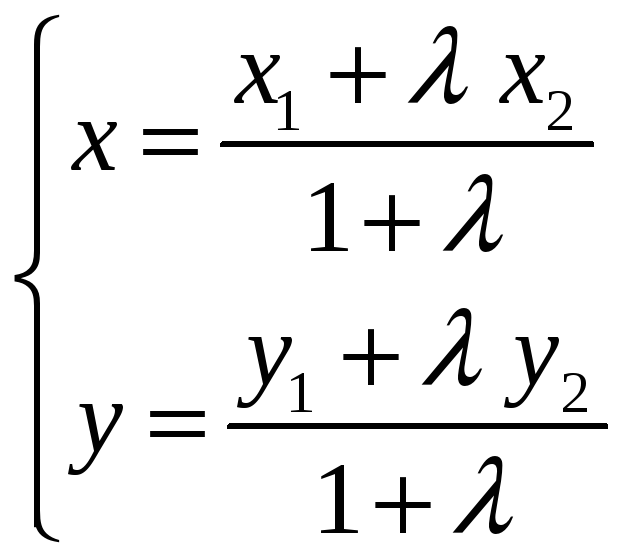
Координаты
середины
отрезка С
получаются при М1М=ММ2,
![]() :
:
![]()
Площадь треугольника
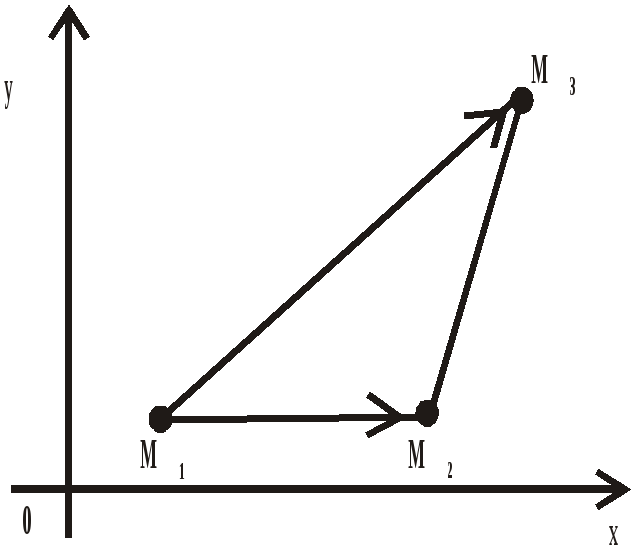
М1(x1,y1), M2(x2,y2), M3(x3,y3).