
- •Оглавление
- •3. Прямая линия в пространстве 22
- •4. Прямая и плоскость 25
- •1. Простейшие задачи на плоскости 26
- •I. Векторная алгебра
- •1. Определение вектора
- •2. Линейные операции над векторами и их свойства
- •3. Базис и координаты Декартов прямоугольный базис и декартова система координат
- •Декартова прямоугольная система координат
- •Проекция вектора на ось
- •4. Скалярное произведение векторов
- •Геометрические приложения скалярного произведения векторов в декартовой системе координат
- •5. Векторное произведение векторов
- •6. Смешанное произведение векторов
- •Выражение смешанного произведения в декартовых координатах
- •II. Аналитическая геометрия в пространстве
- •1. Уравнения поверхностей и линий
- •2. Плоскость в пространстве
- •Общее уравнение плоскости (поверхность первого порядка)
- •Неполные уравнения плоскостей
- •Уравнение плоскости «в отрезках»
- •Нормальное уравнение плоскости
- •Расстояние от точки до плоскости
- •Уравнение плоскости, проходящей через три данные точки
- •Угол между двумя плоскостями
- •Условие параллельности и перпендикулярности плоскостей
- •Уравнение прямой, проходящей через две данные точки
- •Угол между двумя прямыми
- •Условие параллельности и перпендикулярности двух прямых
- •4. Прямая и плоскость Точка пересечения прямой и плоскости
- •Уравнение пучка плоскостей, проходящих через прямую
- •III. Аналитическая геометрия на плоскости
- •2. Прямая линия на плоскости
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Окружность
- •Гипербола
- •Сопряженные гиперболы – две гиперболы, которые в одной и той же системе прямоугольных координат при одних и тех же значениях и определяются уравнениями и .
- •Парабола
- •4. Преобразования координат Параллельный перенос
- •Поворот координатных осей
- •Изменение начала координат и поворот осей
- •Приведение общего уравнения кривой второго порядка к каноническому виду
- •5. Линии в полярной системе координат
- •Связь полярных координат с декартовыми
- •Окружности
- •Спирали
- •Астроида
- •IV. ПоверхносТи второго порядка
- •Исследование формы поверхностей второго порядка по их каноническим уравнениям
- •Эллипсоид
- •Гиперболоиды Однополостный гиперболоид
- •Двуполостный гиперболоид
Окружность
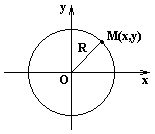
x2+y2=R2.
Гипербола
Гиперболой называется геометрическое место точек M(x,y), для которых абсолютная величина разности расстояний до двух заданных точек F1(+c,0) и F2(-c,0) (называемых фокусами гиперболы) постоянна и равна 2а.
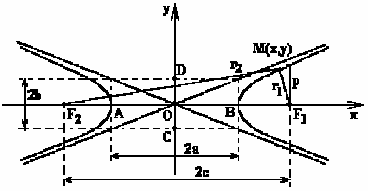
Вывод уравнения гиперболы.
По
определению
![]() и
и
![]() значит а<с.
значит а<с.
Воспользуемся
формулой расстояния между двумя точками
![]()
По
определению
![]() .
Подставим в это равенство r1
и r2:
.
Подставим в это равенство r1
и r2:
![]()
Проделаем преобразования:
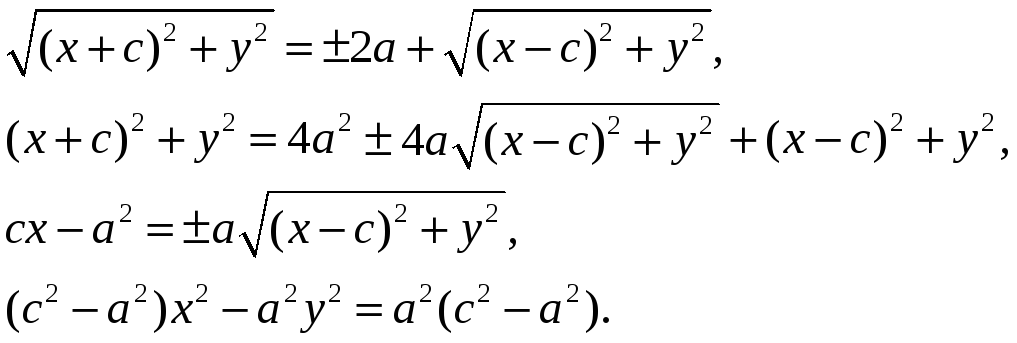
Если c2- a2=b2, то b2x2-a2y2=a2b2 и
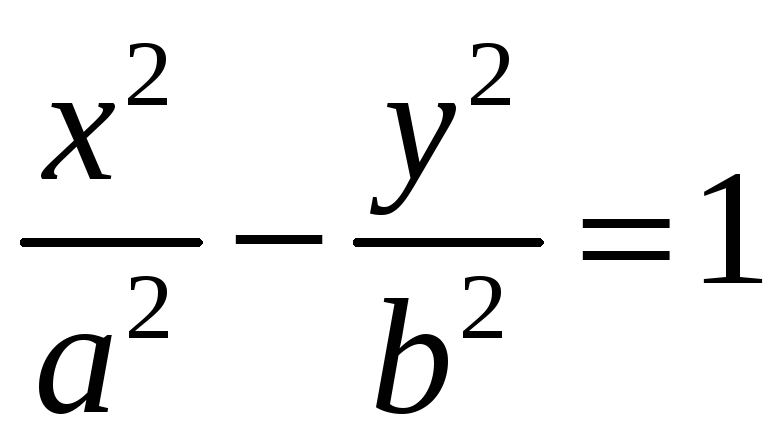 -
каноническое
уравнение гиперболы.
-
каноническое
уравнение гиперболы.
Гипербола
– центральная линия второго порядка.
Она состоит из двух бесконечных ветвей,
симметрична относительно осей. Элементами
гиперболы являются: точка О
- центр
гиперболы; точки А
и В
- вершины
гиперболы; точки F1(+![]() ,0)
и F2(-
,0)
и F2(-![]() ,0)
- фокусы
гиперболы; 2с
- фокусное
расстояние,
которое вычисляется по формуле
,0)
- фокусы
гиперболы; 2с
- фокусное
расстояние,
которое вычисляется по формуле
![]() ;
AB=2a
- действительная
ось гиперболы;
CD=2b
- мнимая ось
гиперболы;
;
AB=2a
- действительная
ось гиперболы;
CD=2b
- мнимая ось
гиперболы;
![]() - эксцентриситет
гиперболы.
- эксцентриситет
гиперболы.
Эксцентриситет определяется отношением осей гиперболы и характеризует еe форму: чем больше e, тем более вытянут вдоль мнимой оси основной прямоугольник гиперболы.
Асимптоты гиперболы - это прямые, к которым ветви гиперболы неограниченно приближаются при удалении в бесконечность.
Уравнения
асимптот гиперболы имеют вид
![]() .
.
Угол
![]() между асимптотами зависит от значения
эксцентриситета гиперболы
между асимптотами зависит от значения
эксцентриситета гиперболы
![]() ,
он определяется из уравнения
,
он определяется из уравнения
![]() .
При
.
При
![]() гипербола называется равнобочной, ее
асимптоты взаимно перпендикулярны,
уравнение гиперболы имеет вид
гипербола называется равнобочной, ее
асимптоты взаимно перпендикулярны,
уравнение гиперболы имеет вид
![]() .
Если принять асимптоты за оси координат,
то уравнение гиперболы примет вид
.
Если принять асимптоты за оси координат,
то уравнение гиперболы примет вид
![]() ,
то есть равнобочная гипербола является
графиком обратной пропорциональности.
,
то есть равнобочная гипербола является
графиком обратной пропорциональности.
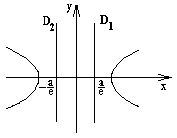 Прямые
Прямые
![]() ,
перпендикулярные действительной оси
гиперболы и отстоящие от ее центра на
расстояниях
,
перпендикулярные действительной оси
гиперболы и отстоящие от ее центра на
расстояниях
![]() ,
называются директрисами
гиперболы, соответствующими фокусам
F1
и F2.
Отношение расстояния любой точки
гиперболы до фокуса к расстоянию ее до
соответствующей директрисы постоянно
и равно эксцентриситету
,
называются директрисами
гиперболы, соответствующими фокусам
F1
и F2.
Отношение расстояния любой точки
гиперболы до фокуса к расстоянию ее до
соответствующей директрисы постоянно
и равно эксцентриситету
![]() .
.
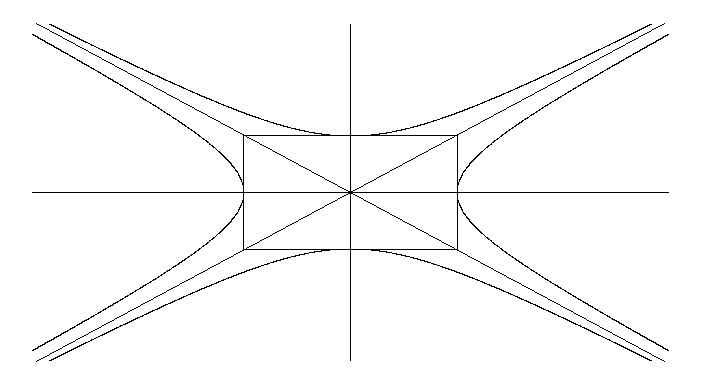
Сопряженные гиперболы – две гиперболы, которые в одной и той же системе прямоугольных координат при одних и тех же значениях и определяются уравнениями и .
Сопряженные гиперболы имеют общие асимптоты. Действительная ось каждой из них есть мнимая ось другой и наоборот.
Парабола
П араболой
называется
геометрическое место точек M(x,y),
расстояние которых до определенной
точки F(p/2,0)
(называемой фокусом
параболы) равно расстоянию до определенной
прямой (называемой директрисой
параболы).
араболой
называется
геометрическое место точек M(x,y),
расстояние которых до определенной
точки F(p/2,0)
(называемой фокусом
параболы) равно расстоянию до определенной
прямой (называемой директрисой
параболы).
Вывод уравнения параболы.
По
определению
![]() и r = d,
и r = d,
![]() .
.
Воспользуемся
формулой расстояния между двумя точками:
![]() ,
,
![]() ,
,
![]() .
.
y2=2px - каноническое уравнение параболы.
Парабола – нецентральная линия второго порядка. Она состоит из одной бесконечной ветви, симметричной относительно оси.
Элементами
параболы являются: точка О
- вершина
параболы; ox
- ось
параболы; точка F(р/2,0)
- фокус
параболы;
![]() - уравнение директрисы
параболы;
- уравнение директрисы
параболы;
![]() - эксцентриситет
параболы, p
- фокальный
параметр
(расстояние от фокуса до директрисы или
половина длины хорды, проходящей через
фокус перпендикулярно оси).
- эксцентриситет
параболы, p
- фокальный
параметр
(расстояние от фокуса до директрисы или
половина длины хорды, проходящей через
фокус перпендикулярно оси).
