- •Оглавление
- •3. Прямая линия в пространстве 22
- •4. Прямая и плоскость 25
- •1. Простейшие задачи на плоскости 26
- •I. Векторная алгебра
- •1. Определение вектора
- •2. Линейные операции над векторами и их свойства
- •3. Базис и координаты Декартов прямоугольный базис и декартова система координат
- •Декартова прямоугольная система координат
- •Проекция вектора на ось
- •4. Скалярное произведение векторов
- •Геометрические приложения скалярного произведения векторов в декартовой системе координат
- •5. Векторное произведение векторов
- •6. Смешанное произведение векторов
- •Выражение смешанного произведения в декартовых координатах
- •II. Аналитическая геометрия в пространстве
- •1. Уравнения поверхностей и линий
- •2. Плоскость в пространстве
- •Общее уравнение плоскости (поверхность первого порядка)
- •Неполные уравнения плоскостей
- •Уравнение плоскости «в отрезках»
- •Нормальное уравнение плоскости
- •Расстояние от точки до плоскости
- •Уравнение плоскости, проходящей через три данные точки
- •Угол между двумя плоскостями
- •Условие параллельности и перпендикулярности плоскостей
- •Уравнение прямой, проходящей через две данные точки
- •Угол между двумя прямыми
- •Условие параллельности и перпендикулярности двух прямых
- •4. Прямая и плоскость Точка пересечения прямой и плоскости
- •Уравнение пучка плоскостей, проходящих через прямую
- •III. Аналитическая геометрия на плоскости
- •2. Прямая линия на плоскости
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Окружность
- •Гипербола
- •Сопряженные гиперболы – две гиперболы, которые в одной и той же системе прямоугольных координат при одних и тех же значениях и определяются уравнениями и .
- •Парабола
- •4. Преобразования координат Параллельный перенос
- •Поворот координатных осей
- •Изменение начала координат и поворот осей
- •Приведение общего уравнения кривой второго порядка к каноническому виду
- •5. Линии в полярной системе координат
- •Связь полярных координат с декартовыми
- •Окружности
- •Спирали
- •Астроида
- •IV. ПоверхносТи второго порядка
- •Исследование формы поверхностей второго порядка по их каноническим уравнениям
- •Эллипсоид
- •Гиперболоиды Однополостный гиперболоид
- •Двуполостный гиперболоид
Расстояние от точки до плоскости
Отклонением точки
![]() от
плоскости называется число, равное
длине перпендикуляра, опущенного из
этой точки на плоскость, взятое со знаком
«-» или «+» в зависимости от того, по одну
или по разные стороны от плоскости
находится начало координат и точка
от
плоскости называется число, равное
длине перпендикуляра, опущенного из
этой точки на плоскость, взятое со знаком
«-» или «+» в зависимости от того, по одну
или по разные стороны от плоскости
находится начало координат и точка![]() .
.
П

![]() .
Спроектируем точку
.
Спроектируем точку
![]() на нормаль к плоскости
на нормаль к плоскости
![]() Отклонение
Отклонение
![]()

то есть, чтобы найти отклонение какой-либо точки от плоскости, нужно в левую часть нормального уравнения этой плоскости подставить координаты точки.
Если плоскость задана
общим уравнением, то отклонение точки
![]() от плоскости
от плоскости
![]() вычисляется по
формуле
вычисляется по
формуле
![]() .
Отклонение положительно, если точка
.
Отклонение положительно, если точка
![]() и
начало координат лежат по разные стороны
от плоскости, и отрицательно, если по
одну сторону.
и
начало координат лежат по разные стороны
от плоскости, и отрицательно, если по
одну сторону.
Расстояние от
точки
![]() до плоскости вычисляется по формуле:
до плоскости вычисляется по формуле:
![]()
![]()
ПРИМЕР:
Найдите расстояние точки M(4,
3, 1) от плоскости
![]() .
.
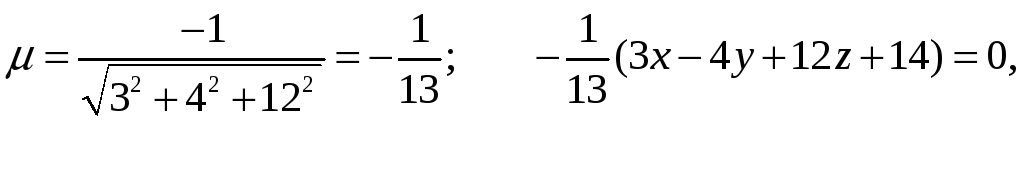
![]()
откуда
![]()
Уравнение плоскости, проходящей через три данные точки
П усть
даны три точки
усть
даны три точки
![]()
![]() .
Введем текущую точку плоскости
.
Введем текущую точку плоскости
![]() и рассмотрим три вектора:
и рассмотрим три вектора:
![]() ,
,
![]() ,
,
![]() .
.
Точка
![]() лежит на плоскости
лежит на плоскости
![]() в том и только в том случае, если эти
векторы компланарны. Условие компланарности
трех векторов определяет плоскость,
проходящую через три данные точки:
в том и только в том случае, если эти
векторы компланарны. Условие компланарности
трех векторов определяет плоскость,
проходящую через три данные точки:

Угол между двумя плоскостями
П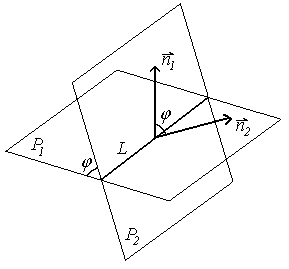 усть
плоскости
усть
плоскости
![]() заданы
уравнениями:
заданы
уравнениями:
![]()
Нормальные векторы этих плоскостей задаются координатами:
![]() .
.
Один из двугранных углов между плоскостями равен острому углу между их нормальными векторами и определяется из равенства
![]()
ПРИМЕР: Найдите
угол между плоскостями
![]()
Нормальные векторы
плоскостей
![]() ,
,![]() .
.
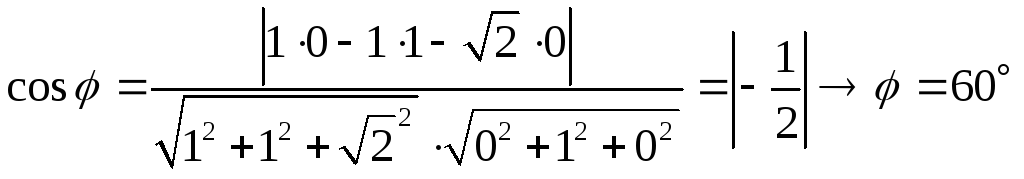 .
.
Условие параллельности и перпендикулярности плоскостей
Плоскости
![]() параллельны,
если их нормальные векторы
параллельны,
если их нормальные векторы
![]() коллинеарны, то есть их координаты
пропорциональны:
коллинеарны, то есть их координаты
пропорциональны:
![]()
Плоскости
![]() перпендикулярны,
если их нормальные векторы перпендикулярны,
перпендикулярны,
если их нормальные векторы перпендикулярны,
![]() :
:
![]() .
.
ПРИМЕР: Составьте уравнение плоскости, которая проходит через точку
M(7, -2, 3) параллельно плоскости y – 3z + 5 = 0.
Нормальные векторы
данной и искомой плоскостей
![]() и
и
![]() .
Из условия параллельности плоскостей:
.
Из условия параллельности плоскостей:
![]() ,
получим A
= 0, B
= 1, C
= - 3 и уравнение искомой плоскости
,
получим A
= 0, B
= 1, C
= - 3 и уравнение искомой плоскости
![]() .
.
ПРИМЕР: Составьте уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям: x – y + 2z – 5 = 0,
2x + y – 3z + 1 = 0.
Нормальные векторы
данных плоскостей:
![]()
![]() .
.
РЕШЕНИЕ 1:
Нормальный вектор искомой плоскости перпендикулярен к нормальным векторам данных плоскостей, т.е.
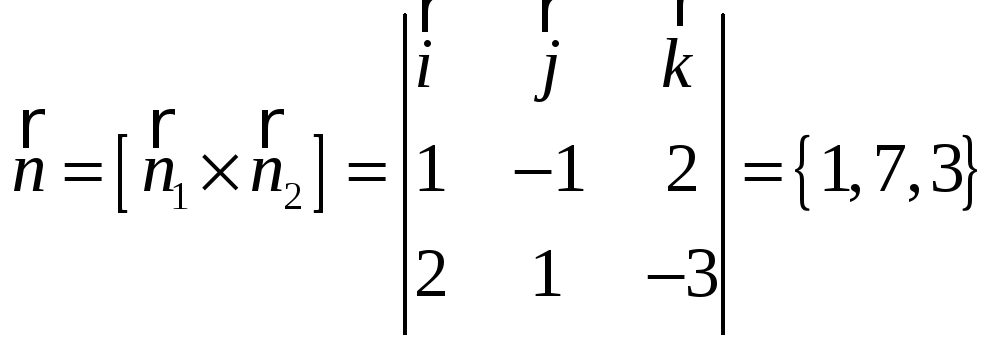
и уравнение искомой плоскости: x + 7y + 3z = 0.
РЕШЕНИЕ 2:
Нормальный вектор
искомой плоскости перпендикулярен к
нормальным векторам данных плоскостей.
Из условия перпендикулярности можно
найти координаты вектора
![]() из системы:
из системы:
 ,
,
3. Прямая линия в пространстве
Общие уравнения прямой
Прямая линия в общем виде определяется как линия пересечения двух плоскостей, то есть системой уравнений:
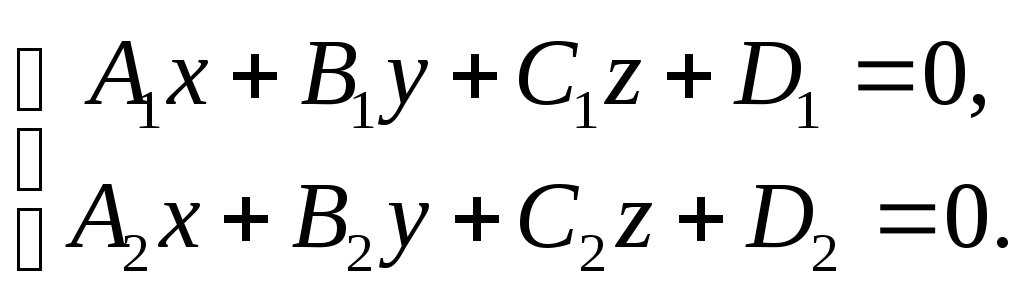
Канонические уравнения прямой
Л юбой
ненулевой вектор
юбой
ненулевой вектор
![]() ,
лежащий на данной прямой или параллельный
ей, называется направляющим
вектором прямой.
,
лежащий на данной прямой или параллельный
ей, называется направляющим
вектором прямой.
Пусть
![]() - текущая точка прямой, а
- текущая точка прямой, а
![]() Вектор
Вектор
![]() коллинеарен вектору
коллинеарен вектору
![]() ,
следовательно, их координаты
пропорциональны.
,
следовательно, их координаты
пропорциональны.
Канонические
уравнения
прямой, проходящей через точку
![]() и
имеющей направляющий вектор
и
имеющей направляющий вектор
![]() ,
имеют вид:
,
имеют вид:
![]()
Параметрические уравнения прямой
Обозначим отношения, входящие в канонические уравнения прямой, через t:
![]() .
.
Отсюда получаем параметрические уравнения прямой в виде:
![]()
Уравнение прямой в виде проекций на координатные плоскости

![]()
ПРИМЕР:
Прямая задана общими уравнениями:![]() (*)
(*)
Составьте канонические и параметрические уравнения прямой. Напишите ее уравнение в виде проекций на координатные плоскости.
Найдем координаты
точки, лежащей на прямой. Положим![]() ,
а две другие координаты найдем из системы
(*):
,
а две другие координаты найдем из системы
(*):
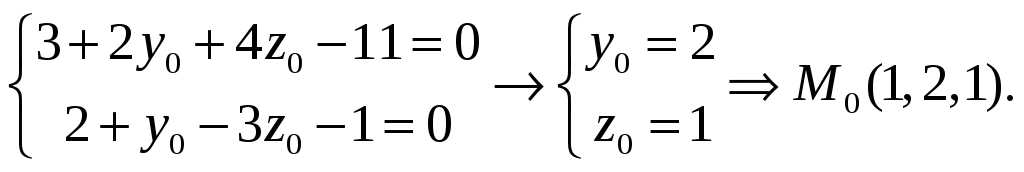
В качестве направляющего вектора прямой выберем вектор, являющийся векторным произведением нормальных векторов плоскостей, линией пересечения которых будет искомая прямая.
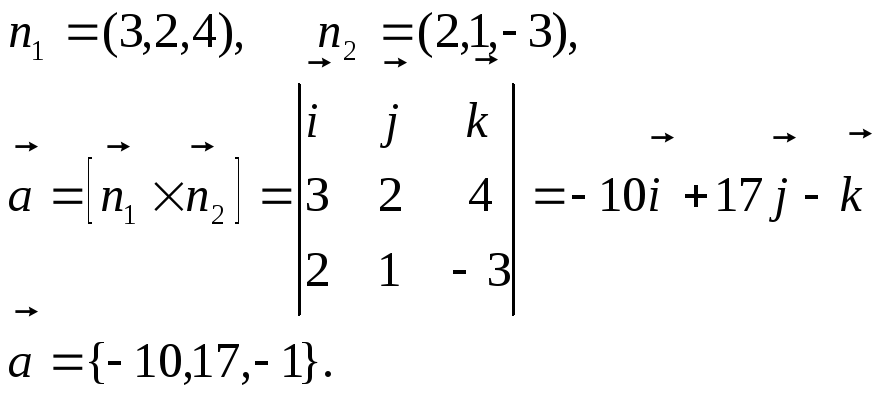 ,
,
Запишем канонические
уравнения прямой:
![]() .
Параметрические уравнения прямой
имеют вид:
.
Параметрические уравнения прямой
имеют вид:
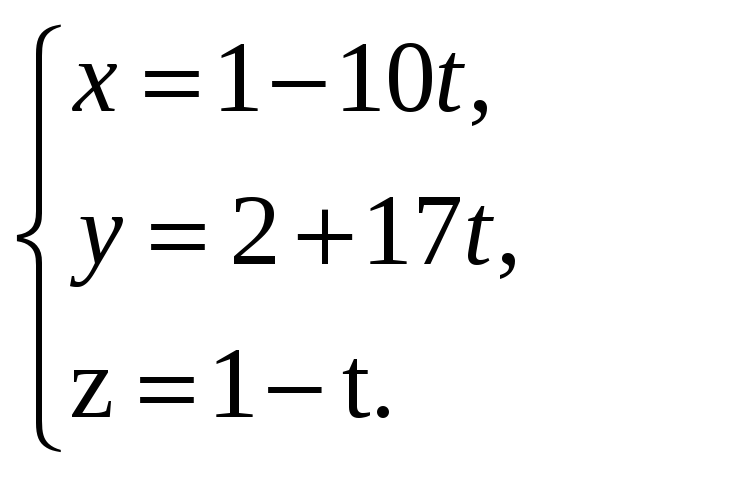
Уравнение прямой в
проекциях: