6. Смешанное произведение векторов

Смешанным произведением векторов , , называется скалярное произведение вектора на векторное произведение векторов и :

.

Смешанное произведение обладает свойствами:

1) ===–=–=–;

2) =0, если или (и) , или (и) =0, или , , компланарны;

смешанное произведение трех векторов, два из которых совпадают, равно нулю;

, если тройка векторов , , – правая,

, если тройка векторов , , – левая.

Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: .

Теорема. Смешанное произведение равно объему параллелепипеда, построенного на приведенных к общему началу векторах , и , взятому со знаком плюс, если тройка правая, и со знаком минус, если тройка левая. Если же векторы , , компланарны, то равно нулю.

Доказательство.

1). Если векторы и коллинеарны, то векторы , и компланарны и .

2). Пусть векторы , неколлинеарны. Построим параллелепипед на векторах , , .

Обозначим через площадь параллелограмма, построенного на векторах и , а через - единичный вектор направления . Тогда , но с точностью до знака равна - высоте параллелепипеда, опущенной из конца вектора на плоскость, определенную векторами и . Очевидно, =, если и лежат по одну сторону от “плоскости векторов и “ и = – , если и лежат по разные стороны от “плоскости векторов и “. Таким образом, при правой ориентации тройки векторов , , и при левой ориентации тройки векторов , , .

Если же векторы , и компланарны, то вектор лежит в плоскости, определенной векторами , = 0.

Выражение смешанного произведения в декартовых координатах

Если три вектора , и заданы своими декартовыми прямоугольными координатами , , , то смешанное произведение равняется определителю, строки которого соответственно равны координатам перемножаемых векторов, т.е., .

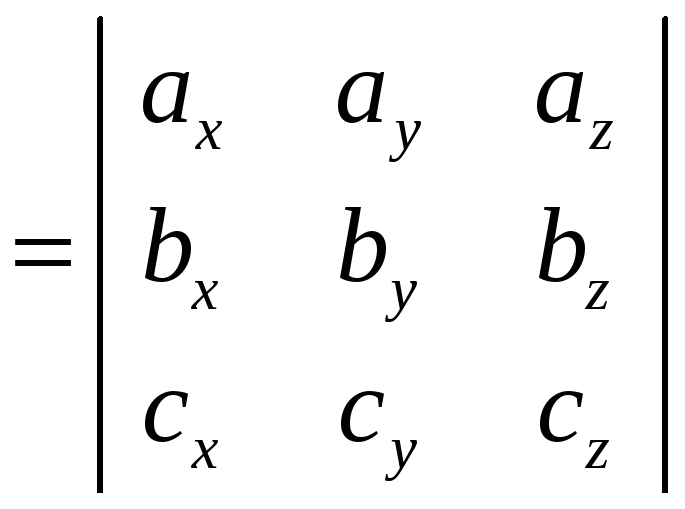Доказательство. Вычислим .

;

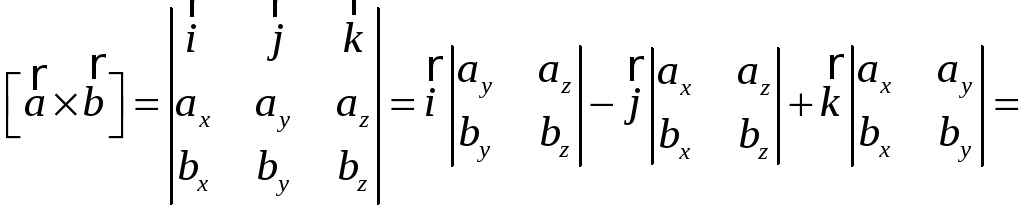
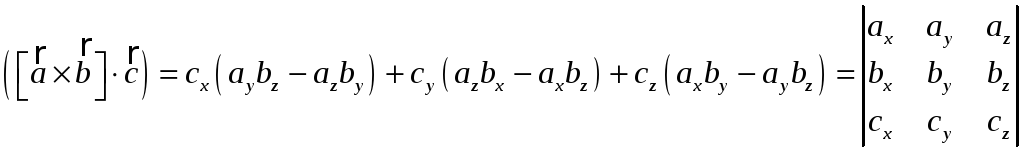
(последнее равенство очевидно, если разложить определитель по элементам третьей строки).

II. Аналитическая геометрия в пространстве

Аналитическая геометрия – раздел геометрии, в котором простейшие геометрические образы (прямые, плоскости, линии и поверхности второго порядка) исследуются средствами алгебры на основе метода координат.

Основная идея метода координат состоит в том, что геометрические свойства образов выясняются путем изучения аналитическими и алгебраическими средствами свойств уравнений геометрических объектов.

1. Уравнения поверхностей и линий

Уравнением поверхности называется такое уравнение, которому удовлетворяют координаты каждой точки, лежащей на этой поверхности, и не удовлетворяют координаты любой точки, не лежащей на ней:

F(x, y, z) = 0.

Геометрическим образом этой зависимости служит поверхность.

Одну из координат в этом уравнении, например z, можно рассматривать как неявную функцию двух других.

Возможно другое, параметрическое выражение функциональной зависимости между несколькими переменными с помощью вспомогательных переменных – параметров. Так, чтобы определить положение точки на поверхности, нужны два параметра, например широта и долгота на поверхности шара. Тогда говорят, что поверхность задана параметрически.

Если уравнения F₁(x, y, z) = 0 и F₂(x, y, z) = 0 являются уравнениями двух поверхностей, пересекающихся по линии L, то линия L есть геометрическое место общих точек этих поверхностей, координаты которых удовлетворяют системе уравнений:

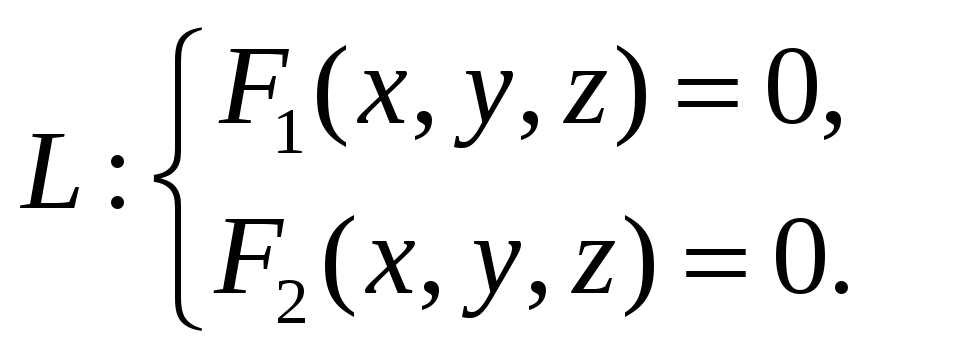
В случае двух переменных зависимость между ними может быть геометрически истолкована как уравнение плоской кривой. Любую величину t,

определяющую положение точки (x, y) на этой кривой, можно принять за параметр. Тогда дадут параметрические уравнения кривой.