
- •Раздел III. Теория вероятностей и математическая статискика Лекция 17. Основные понятия теории вероятностей
- •17.1. Введение. Предмет теории вероятностей
- •17.2. Краткий исторический очерк
- •17.3. Случайное событие. Его частота
- •17. 4. Классическое определение вероятности. Непосредственный подсчет вероятностей.
- •Лекция 18. Алгебра событий. Основные теоремы теории вероятностей
- •18.1. Алгебра событий
- •18.2. Теорема сложения вероятностей
- •18.3. Полная группа событий. Противоположные события
- •18.4. Теорема умножения вероятностей Независимые и зависимые события.
- •18.5. Теорема умножения вероятностей независимых событий
- •18.6. Условная вероятность
- •18.7. Теорема умножения вероятностей зависимых событий
- •Лекция 19. Основные теоремы теории вероятностей (продолжение)
- •19.1. Теорема сложения вероятностей совместных событий
- •19. 2. Формула полной вероятности
- •19.3. Формулы Бейеса (формулы переоценки вероятностей гипотез)
- •19. 4. Повторение испытаний. Формула Бернулли
- •Лекция 20. Случайные величины и их законы распределения
- •20.1. Дискретные и непрерывные случайные величины
- •Понятие закона распределения вероятностей дискретной случайной величины
- •20. 3. Биноминальное распределение
- •20. 4. Распределение Пуассона
- •20. 5. Простейший пуассоновский поток событий
- •21.2. Математическое ожидание и его основные свойства
- •21.3. Дисперсия дискретной случайной величины
- •21.4. Среднее квадратическое отклонение
- •21.5. Свойства дисперсии
- •21. 6. Понятие о моментах распределения
- •21.7. Определение интегральной функции распределения
- •21.8. Свойство интегральной функции
- •21.9. График интегральной функции
- •22.2. Вероятность попадания непрерывной случайной
- •22.3. Нахождение интегральной функции распределения по известной дифференциальной
- •22.4. Свойства дифференциальной функции. Ее вероятностный смысл
- •22.5. Математическое ожидание. Дисперсия. Среднее квадратическое отклонение
- •22.6. Начальные и центральные моменты
- •22.7. Коэффициент асимметрии
- •22.8. Эксцесс
- •22.9. Мода. Медиана
- •Лекция 23. Законы распределения непрерывной случайной величины
- •Закон равномерного распределения или закон равномерной плотности
- •23.2. Нормальное распределение
- •23.3. Вероятность попадания случайной величины, подчиненной нормальному закону, на интервал [
- •23.4. Правило трех сигм
- •Лекция 24. Система случайных величин
- •24.1. Понятие о системе случайных величин
- •24.2. Закон распределения вероятностей дискретной двумерной случайной величины
- •24.3. Интегральная и дифференциальная функция распределения двумерной случайной величины и их свойства
- •24.4. Условные законы распределения составляющих системы дискретных случайных величин
- •24.5. Числовые характеристики системы двух случайных величин
- •24.6. Коррелированность и зависимость случайных величин
- •Лекция 25. Предельные теоремы
- •25.1. Закон больших чисел
- •25.2. Теорема Чебышева
- •25.3. Теорема Бернулли
- •25.4. Центральная предельная теорема
22.2. Вероятность попадания непрерывной случайной
величины в заданный интервал
Теорема. Вероятность того, что непрерывная случайная величина примет значения, принадлежащие интервалу [a, b], равна определенному интегралу от дифференциальной функции, взятому в пределах от а до b:
Р (a<X<b)=![]()
Доказательство: Ранее доказали, что
Р (a X<b)=F(b)–F(a).
По формуле Ньютона
- Лейбница
F(b)–F(a)=![]() =
=
![]()
известно также, что Р (a X<b)=Р (a<X<b)
Следовательно,
Р (a<X<b)=![]() (22.1)
(22.1)
Что и требовалось доказать.
Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее - интервалу [a, b], равно площади криволинейной функции распределения, осью ОХ, прямыми х=а, х=b (рис. 22.1).

Рис. 22.1
22.3. Нахождение интегральной функции распределения по известной дифференциальной
Зная дифференциальную
функцию f(х),
можно найти интегральную функцию F(х)
по формуле: F(х)=![]()
Действительно, F(х)=Р (Х<х), или, F(х)=Р (-<Х<х).
По формуле (22.1.) предыдущего раздела приняв а=-, b=х, получим:
Р (-<Х<х)=![]() ,
или F(х)=
,
или F(х)=![]()
Геометрически связь f(х) и F(х) можно пояснить рисунком 22.2.

Рис. 22.2.
Пример. Найти
интегральную функцию по данной
дифференциальной функции:

Определить Р(2<Х<3).
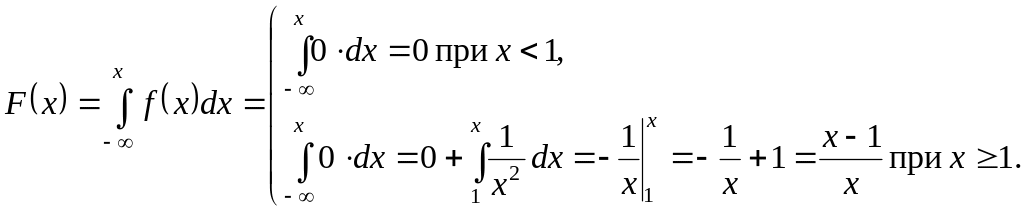
Р (2<Х<3)=![]() ,
или через интегральную функцию Р
(2<Х<3)=F(3)–F(2)=
,
или через интегральную функцию Р
(2<Х<3)=F(3)–F(2)=![]()
![]()

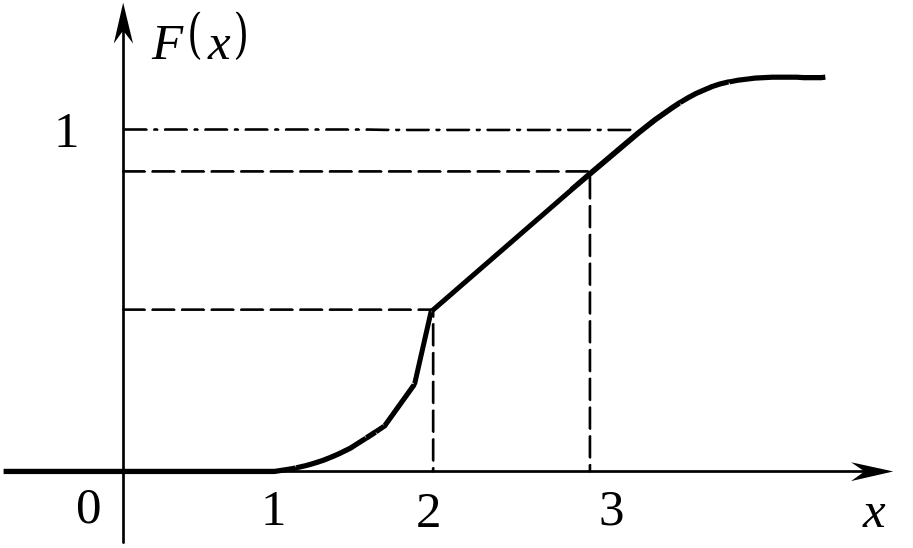
Замечание. График дифференциальной функции называют кривой распределения.
22.4. Свойства дифференциальной функции. Ее вероятностный смысл
Свойство 1. Дифференциальная функция неотрицательная f(х) 0
Доказательство.
Интегральная
функция F(х)
-неубывающая,
т.е.
![]() Но F`(х)=f(х),
т.е. f(х)
0.
Но F`(х)=f(х),
т.е. f(х)
0.
Свойство 2.
Несобственный
интеграл от дифференциальной функции
в пределах от -
до +
равен единице:
![]()
Доказательство.
![]() выражает собой вероятность того, что
случайная величина примет значение в
интервале
выражает собой вероятность того, что
случайная величина примет значение в
интервале
![]() .
Такое событие достоверно, и его вероятность
равна 1. Что и требовалось доказать.
.
Такое событие достоверно, и его вероятность
равна 1. Что и требовалось доказать.
Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью Ох и дифференциальной кривой распределения, равна 1.
В частности, если
все возможные значения случайной
величины, расположены на,
![]() то
то
![]() =1.
=1.
Рассмотрим
вероятностный смысл дифференциальной
функции распределения f(х)=F`(х),
т.е. f(х)=![]() F(x+x)–F(x)
- вероятность, того, что х<X<x+х.
F(x+x)–F(x)
- вероятность, того, что х<X<x+х.
По аналогии с определением плотности массы в точке значения функции f(х) можно рассматривать как плотность вероятности в этой точке.
Если масса непрерывно
распределена вдоль оси Ох по закону
F(х),
плотностью массы р(х)
в точке х
называют
![]() =
р(х)
=
р(х)
Поэтому часто, вместо термина «дифференциальная функция распределения», употребляют термин «плотность вероятности».
Т.к. х=dx и F`(x)=f(x), то можно записать F(х+x)–F(x) f(x)dx.
Вероятностный
смысл этого неравенства таков: вероятность
того, что случайная величина примет
значение, принадлежащее интервалу
![]() ,
приближенно равна (с точностью до
бесконечно малых низшего порядка
относительно
х)
площади прямоугольника с основанием
х
и высотой f(х)
(рис. 22.3).
,
приближенно равна (с точностью до
бесконечно малых низшего порядка
относительно
х)
площади прямоугольника с основанием
х
и высотой f(х)
(рис. 22.3).

Рис. 22.3
